Гідність цих методів полягає в тому, що вони зводять рішення крайової задачі для диференціального рівняння до вирішення системи алгебраїчних рівнянь щодо значень шуканої функції на заданій множині точок. Це досягається заміною похідних, що входять в диференціальне рівняння, їх кінцево-різницевими апроксимаціями.
Розглянемо сутність такого методу вирішення для диференціального рівняння другого порядку (1.41) при заданих граничних умовах (1.42). Розіб'ємо відрізок [0,1] на n рівних частин точками xi = ih (i = 0,1. N). Рішення крайової задачі (1.41), (1.42) зведемо до обчислення значень сіткової функції yi в вузлових точках xi. Для цього напишемо рівняння (1.42) для внутрішніх вузлів:
Замінимо похідні, що входять в ці співвідношення, їх кінцево-різницевими апроксимаціями:
Підставляючи ці вирази в (1.49), отримуємо систему різницевих рівнянь:
що є системою n -1 алгебраїчних рівнянь щодо значень сіткової функції Вхідні в дану систему y 0 (при i = 1) і уп (при i = п - 1) беруть з граничних умов (1.42):
На практиці часто граничні умови задають в більш загальному вигляді (1.38):
В цьому випадку граничні умови також повинні представлятися в різницевої вигляді шляхом апроксимації похідних Y '(0) і Y' (1) за допомогою кінцево-різницевих співвідношень. Якщо використовувати односторонні різниці (відповідний шаблон показаний на рис. 1.7, а), при яких похідні апроксимуються з першим порядком точності, то різницеві граничні умови візьмуть вид
З цих співвідношень легко знаходяться значення y 0, yn.
Однак, як правило, краще апроксимувати похідні, що входять в (1.52), з другим порядком точності за допомогою центральних різниць:
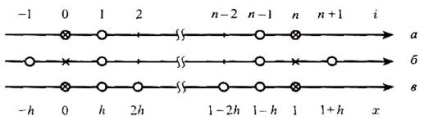
Мал. 1.7. Апроксимація граничних умов
В дані вирази входять значення сіткової функції і yn + 1 в так званих фіктивних вузлах х = 1-h і x = 1 + h, що лежать поза розглянутого відрізка (рис. 1.7, б). У цих вузлах значення шуканої функції також повинні бути знайдені. Отже, кількість невідомих значень сіткової функції збільшується на два. Для замикання системи залучають ще два різницевих рівняння (1.51) при i = 0, i = п.
Апроксимувати граничні умови з другим порядком можна й інакше (див. Рис. 1.7, в). У цьому випадку використовують апроксимації:
Таким чином, рішення крайової задачі для диференціального рівняння зведено до розв'язання системи алгебраїчних рівнянь виду (1.51). Ця система є лінійною або нелінійною в залежності від того, лінійно або нелінійно диференціальне рівняння (1.41). Методи вирішення таких систем розглянуто раніше.
з граничними умовами виду
Розіб'ємо відрізок [0,1] на частини з постійним кроком hс допомогою вузлів. Апроксимуємо другу похідну Y² кінцево-різницевим співвідношенням (1.50). При цьому значення шуканої функції в вузлах Y (xi) наближено замінюємо відповідними значеннями сіткової функції yi. Записуючи рівняння (1.54) в кожному вузлі з використанням зазначених аппроксимаций, отримуємо
Позначимо рi, fi відповідно величини. Після нескладних перетворень наведемо останню рівність до виду
Вийшла система n- 1 лінійних рівнянь, число яких збігається з числом невідомих значень сіткової функції в вузлах. Її значення на кінцях відрізка визначені граничними умовами (1.55):
Вирішивши систему рівнянь (1.56) з урахуванням умов (1.57), знайдемо значення сіткової функції, які наближено дорівнюють значенням шуканої функції. Покажемо, що таке рішення існує і сходиться до точного рішення при h → 0.
Для доказу існування рішення розглянемо систему лінійних рівнянь (1.56). Її матриця є трехдіагональной; на головній діагоналі знаходяться елементи. Оскільки р (х)> 0, то pi> 0, і діагональні елементи матриці переважають над іншими, так як в кожному рядку модулі цих елементів більше суми модулів двох інших елементів, кожен з яких дорівнює одиниці. При виконанні цієї умови рішення системи лінійних рівнянь існує і єдино.
Що стосується збіжності рішення, то тут має місце наступне твердження.
Затвердження. Якщо функції р (х) іf (x) двічі безперервно мають похідні, то пріh → 0 разностное рішення рівномірно сходиться до точного зі скоростьюO (h2).
Це - достатня умова збіжності методу скінченних різниць для крайової задачі (1.54), (1.55).
Система лінійних алгебраїчних рівнянь (1.56) з трехдіагональной матрицею може бути вирішена методом прогонки. При цьому умова р (х)> 0 гарантує виконання умови стійкості прогонки.
Цей метод на практиці використовується також і при р (х)<0, хотя успешный результат заранее предвидеть трудно. Для оценки получаемого решения в этом случае необходимо провести расчеты для разных значений шага (не менее трех) и убедиться в том, что полученные значения функции в одних и тех же узлах близки между собой и разность их уменьшается, что говорит о стремлении решения к некоторому пределу при h → 0.
Ми розглянули найпростіший випадок лінійного рівняння. Значно важче вирішувати нелінійні задачі. Розглянемо крайову задачу для рівняння другого порядку:
Використовуючи метод кінцевих різниць, отримуємо систему різницевих нелінійних рівнянь
В теорії різницевих схем доводиться, що різницеве рішення, яке визначається різницевими рівняннями (1.59), при h → 0 сходиться до точного. Достатня умова збіжності має вигляд
Система нелінійних алгебраїчних рівнянь (1.59) може бути вирішена ітераційними методами. Для її вирішення використовують також метод лінеаризації, тобто зведення рішення нелінійної системи до вирішення послідовності систем лінійних алгебраїчних рівнянь.
Нехай знайдено рішення системи (1.59) на k -ойітераціі. Тоді, підставляючи відомі значення в праві частини системи (1.59), отримуємо
Отже, ми прийшли до рішення системи лінійних алгебраїчних рівнянь щодо значень уi на (k + 1) -ої ітерації. Оскільки матриця цієї системи трехдіагональной, то для її вирішення на кожній ітерації може бути використаний метод прогонки. Потрібно лише поставити деякі початкові наближення; значення у0, уnпрі цьому визначені граничними умовами (1.60).
Слід зазначити, що збіжність даного ітераційного процесу досить повільна. Достатня умова збіжності має вигляд
Ця умова, а також умова (1.61) накладають обмеження на праву частину f (x, Y) вихідного рівняння (1.58).