Класифікація відбувається в умовах вільного або обмеженого падіння зерен. Вільне падіння являє собою рух одиничних зерен в середовищі, що виключає їх взаємний вплив один на одного. Під обмеженим падіння третьому розуміється рух безлічі зерен у вигляді такої маси, коли крім гравітаційних сил і сил опору сере-ди на рух зерен впливає динамічне віз-дію безперервно стикаються оточуючих зерен.
Швидкість вільного падіння зерна визначається соотно-ням сили тяжіння, підйомної (архимедовой) сили і сили з-спротиву середовища, яка залежить від режиму руху зерна.
При ламінарному режимі тіло рухається з малою скоро-стю, потоки середовища як би омивають його, не утворюючи завихрюючись-ний. Опір РВ визначається головним чином в'язко-стю середовища # 956; і кількісно описується законом Стокса:
де v - швидкість руху зерна; d - діаметр зерна.
Турбулентний режим руху характерний для високих швидкостей руху і супроводжується утворенням вихорів у поверхні тіла і позаду нього. Динамічне або інерції-онное опір середовища переміщенню тіла змінюється в цьому випадку за законом Ньютона - Ріттінгера:
де k - коефіцієнт (рівний 1/2, по Ріттінгеру); F - площа проекції тіла (дорівнює для кулі); - щільність середовища.
В реальних умовах рухається зерно відчуває од-ночасно дію як опору від в'язкості Рм. так і динамічного опору Рд. але ступінь їх прояву різна. Характеристикою співвідношення сил опорів Рд і Рв і, отже, режиму руху мінерального зер-на в середовищі є безрозмірний параметр Рейнол'дса (Rе)
звідки в загальному вигляді:
При значеннях Rе <1 наблюдается ламинарный режим движения частиц, размер которых не превышает 0,1 мм. При значениях Rе> 1000 і розмір часток більше 2 мм спостерігається турбулентний режим руху. Перехідний області від лами-Нарнії до турбулентного режиму руху відповідають зна-ня Rе від 1 до 1000, а крупність частинок від 0,1 до 2 мм. Опір середовища для цієї області можна розрахувати за формулою Аллена:
Якщо підставити значення ц з формули (3.7) в висловлю-ня (2.5) (2.9)
і порівняти вирази для Рд [формула (3.6)], для Ра [формула (2.8)] і для Рм [формула (2.9)], то виявимо, що загальний закон опору середовища руху зерна описується формулою
де # 936; = .f (Re) - коефіцієнт опору. Графічне з-браженіе залежності # 936; = .f (Re) в логарифмічних координацію-Натах, що носить назву діаграми Рейлея (рис. 2.5, крива # 936; ), Вказує на поступовий перехід від ламінарного до турбу-лентному режиму руху в міру зростання параметра Rе.
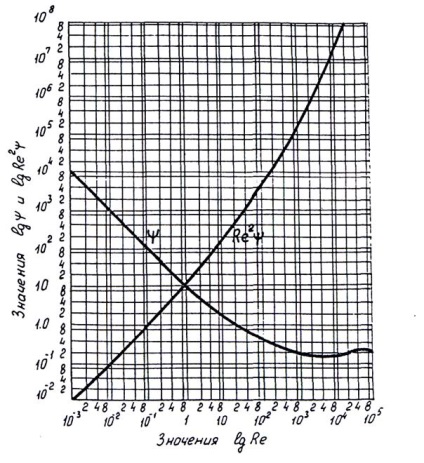
Мал. 2.5.Завісімость коефіцієнта опору # 936; і параметра Re 2 # 936; від числа Рейнольдса (Rе)
Гравітаційна сила G. викликає падіння зерна, бу-дет визначатися вагою тіла в середовищі. Відповідно до закону Архімеда для кулястого тіла об'ємом
де # 948; - щільність зерна; g - прискорення сили тяжіння.
Результуюча сила Р1 прискорює рух зерна в середовищі, визначиться як різниця між гравітаційної силою G і силою опору Р [формула (2.10)]
Збільшення швидкості руху частинок в початковий мо-мент під дією гравітаційної сили викликає возрас-тане опір середовища і через долі секунди частка починає падати з постійною швидкістю v0
У цих умовах і
звідки (для загального випадку):
При ламінарному режимі, на підставі рівнянь (2.5) і (2.11):
(Закон Стокса). (2.14)
При перехідному режимі, на підставі формул (2.8) і (2.11):
З урахуванням виразу для Rе:
(Закон Алена) (2.15)
При турбулентному режимі, на підставі формул (2.6) і (2.11):
(Закон Ріттінгера). (2.16)
Універсальний метод, придатний для визначення ко-кінцевих швидкостей руху зерен будь крупності, щільно-сті, форми, запропонував П.В. Лященко. Він врахував, що на основа-нии формул (2.7) і (2.10) можна скласти систему рівнянь:
в результаті спільного рішення якої отримаємо висловлю-ня для параметра Rе 2 # 936;
Оскільки при сталому русі Р = G, то, під-ставлю в формулу (2.18) замість Р вираз для G з фор-мули (2.11), знаходимо:
За рівняння (2.19) на підставі відомих параметрів зерна і середовища легко розрахувати значення параметра Rе 2 # 936; і ис-користувати його для визначення параметра Rе по діаграмі Rе 2 # 936; = F (Rе), побудованої на основі діаграми Рейлея # 936; = F (Re) і зображеної на рис. 2.5. Після цього можна визна-ділити кінцеву швидкість падіння частки або непосредст-кої підстановкою отриманого значення Rе в формулу (2.7) або підстановкою значення # 936 ;, знайденого за значенням Rе на діаграмі Рейлея (див. Рис. 2.5, крива # 936;), в формулу (2.13).
Приклад 1.Определить кінцеву швидкість руху в воді зерна вугілля розміром d = 25 мм (0,025 м), щільністю # 948; = 1350 кг / м 3. приймаючи дина-мічного коефіцієнт в'язкості води при температурі 293 К рівним # 956; = 0,001 Н-с / м 2. щільність # 916; = 1000 кг / м 3 g = 9,81 м / с 2.
За формулою (3.19) значення Rе 2 # 936; дорівнює 2807 × 10 4. На діаграмі Rе 2 # 936; = F (Rе) (див. Рис. 3.5) цього значення відповідає значення Rе = 12400. За формулою (3.7) v = v0 = 0,496 м / с. Розрахунок швидкості за формулою (3.13) для значення # 936; = 0,183 (відповідного знайденому значенню Rе = 12400) показує ідентичні результати.
Приклад 2. Визначити кінцеву швидкість руху в повітрі зерна кварцу розміром d = 1 мм (0,001 м), щільністю # 948; = 2500 кг / м 3. приймаючи динамічний коефіцієнт в'язкості повітря # 956; = 0,00002 Н-с / м 2. пліт-ність # 916; = 1,23 кг / м 3.
За формулою (3.19) значення Rе 2 # 936; = 39 447. На діаграмі (див. Рис. 3.5) цього значення відповідає Rе = 400. За формулою (3.7) швидкість v = v0 = 7, 18 м / с.
При розрахунку швидкостей падіння зерен неправильної фор-ми користуються еквівалентним діаметром d е частинок, т. Е. Діаметром кулі, однакового з часткою обсягу:
і в розрахункові формули вводять поправочний коефіцієнт форми Кф, що є відношенням поверхні одно-великого кулі до поверхні зерна неправильної форми і рав-ний: 1,0 - при кулястої; 0,8-0,9 - прі округлої; 0,7 - 0,8 - при незграбною; 0,6 - 0,7 - при пластинчастої формі частинок.
Швидкість туги падіння V ст зерен завжди менше ско-рости їх вільного падіння Vо (наприклад, для кварцу в 2,76 рази, для галеніту в 3,47 рази). Встановлено істотна за-лежність швидкості туги падіння від ступеня розпушення або виваженості мінеральних часток в середовищі, харак-терізуемой коефіцієнтом розпушення # 920; Р. рівним відно-шенням обсягу вільного простору між зернами до пів-ному об'єму, що займають розпушеному сумішшю (значення завжди менше 1). За П. В. Лященко,
Формула (2.20) придатна для визначення швидкості Стесі-ненного падіння зерен розміром менше 0,2 мм при класси-фікації тонкозернистого матеріалу. Для визначення вуст бо-леї великих зерен - від 0,2 до 12,5 мм - користуються фор-мулою Ханкока:
Зерна різної крупності і щільності, але мають оди-кові кінцеві швидкості руху в середовищі, називаються равнопадающімі, т. Е. V01 = v02. У загальному випадку на підставі формули 2.13:
Ставлення діаметрів равнопадающіх легкого і важко-го зерен називається коефіцієнтом рівнопадіння (е).
Позначивши через К1 і К2 постійні коефіцієнти, вчи-тивающие вплив реологічних параметрів середовища і форми відповідно для легких і важких зерен на підставі фор-мул (2.14) - (2.16) знаходимо:
для ламінарного режиму руху [формула (2.14)]
для перехідного режиму руху [формула (2.15)]
для турбулентного режиму руху [формула (2.16]
У матеріалі, що надходить на гравітаційне збагачені-ня, засноване на використанні відмінності швидкостей паде-ня поділюваних зерен, не повинні бути присутніми їх равнопадающіе зерна. Для цього матеріал піддають попередньо-котельної класифікації по крупності, шкала (модуль) кото-рій не повинна перевищувати коефіцієнт рівнопадіння.