1 РОЗРОБЛЕНО І ВНЕСЕНО Технічним комітетом зі стандартизації ТК 125 «Статистичні методи в управлінні якістю продукції»;
АТ «Науково-дослідний центр контролю і діагностики технічних систем» (АТ «НДЦ КД»)
3. Цей Стандарт, за винятком додатка В, являє собою автентичний текст міжнародного стандарту ІСО 7966-93 «Приймальні контрольні карти»
4 ВВЕДЕНО ВПЕРШЕ
1 Область застосування. 2
2 Нормативні посилання. 2
3 Визначення. 3
4 Позначення і скорочення. 3
5 Опис практики застосування приймальних контрольних карт. 4
6 Приймальний контроль процесів. 5
7 Встановлення параметрів процесу. 6
8 Процедури обчислень. 7
10 Коефіцієнти для приймальних контрольних меж. 16
Додаток А Номограми для побудови приймальних контрольних карт. 18
Додаток В Статистичний приймальний контроль якості продукції з урахуванням вимог ГОСТ Р 50779.30 при застосуванні постачальником приймальних контрольних карт. 26
Приймальна контрольна карта з'єднує розгляд питань управління процесом з елементами приймального вибіркового контролю. Вона є засобом, що допомагає прийняти рішення щодо прийнятності процесів. Основи для прийняття рішень можуть виражатися в постановці таких питань:
b) чи має рівень процесу зрушення з деякою допустимої зони.
На відміну від більшості підходів приймального вибіркового контролю акцент робиться на прийнятність процесу, а не продукції.
На відміну від традиційних підходів, заснованих на контрольних картах, в цьому випадку процесу необов'язково бути поблизу деякого єдиного стандартного рівня процесу до тих пір, поки мінливість всередині підгруп залишається задовільною. Він може (для мети приймання) протікати на будь-якому рівні або рівнях в деякій зоні рівнів процесу, які є прийнятними з точки зору вимог технічних допусків. Таким чином, припускають, що деякі особливі причини створюють досить малі зрушення рівня процесу щодо встановлених вимог і неекономічно коригувати рівень процесу тільки для мети приймання.
Хоча застосування приймальної контрольної карти все ж сприяє виявленню та усуненню особливих причин для цілей безперервного вдосконалення процесу.
Необхідна перевірка на притаманну процесу стабільність. Для цього спостереження ведеться з застосуванням контрольних карт Шухарта (карт розмахів або стандартних відхилень вибірки) для підтвердження того, що мінливість, властива раціональним підгрупах, залишається в стійкому стані. Додатковим джерелом інформації для управління процесом є дослідження розподілу розглянутих рівнів процесу. Для перевірки правомірності застосування приймальної контрольної карти слід проводити попереднє вивчення процесу за допомогою контрольної карти Шухарта.
ДЕРЖАВНИЙ СТАНДАРТ УКРАЇНИ
В - фактор з граф 3 або 7.
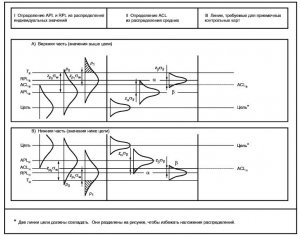
Малюнок 2 - Межі та визначальні елементи приймальних контрольних карт
Для обсягу вибірок, рівного чотирьом одиницям і більше, справедливо припущення про нормальність розподілу для. Однак інтерпретація часток (відсотків) невідповідних одиниць, пов'язаних з APL і RPL, залежить від вихідного розподілу. Наприклад, для інших розподілів ймовірності слід користуватися відповідними таблицями і замінити значення квантилів стандартного нормального закону розподілу на необхідні значення. (В деяких джерелах замість zр? Застосовують символи U або t?). Вибір z підкреслює, що запропонований відстань - це абсолютна різниця між центром розподілу і областю хвоста, в той час як U представляє різницю між мінус. і областю хвоста. Перевага застосування z в тому, що кордони і визначальні елементи потрапляють вище і нижче центру, так що зручно мати однакові значення a і b з двох сторін від мети. Це допомагає і в геометричній інтерпретації розташування ліній на карті (див. Малюнок 1):
де Тв. Тн- верхня і нижня межі поля допуску;
zрo - квантиль стандартного нормального закону розподілу рівня р0 (для прийнятною частки або відсотка невідповідних одиниць продукції);
sw - стандартне відхилення всередині підгрупи.
У прикладі 1 розділу 9 визначені з APL і RPL через відсотки невідповідних одиниць продукції.
У деяких випадках вибір значення APL може бути безпосередньо не пов'язаний з межами поля допуску і його можна вибрати довільно. Досвід показує, що «неекономічні» або «труднорегуліруємий» причини зрушень рівня процесу відповідають досить вузькій зоні. Кордон цієї зони може бути довільно позначена як APL (приклад 2 в розділі 9). В цьому випадку не потрібні припущення про нормальність розподілу.
Подібним чином можна вибрати RPL декількома способами. Він може бути пов'язаний з межами поля допуску за допомогою визначається неприйнятною частки (відсотком) невідповідних одиниць продукції р1. яка може виникнути в тому випадку, коли процес центрирован на RPL.
де Тв. Тн- верхня і нижня межі поля допуску;
zp1- квантиль стандартного нормального закону розподілу рівня р1 (для частки або відсотка невідповідних одиниць продукції);
sw - стандартне відхилення всередині раціональної підгрупи.
У деяких випадках вибір RPL може бути довільним, якщо є відчуття, що рівень процесу не перевищить деяку відстань від цільового значення.
Оскільки APL і. RPL і b обрані, то верхню приймальну кордон ACLв розраховують за формулою
де za і zb - квантилі стандартного нормального закону розподілу рівня. і b відповідно.
Нижню межу ACLн розраховують за формулою
Якщо ризики a і b обрані рівними, приймальна контрольна межа лежить посередині між APL і RPL.
Обсяг вибірки можна обчислити за формулою
Для асиметричних кордонів (розділ 7) обсяг вибірки обчислюють за формулою
Замість цих обчислень можна застосувати номограмму або криву оперативної характеристики (ОХ). Приклади застосування формул і номограм наведені в додатку А.
8.1.2 Визначення елементів APL. b і n
APL вибирають, як зазначено в 8.1.1. Обсяг вибірки можна взяти, виходячи з практичних міркувань і зручності в роботі, або встановити його як пробне значення для оцінки значень RPL і b. Якщо обсяг вибірки незадовільний, процес можна повторити або обчислити п за допомогою представлених комбінацій, причому значення APL, a і n повинні бути задані:
Див. Приклад застосування 2 в розділі 9.
8.1.3 Визначення елементів RPL, a, b і n
RPL вибирають, як зазначено в 8.1.1. Як і при співвідношеннях в 8.1.2, обсяг вибірки може бути встановлений з практичних міркувань або виведений методом ітерації, причому значення RPL, b і n повинні бути задані:
Див. Приклад застосування 3 в розділі 9.
8.1.4 Визначення елементів ACL, a, b і n
ACL і n можна вибрати на основі системи управління Шухарта і далі обчислити значення APL з ризиком a і RPL з ризиком b, причому значення ACL і n повинні бути задані:
Див. Приклад застосування 4 в розділі 9.
8.2Частота взяття вибірок
Співвідношення між обсягом вибірки і ризиками a і b було розглянуто вище. Частота взяття вибірок в цьому стандарті не розглядається. Якщо процес стабільний на досить тривалому проміжку часу з точки зору мінливості, і зрушення рівня спостерігалися в межах зони прийнятних процесів, частота вибірок може бути відносно низькою в порівнянні з менш стабільними процесами. Втрати від помилкових рішень повинні в деякій мірі враховуватися при виборі значень a і b, хоча вони також тісно пов'язані з частотою взяття вибірок.
8.3Другіе випадки
У разі контролю частки (відсотка) невідповідних одиниць продукції р або числа невідповідностей з хід міркувань той же. Для р-карт APL визначають як р0. a RPL - як р1. Для з-карт значення С0 і з1 зазвичай не пов'язані з числом одиниць продукції, що виходять за межі.
Для виявлення зрушень рівня процесу або числа одиниць продукції, що виходять за межі, слід застосовувати р- і з-карти Шухарта. Це призводить до двосторонніх кордонів для отримання інформації про поліпшення або погіршення роботи процесу. Приймальні контрольні карти (р- і з-карти) більш тісно пов'язані з планами приймального вибіркового контролю, але висновки робляться щодо процесу, а не партії одиниць продукції. Приймальна контрольна карта розглядає b-ризик прийняття підвищених рівнів невідповідності і a-ризик відхилення процесів, зосереджених на р0, при цьому можуть бути визначені відповідні обсяг вибірки і приймальні контрольні кордону.
Вихідним розподілом для р-карти є біноміальний розподіл, а для з-карти - пуассоновским. Більшість контрольних карт Шухарта для ознак придатне для цілей управління і використовує апроксимації нормального розподілу (тобто), якщо р не дуже мало [де - вибіркове стандартне відхилення для середньої частки невідповідних одиниць продукції в підгрупах, що розраховується за формулою; - вибіркове стандартне відхилення для середнього числа невідповідностей в підгрупах, що розраховується за формулою (див. ГОСТ Р 50779.40)].
Якщо потрібна гранична точність (1 до 1000), то може бути краще застосовувати імовірнісні межі.
9.1Прімер 1 (малюнки А.3 і А.4 додатка А)
Операція: наповнення розчином пляшок місткістю (10,0 ± 0,5) см 3.
Вимірювання: обсяг розчину (при номінальному значенні 10 см 3).
Мінливість: Відомо, що притаманна мінливість через випадкових причин має нормальний розподіл. З минулого досвіду встановлено s = 0,1 см 3.
Мета: процес приймається, якщо наповнення менш 0,1% кількості пляшок виходить за межі (10,0 ± 0,5) см 3.
Процес відхиляється, якщо більше 2,5% кількості пляшок виходить за ці межі.
Для обчислення APL і RPL використовують такі дані:
Критичне значення z нормального розподілу (відтинає площа хвоста, рівну встановленої частці перевищення обсягом пляшок кордонів поля допуску):