Коло завдань, що вирішуються вищої геодезією, прийнято поділяти на наукові та науково - технічні.
Головною наукової завданням вищої геодезії є вивчення фігури (форми і розмірів) і гравітаційного поля Землі за даними геодезичних, гравіметричних вимірювань, астрономічних визначень і спостережень штучних супутників Землі.
Вирішення цього завдання включає в себе два основних пункти:
а) Визначення виду і розмірів математично простий поверхні (поверхні належності), досить добре представляє фігуру Землі в цілому.
б) Вивчення дійсної фігури Землі, тобто реальної фізичної земної поверхні, і її зовнішнього гравітаційного поля.
Як поверхні належності приймають поверхню еліпсоїда обертання з малим полярним стисненням, який називається земним еліпсоїдом. Визначення поверхні земного еліпсоїда полягає у встановленні параметрів, що характеризують його розміри, форму і розташування (орієнтування) в тілі Землі.
Вивчення дійсної фігури Землі полягає у визначенні геометричних величин, що характеризують відступу її поверхні від поверхні встановленого земного еліпсоїда.
Зовнішнє гравітаційне поле Землі вивчають за таким же принципом, що і фігуру Землі: спочатку визначають гравітаційне поле земного еліпсоїда (нормальної Землі), а потім визначають відступ гравітаційного поля реальної Землі від гравітаційного поля обраного еліпсоїда.
До числа інших наукових завдань вищої геодезії відносяться, перш за все, геодинамічні дослідження, тобто вивчення сучасних рухів земної кори (СДЗК), рухів земних полюсів, визначення різниць рівнів і переміщень берегових ліній морів і океанів.
Науково-технічні завдання вищої геодезії полягають:
1. У створенні опорних мереж: геодезичної, що забезпечує планові і висотні координати, і гравіметричної, що дає абсолютні значення прискорення сили тяжіння.
2. У розробці та вдосконаленні методів високоточних вимірювань (лінійних, кутових, нівелювання, астрономічних визначень, спостережень ШСЗ, гравіметричних).
3. У розробці методів математичної обробки результатів зазначених в пункті 2 вимірювань і у виконанні цієї обробки.
Зауважимо, що методами вищої геодезії визначаються координати окремих, дискретних точок земної поверхні, тобто пунктів державних опорних мереж. Надалі координати цих пунктів використовуються як вихідні для детального вивчення між ними форми фізичної поверхні Землі методами топографії. Топографія, використовуючи опорну геодезичну мережу, вже не вимагає застосування теорії вищої геодезії.
Крім того, важливо відзначити, що методи і прилади, що розробляються у вищій геодезії, знаходять все зростаюче застосування в практиці будівництва різних інженерних споруд - наукових, промислових, гідро і теплоенергетичних, транспортних і т.д.
1.2. Поняття про геоїде, квазігеоїда, земному еліпсоїді
Геоид, квазігеоїда і загальний земний еліпсоїд - це три моделі Землі. Дамо їх визначення з точки зору сучасних уявлень про фігуру Землі.
Під фігурою Землі в даний час розуміють фігуру, обмежену фізичної поверхнею Землі, тобто поверхнею її твердої оболонки на суші і невозмущенной поверхнею морів і океанів.
Суша становить третю частину від земної поверхні і в середньому вона підноситься над водою приблизно на 900 метрів, що мало в порівнянні з радіусом Землі (6371км). Тому за фігуру Землі в першому наближенні прийнятий геоид.
Дамо два визначення геоид:
Суворе: геоид - це рівень поверхні поля сили тяжіння Землі, що проходить через початок рахунку висот.
Схожі: геоид - етофігура, обмежена невозмущенной поверхнею морів і океанів і продовжена під материками так, щоб стрімкі лінії у всіх її точках були перпендикулярні до неї.
Понад сто років, т. Е. З першої половини минулого століття геодезисти і геофізики вивчали фігуру геоїда і вважали це основний наукової завданням вищої геодезії. В середині минулого століття радянським вченим Молоденським було доведено, що фігура геоїда, строго кажучи, невизначена. Він запропонував основним завданням вищої геодезії вважати вивчення фігури реальної Землі і її гравітаційного поля. Молоденський створив теорію, яка дозволяє точне визначення фігури Землі на підставі виконаних на земній поверхні вимірів, без залучення будь - яких гіпотез про її внутрішню будову.
В теорії Молоденського в якості допоміжної вводиться поверхню квазігеоїда, що збігається з геоидом на океанах і морях і вельми мало відступаюча від поверхні геоїда на суші (менше 2м).
На відміну від геоїда поверхню квазігеоїда може бути строго визначена за результатами наземних спостережень.
З поняттям земного еліпсоїда ми вже зіткнулися при розгляді головної наукової задачі вищої геодезії. Нагадаю, що поверхня земного еліпсоїда є тією математично і геометрично простою поверхнею, на якій можуть бути вирішені геодезичні завдання з координування точок земної поверхні і яка достатньою близька до поверхні Землі. Земний еліпсоїд є еліпсоїд обертання з малим полярним стисненням. Його поверхня може бути отримана обертанням напівеліпса РЕР1 навколо його малої осі РР1 (рис 1.2).
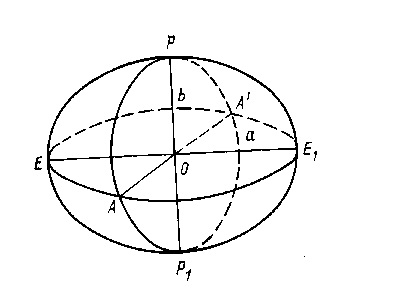
Мал. 1.2. До поняття земного еліпсоїда:

Поверхня земного еліпсоїда в геодезії приймають за відліковий, визначаючи щодо неї висоти точок поверхні досліджуваної фігури Землі.
Форма і розміри земного еліпсоїда характеризуються великою і малою півосями



або велика піввісь

Еліпсоїд, що має найбільшу близькість до фігури Землі в цілому, називається загальним земним еліпсоїдом.
Параметри загального земного еліпсоїда визначаються під умовами:
центр еліпсоїда повинен збігатися з центром мас Землі, а його мала вісь з віссю обертання Землі 1;
обсяг еліпсоїда повинен бути дорівнює обсягу геоїда (квазігеоїда);
Сума квадратів відхилень по висоті поверхні еліпсоїда від поверхні геоїда (квазігеоїда) повинна бути мінімальною.
Параметри земного еліпсоїда можуть бути отримані за допомогою так званих градусних вимірювань. полягають в прокладанні рядів тріангуляції за напрямками меридіанів і паралелей на різних широтах з визначенням на кінцевих пунктах астрономічних широт, довгот і азимутів сторін, а також за результатами супутникових спостережень.
Протягом півтора століття вчені різних країн займалися визначенням параметрів земного еліпсоїда, використовуючи доступні їм результати градусних вимірювань. Підсумком цих визначень є поява низки еліпсоїдів, найбільш відомі з яких представлені в таблиці 1.1.
Параметри найбільш відомих земних еліпсоїдів