Тепер згадаємо проблему індички. Ви озираєтеся назад і, спираючись на минулий досвід, виводите якісь правила для майбутнього. Так ось, прогнози на підставі минулого досвіду чреваті і більш серйозними каверзами, ніж розібрані нами вище. Справа в тому, що одні й ті ж дані можуть служити підставою для кардинально протилежних теорій! Якщо ви доживете до завтра, це може означати, що: а) у вас виростуть шанси досягти безсмертя; б) ви ще трохи наблизитися до смерті. Обидва висновки повинні базуватися на одних і тих же даних. Якщо ви індичка, яку регулярно годують протягом довгого часу, ви можете або наївно припускати, що годування підтверджує вашу безпеку; або проявити проникливість і вирішити, що воно підтверджує небезпеку стати чиїмось святковою вечерею. Догідливість мого знайомого, проявлена в минулому, може означати щиру прихильність до мене і занепокоєння про моє благополуччя або - його користь і таємне бажання в один прекрасний день заволодіти моїм бізнесом.
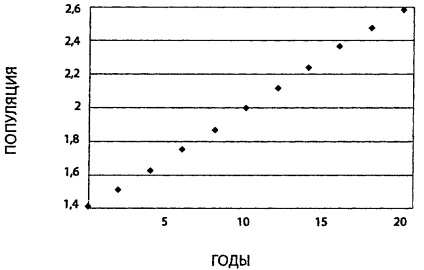
Ряд, що відображає видимий зростання популяції бактерій (або показників продажів, або будь-якої змінної, простежується в часі, на кшталт загальної кількості корму, з'їденого індичкою з глави 4).
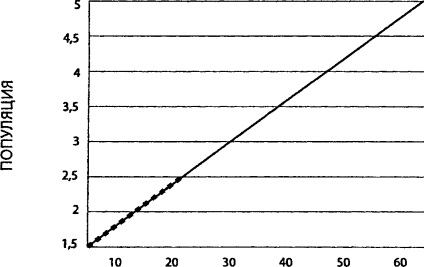
Легко вписується в тренд (тобто тенденцію): є одна, і тільки одна, лінійна модель, яка підходить до цих даних. Можна продовжувати її в майбутнє.
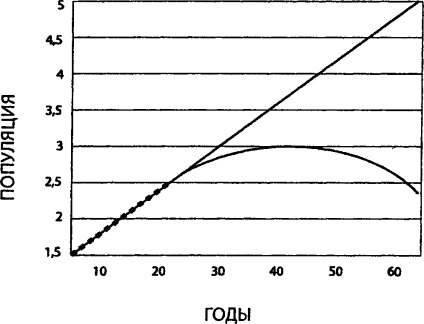
Дивіться в ширшому масштабі. Інші моделі теж підходять.
Реальний "генерує процес" гранично простий, але не має нічого спільного з лінійної моделлю! Лише деякі частини кривої здаються лінійними, і ми потрапляємо в пастку, екстраполюючи їх у вигляді прямої *.
Ці графіки ілюструють статистичний варіант наративної помилки - ви знаходите модель, в яку вкладається минуле. «Лінійна регресія» і «R-квадрат» здатні вкрай задурити вам голову. Можна дивитися на лінійну частину кривої і хвалитися високим R-квадратом, нібито свідчить про те, що в свій телевізор добре вкладаються дані і вона має велику прогностичної сили. Все це нісенітниця: вона годиться тільки для лінійного сегмента. Завжди пам'ятайте, що R-квадрат непридатний для Крайнестана. (R-квадрат - число від 0 до 1, яке відображає близькість значень лінії тренда до фактичних даних. Лінія тренда найбільш відповідає дійсності, коли значення R2 близько до 1. прим. Ред.)
Минуле може збивати з пантелику, більш того, в наших інтерпретаціях минулих подій є багато ступенів свободи.
Ось графічна ілюстрація цієї ідеї: подивіться на ряд точок, що представляє зміна якогось числа в часі (рисунок з), - графік схожий на малюнок 1 з глави 4, на якому відображена перша тисяча днів індички. Припустимо, вчитель просить вас продовжити ряд точок. З лінійної моделлю, тобто з лінійкою, ви намалюєте лише пряму лінію, одну пряму лінію від минулого до майбутнього (рисунок 4). Лінійна модель унікальна. Є одна, і тільки одна, лінія, яку можна побудувати на даній множині точок. Але все може виявитися набагато складніше. Якщо ви не будете зациклюватися на цій прямій, то виявите, що є величезна кількість кривих, самих різних конфігурацій, якими можуть зв'язуватися точки. Роблячи лінійний прогноз на підставі минулого, ви продовжуєте помічену тенденцію. Але кількість майбутніх можливих відхилень від цього курсу, заданого в минулому, нескінченно.
Філософ Нельсон Гудмен називає це проблемою індукції: ми будуємо пряму лінію лише тому, що у нас в головах лінійна модель, - той факт, щоб 1000 днів поспіль змінна збільшувалася, додає впевненості, що вона буде рости і далі. Але якщо у вас в голові є нелінійна модель, вона може показати, що на 1001-й день настане перелом.
Проблема індукції - це один з варіантів спотворення наративу; є нескінченно багато «історій», які пояснюють те, що ви бачили. Проблема, треба сказати, вельми серйозна: адже якщо не існує єдиного способу «узагальнити» відоме, щоб зробити припущення про невідомому, як же тоді діяти? Відповідь, зрозуміло, буде такий: треба покладатися на «здоровий глузд». Однак вашому здоровому глузду, можливо, буде дуже важко впоратися з деякими змінними на території Крайнестана.
Поділіться на сторінці