Завдання, подібні наведеної, демонструють використання процедури Пошуку рішення для підбору таких значень параметрів, які максимізують значення нелінійної функції.
Перш ніж знайомитися з прикладом цього листа, розглянемо спрощений варіант цього завдання: пошук максимуму функції при зміні одного параметра.
Вихідні дані завдання складаються з 2-х блоків: "Плановані показники" та "Дані про продукцію". Так, в 1-му кварталі заплановані наступні показники реалізації:
Дані про продукцію:
- ціна реалізації (комірка В17) - 40 грн;
- собівартість (осередок В18) - 25 грн.
Розрахунок планованих показників виробляють так:
- дохід з обороту визначається як очікувана кількість проданих одиниць продукції (осередок В4), помножене на собівартість продукції, тому в комірку В5 введемо формулу
- фраза "собівартість реалізованої продукції" на мові математики виглядає як
- накладні витрати фірми будемо обчислювати в обсязі 15% доходу з обороту, тобто в осередок B11 введемо формулу
- прибуток від продукції визначимо як валовий прибуток мінус валові витрати, тобто
Якщо перераховані вище дані і формули ввести в таблицю, то результати обчислень будуть такими, як показано на рис. 5.
Активізуємо Сервіс => Пошук рішення і опишемо умови вирішення задачі:
- задайте осередок B14, як що містить цільову функцію 4);
- визначте мету оптимізації - Максимальне значення;
- вкажіть клітинку, значення якої буде змінюватися при пошуку найкращого рішення 5) - B10;
- при призначенні параметрів вкажіть на нелінійність моделі. Для інших параметрів використовуйте установки за замовчуванням, які підходять для вирішення більшості завдань.
Клацнувши на кнопці Виконати. Ви побачите наступний результат оптимізації (рис. 6).
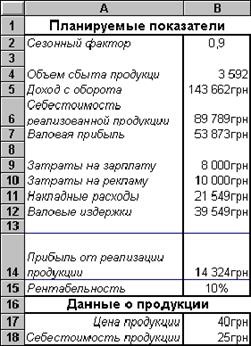
Малюнок 5 - Дані для пошуку екстремуму в задачі маркетингу
Покажіть, що функція
f = (x-1) 2 + y2 - 0,5cos (2z)
має мінімальне значення -0,5 при x = 1; y = -7,9E-07 і z = 3,14159.
В якості вихідних даних для пошуку мінімуму прийміть x = 1, y = 2 і z = 3.
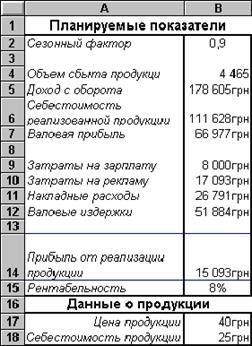
Малюнок 6 - Результат оптимізації