
1. Брокколі Романеско
Можливо побачивши брокколі Романеско в магазині, ви подумали, що це ще один зразок генномодифікованого продукту. Але насправді це ще один приклад фрактальної симетрії природи. Кожне суцвіття брокколі має малюнок логарифмічною спіралі. Романеско зовні схожа на брокколі, а за смаком і консистенції - на кольорову капусту. Вона багата на каротиноїди, а також вітамінами С і К, що робить її не тільки красивою, але і здоровою їжею.

Протягом тисяч років люди дивувалися ідеальної гексагональної формі сот і питали себе, як бджоли можуть інстинктивно створити форму, яку люди можуть відтворити тільки за допомогою циркуля і лінійки. Як і чому бджоли мають палке бажання створювати шестикутники? Математики вважають, що це ідеальна форма, яка дозволяє їм зберігати максимально можливу кількість меду, використовуючи мінімальну кількість воску. У будь-якому випадку, все це продукт природи, і це чертовски вражає.

Соняшники можуть похвалитися радіальної симетрією і цікавим типом симетрії, відомої як послідовність Фібоначчі. Послідовність Фібоначчі: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 і т.д. (Кожне число визначається сумою двох попередніх чисел). Якби ми не поспішали і підрахували кількість насіння в соняшнику, то ми б виявили, що кількість спіралей зростає за принципами послідовності Фібоначчі. У природі є дуже багато рослин (в тому числі і брокколі Романеско), пелюстки, насіння і листя яких відповідають цій послідовності, тому так важко знайти конюшина з чотирма листочками.
Але чому соняшник та інші рослини дотримуються математичні правила? Як і шестикутники в вулику, все це - питання ефективності.

4. Раковина Наутілуса
Крім рослин, деякі тварини, наприклад Наутілус, відповідають послідовності Фібоначчі. Раковина Наутілуса закручується в «спіраль Фібоначчі». Раковина намагається підтримувати одну і ту ж саму пропорційну форму, що дозволяє їй зберігати її протягом усього життя (на відміну від людей, які змінюють пропорції протягом життя). Не всі Наутилуси мають раковину, вибудувану за правилами Фібоначчі, але всі вони відповідають логарифмічною спіралі.
Перш, ніж ви позавідуете молюскам-математикам, згадайте, що вони не роблять цього спеціально, просто така форма найбільш раціональна для них.

Більшість тварин мають двосторонню симетрію, що означає, що вони можуть бути розділені на дві однакових половинки. Навіть люди мають двосторонньою симетрією, і деякі вчені вважають, що симетрія людини є найбільш важливим фактором, який впливає на сприйняття нашої краси. Іншими словами, якщо у вас однобоке особа, то залишається сподіватися, що це компенсується іншими хорошими якостями.
Доходить навіть до повної симетрії в прагненні залучити партнера, наприклад павич. Дарвін був позитивно роздратований цим птахом, і написав в листі, що «Вид пір'я в хвості павича, всякий раз, коли я дивлюся на нього, робить мене хворим!» Дарвіну, хвіст здавався обтяжливим і не мають еволюційного сенсу, так як він не відповідав його теорії «виживання найбільш пристосованих». Він був в люті, поки не придумав теорію статевого відбору, яка стверджує, що тварини розвивають певні функції, щоб збільшити свої шанси на спаровування. Тому павичі мають різні пристосування для залучення партнерки.

Є близько 5000 типів павуків, і всі вони створюють майже ідеальне круговий полотно з радіальними підтримують нитками майже на рівній відстані і спіральної тканиною для лову видобутку. Вчені не впевнені, чому павуки так люблять геометрію, так як випробування показали, що кругле полотно не заманить їжу краще, ніж полотно неправильної форми. Вчені припускають, що радіальна симетрія рівномірно розподіляє силу удару, коли жертва потрапляє в мережі, в результаті чого виходить менше розривів.

Дайте парі ошуканців дошку, косарки і рятівну темряву, і ви побачите, що люди теж створюють симетричні форми. Через те, що кола на полях відрізняються складністю дизайну і неймовірною симетрією, навіть після того, як творці кіл зізналися і продемонстрували свою майстерність, багато людей до сих пір вірять, що це зробили космічні прибульці.
В міру ускладнення кіл все більше прояснюється їх штучне походження. Нелогічно припускати, що прибульці робитимуть свої повідомлення все більш важкими, коли ми не змогли розшифрувати навіть перші з них.
Незалежно від того, як вони з'явилися, кола на полях приємно розглядати, головним чином тому, що їх геометрія вражає.
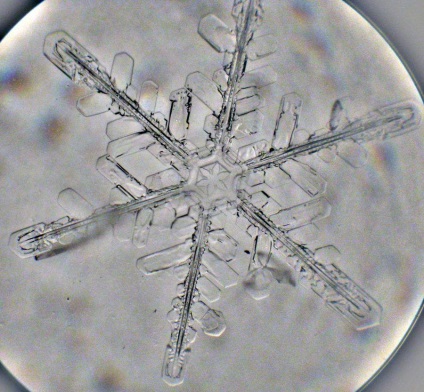
Навіть такі крихітні освіти, як сніжинки, регулюються законами симетрії, так як більшість сніжинок має шестигранну симетрію. Це відбувається зокрема через те, як молекули води вишиковуються, коли тверднуть (кристалізуються). Молекули води набувають твердий стан, утворюючи слабкі водневі зв'язки, вони вирівнюються в упорядкованому розташуванні, яке врівноважує сили тяжіння і відштовхування, формуючи гексагональную форму сніжинки. Але при цьому кожна сніжинка симетрична, але жодна сніжинка не схожа на іншу. Це відбувається тому, що падаючи з неба, кожна сніжинка відчуває унікальні атмосферні умови, які змушують її кристали розташовуватися певним чином.

9. Галактика Чумацький Шлях
Як ми вже бачили, симетрія і математичні моделі існують майже всюди, але хіба ці закони природи обмежуються нашою планетою? Очевидно, немає. Нещодавно відкрили нову секцію на краю Галактики Чумацького Шляху, і астрономи вважають, що галактика являє собою майже ідеальне дзеркальне відображення себе.

10. Симетрія Сонця-Місяця
Якщо врахувати, що Сонце має діаметр 1,4 млн. Км, а Місяць - 3474 км, здається майже неможливим те, що Місяць може блокувати сонячне світло і забезпечувати нам близько п'яти сонячних затемнень кожні два роки. Як це виходить? Так співпало, що поряд з тим, що ширина Сонця приблизно в 400 разів більше, ніж Місяць, Сонце також в 400 раз далі. Симетрія забезпечує те, що Сонце і Місяць виходять одного розміру, якщо дивитися з Землі, і тому Місяць може закрити Сонце. Звичайно, відстань від Землі до Сонця може збільшуватися, тому іноді ми бачимо кільцеві і неповні затемнення. Але кожні один-два роки відбувається точне вирівнювання, і ми стаємо свідками захоплюючих подій, відомих як повне сонячне затемнення. Астрономи не знають, як часто зустрічається така симетрія серед інших планет, але вони думають, що це досить рідкісне явище. Тим не менш, ми не повинні припускати, що ми особливі, так як все це справа випадку. Наприклад, щороку Місяць віддаляється приблизно на 4 см від Землі, це означає, що мільярди років тому кожне сонячне затемнення було б повним затемненням. Якщо і далі все піде так, то повні затемнення, в кінці кінців, зникнуть, і це буде супроводжуватися зникненням кільцевих затемнень. Виходить, що ми просто перебуваємо в потрібному місці в потрібний час, щоб побачити це явище.