1. Поняття абсолютної стійкості
2. Критерій абсолютної стійкості Попова
3. Дослідження абсолютної стійкості при нестійкій лінійної частини
4. Круговий критерій Воронова
5. робастний стійкість
1. Поняття абсолютної стійкості
Метод абсолютної стійкості застосовується для дослідження стійкості нелінійних систем, коли значення характеристик нелінійних елементів відомі неточно. Неповнота інформації може бути пов'язана з похибкою изго? Лення, зі зневагою деякими чинниками, зі старінням елементів і т.п. Для того щоб гарантувати стійкість сис? Тим, незважаючи на неповну інформацію про нелінійний, було введено поняття абсолютної стійкості. З цією ж метою вводяться класи нелинейностей [4]. Для прикладу, на рис 1 показані нелінійності з класу. За визначенням до цього класу належать усі нелінійні функції, графік яких розташовується між прямими і. де.
Найчастіше використовуються такі різновиди класів нелінійностей даного типу: [0; k], (рис. 1, б); клас (рис. 2, а); клас [k 1; k 2] причому. (Рис. 2, б). Існують і інші класи нелинейностей, що визначаються більш складними виразами [2, 4].
Практично, клас тієї чи іншої нелінійності повинен бути обраний таким чином, щоб в процесі старіння, зносу елементів системи або при будь-яких інших природних змінах нелінійність зберігала свою приналежність до початкового класу.
Визначення. Система називається абсолютно вус? Тойчивость. якщо її єдине положення рівноваги асимптотично стійко в цілому за будь-якої нелі? нейності із заданого класу.
2. Критерій абсолютної стійкості Попова
Для дослідження абсолютної стійкості запропонований ряд критеріїв абсолютної стійкості. Найбільшого поширення з них отримали наступні два: критерій стійкості В. М. Попова та кругової критерій, запропонований А. А. Вороновим.
Критерій Попова використовується для дослідження абсолютної стійкості систем з нелінійністю з класу [0, k], де. Для застосування цього критерію структурна схема системи приводиться до виду, показаному на рис. 3.
де # 150; управління, # 150; вектор станів.
Перейшовши в (1) і (3) до зображень по Лапласа, отримаємо
Критерій В. М. Попова може застосовуватися лише в тих випадках, коли виконуються наступні умови:
в) Лінійна система, отримана з нелінійної при заміні на. стійка асимптотично, тобто відповідає критерію Гурвіца або Найквиста при всіх [0; k].
Критерій Попова. Нелінійна система, показана на рис.3, є абсолютно стійкою, якщо виконані зазначені вище умови а) # 150; в), і при всіх [0,] виконується нерівність:
тут # 150; довільне число. ■
Критерій Попова є достатньою.
Геометрична форма критерію Попова. Для графічного дослідження системи на абсолютну стійкість будують годограф Попова. який визначається за формулою:
Тут () і () # 150; речова і уявна частини. тобто = () + (). Нагадаємо, що саме по будується годограф Найквіста для лінійної частини системи, показаної на рис 3. Для прикладу на рис. 4 показані годографи Попова і Найквиста. для однієї і тієї ж системи.
Графічний варіант критерію Попова полягає в наступному: Якщо через точку можна провести пряму так, щоб годограф Попова розташовувався повністю праворуч від неї, то система абсолютно стійка. ■
На рис. 5 показані годографи Попова, побудовані для абсолютно стійкої системи (рис. 5, а) і системи не є абсолютно стійкою (рис. 5, б).
Шляхом дослідження годографа Попова встановлено [25. С. 185], що якщо лінійна частина системи являє собою послідовне з'єднання інерційних ланок і не більше одного інтегруючого ланки, то відповідний годограф Попова буде опуклим (рис. 5, б). При цьому граничне значення при якому система абсолютно стійка за критерієм Попова, буде збігатися зі значенням. даються критерієм стійкості Найквіста, якщо нелінійність замінити прямий. Тому, якщо лінійна частина нелінійної системи має зазначений вид, то для дослідження абсолютної стійкості можна застосовувати критерій Найквіста замість критерію Попова.
Приклад 1. Дослідити на абсолютну устойчи? С- систему, схема якої показана на рис. 6.
Нелінійність належить сектору [0; 10], тобто [0; 10].
Рішення. Для вирішення завдання побудуємо годограф Попова. Для цього спочатку виділимо речову і уявну частини. маємо
Переймаючись значеннями частоти. складемо таблицю 1.
Відповідний годограф Попова побудований на рис. 7. Як видно, в даному випадку можна провести пряму через точку (# 150; 0,1; j 0) так, що годограф Попова буде розташовуватися праворуч від неї. Отже, розглядають? Ріва система абсолютно стійка. ■
Приклад 2. Дослідити на абсолютну стійкість систему, структурна схема якої показана на рис. 3, а передавальна функція лінійної частини
Нелінійність [0; 5], тобто k = 5.
Рішення. Так як лінійна частина являє собою послідовно? Тельное з'єднання інерційних ланок, то для ре? Шення завдання можна скористатися критерієм Найквіста. На рис. 8 показаний загальний вигляд розташування годографа Найквіста для систем з функцією передачі заданий? Ного виду.
Очевидно, для вирішення завдання в даному випадку досить порівняти зна? Чення з величиною при k = 5. Тому запишемо і знайдемо частоту. маємо
Прирівнюючи уявну частину знаменника в цьому виразі до нуля, підлозі? Чим
Звідси. Тоді. Умова (5), відповідно до рис. 8, виконується, якщо. тобто якщо. Отже, розглянута система абсолютно стійка при. ■
Не важко бачити, що якщо лінійна частина нелінійної системи являє собою послідовно? Тельное з'єднання інерційних ланок і одного інтегруючого ланки, то дослідження абсолютної стійкості значно спрощується, так як замість критерію Попова можна застосовувати критерій Найквіста.
3. Дослідження абсолютної стійкості при нестійкій лінійної частини
Всі відомі критерії абсолютної стійкості сформульовані для випадку, коли лінійна частина системи асимптотично стійка. Тому при нестійкій лінійної частини для забезпечення можливості застосування критеріїв абсолютної стійкості, необхідно спочатку перетворити систему так, щоб лінійна частина перетвореної системи була стійкою. Для цієї мети зазвичай застосовують додаткову зворотний зв'язок.
Розглянемо, наприклад, систему, схема якої приведена на рис. 9, а [25], де передавальна функція
а нелінійність відноситься до класу [0,2; 6], тобто
Знайти умови, при яких дана система абсолютно стійка.
Лінійна частина в даному випадку нестійка, тому введемо додаткові зв'язку з коефіцієнтом передачі. як показано на рис. 9, а. Так як введені зв'язку компенсують один одного, то отримана схема еквівалентна вихідної. Потім перенесемо вхід позитивного зворотного зв'язку з виходу системи на вихід порівнює елемента, як показано на рис. 9, б. Через перенесення через порівнює елемент цей зв'язок стане негативною, але результуюча система буде, як і раніше, еквівалентна вихідної.
Передавальна функція з урахуванням (6) і нелінійність еквівалентної схеми (рис. 9, в) визначаються за формулами
Очевидно в даному випадку
Так як система з () (7) повинна бути стійкою, то розглянута система може бути абсолютно стійкою, якщо тільки і.
Маючи на увазі застосування критерію Попова, приймемо. Тоді. а з умови слід нерівність або.
В даному випадку порядок лінійної частини дорівнює двом, тому при і годограф Попова буде розташовуватися в четвертому і третьому квадранті, як показано на рис. 7. При цьому пряму Попова через точку (# 150; 1 / 5,8; j 0) можна завжди провести так, що критерій Попова буде виконуватися.
Отже, розглянута система буде абсолютно стійка при і.
4. Круговий критерій Воронова
Критерій Воронова дозволяє досліджувати абсолютну стійкість, коли нелінійність задовольняє умовам:
Визначення. Якщо () [k 1; k 2], і виконується умова
де. то лінійна система абсолютно стійка. ■
Графічно умова (8) критерію Воронова полягає в тому, що для абсолютної стійкості нелінійної системи досить, щоб годограф Найквіста лінійної частини системи (рис. 3) не «заходив» в заборонену область, як показано на рис. 10 і рис. 11 # 150; 13. На рис. 10 ця область є кругом і показана штрихуванням.
На рис. 10 # 150; 13 заштриховані "заборонені області" як для нелінійності (а), так і для годографа Найквіста лінійної частини системи (б), відповідно.
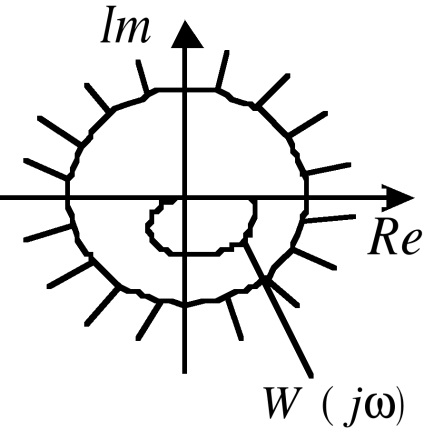
Круговий критерій Воронова простіше в застосуванні, але дає більш жорсткі ( «більш достатні») умови абсолютної стійкості. Тому його доцільно застосовувати, коли або. тобто в тих випадках, коли неможливо застосувати критерій Попова.
5. робастний стійкість
Абсолютна стійкість, як зазначалося вище, пов'язана з прагненням врахувати невизначеності, що виникають при описі нелинейностей, що входять в моделі динамічних систем. Однак в загальному випадку лінійні елементи також можуть містити невизначеності, оскільки параметри їх моделей також визначаються з деякими похибками. У зв'язку з цим вводиться, так звана, робастний стійкість систем управління.
Невизначеності у визначенні параметрів системи, таких як постійні часу або коефіцієнти передачі призводять до того, що точні значення цих параметрів виявляється невідомою. Фактично, завжди відомо лише, що значення цих параметрів лежать в деяких межах. Підкреслимо, що самі коефіцієнти. постійні часу і інші параметри системи вважаються при цьому постійними.
Це призводить до того, що в відношенні, наприклад, коефіцієнтів характеристичного полінома і інших параметрів різних моделей системи управління відомими виявляються лише інтервали, в яких лежать їхні значення.
Наприклад, коефіцієнти характеристичного полінома
лінійної системи можуть бути задані співвідношеннями
Задані таким способом коефіцієнти називаються інтервальними, а різниця # 150; інтервалом. Верхні і нижні значення розраховуються за верхнім. і нижнім. значенням коефіцієнтів. методами інтервальної математики [22].
Зазвичай інтервальний поліном -го порядку записується в такий спосіб
У технічних додатках різні похибки, невизначеності найчастіше визначаються відносною похибкою. Тому і коефіцієнти характеристичного полінома часто задаються своїми розрахунковими значеннями. знайденими з деякою відносною похибкою%, тобто При такому завданні коефіцієнтів їх верхні і нижні значення визначаються очевидними співвідношеннями:
У зв'язку з цим в подальшому будемо вважати, що задані верхні і нижні значення коефіцієнтів характеристичного полінома (11) досліджуваної системи управління. Відносні похибки% можуть бути однаковими для всіх коефіцієнтів, тобто
Визначення. Динамічна система з характеристичним поліномом (11) є робастний стійкою. якщо вона є асимптотично стійкою в цілому за будь-яких значеннях постійних коефіцієнтів. з інтервалів (10).
Для оцінки робастної стійкості систем з інтервальними параметрами зазвичай використовується критерій, запропонований В.Л. Харитоновим [22]. Цей критерій дозволяє звести задачу дослідження робастної стійкості динамічних систем до задачі дослідження гурвіцевості деяких полиномов. З цією метою спочатку складаються чотири полінома Харитонова такого вигляду:
Кожен з цих поліномів має ступінь, рівну ступеня інтервального полінома (11), а їх коефіцієнти рівні граничним значенням інтервальних коефіцієнтів цього полінома.
Критерій Харитонова. Динамічна система з інтервальним характеристичним поліномом (11) є робастний стійкою, якщо всі чотири полінома Харитонова (13) є гурвіцевимі. ■
Таким чином, для дослідження робастної стійкості деякої системи з інтервальними параметрами. необхідно знайти інтервальний характеристичний поліном цієї системи у формі (11), потім скласти чотири полінома Харитонова (13) і перевірити чи задовольняють вони критерієм Гурвіца або Рауса.
Приклад 3. Дослідити робастний стійкість системи з характеристичним поліномом
Рішення. Поліноми Харитонова в даному випадку мають вигляд
В даному випадку ступеня поліномів Харитонова. Тому
замість критерію Гурвіца можна скористатися критерієм асимптотичної стійкості Вишнеградський.
Нагадаємо, що відповідно до критерію Вишнеградський поліном третього ступеня є гурвіцевим, якщо всі його коефіцієнти більше нуля, і твір його «середніх» коефіцієнтів більше твори «крайніх» коефіцієнтів.
Застосовуючи цей критерій до поліномами (14), знайдемо, що в даному випадку всі чотири полінома Харитонова (14) є гурвіцевимі. Отже, розглянута система є робастний стійкою. ■
Розглянемо на конкретному прикладі завдання оцінки робастної стійкості системи 3-го порядку при завданні відносної точності настройки її параметрів.
Приклад 4. Оцінити робастний стійкість системи з характеристичним поліномом
при 5% і 2% похибки реалізації його коефіцієнтів.
Рішення. При точних (розрахункових) значеннях коефіцієнтів дана система, очевидно, є асимптотично стійкою. Дійсно, всі коефіцієнти полінома (15) більше нуля, а твір його «середніх» коефіцієнтів одно 186, що більше твори «крайніх» коефіцієнтів, рівного 160. Тому відповідно до критерію Вишнеградський система стійка.
При реалізації коефіцієнтів з похибкою 5% відповідно (12) граничні значення інтервалів рівні:
Отже, інтервальний поліном даної системи в даному випадку має вигляд
а відповідні поліноми Харитонова
В даному випадку перший, другий і четвертий поліноми задовольняють критерію Вишнеградський, а третій # 150; не задовольняє, так як 2,8558,9 = 167,865, а 8,421 = 176,4.
Таким чином, при реалізації коефіцієнтів з похибкою 5% розглянута система не є робастний стійкою.
При реалізації коефіцієнтів з похибкою 2% граничні значення інтервалів рівні:
а відповідні поліноми Харитонова
При цьому нерівності критерію Вишнеградський мають вигляд: 185,93> 159,94; 185,93> 159,94; 178,63> 166,46; 193,15> 153,64.
Таким чином, при реалізації коефіцієнтів з похибкою 2% все чотири полінома Харитонова відповідають критеріям Вишнеградський, тобто в цьому випадку розглянута система є робастний стійкою.
Відсутність в Англії яскраво вираженою епохи абсолютизму як наприклад у Франції; існування парламенту на всьому протязі англійського абсолютизму; компромісний і незавершений характер англійської буржуазної революції ХУПв .; наступність у розвитку державних інститутів дозволили буржуазним історикам і державознавець віднести виникнення конституційного ладу в Англії до XIII ХУ століть заперечувати наявність періоду абсолютизму в країні розглядати англійську буржуазну революцію ХУП в. f як констітуціоннорелігіозний конфлікт.
Властивість системи приходити в початковий стан після зняття обурення називається стійкістю. Критерій стійкості - це правило, що дозволяє з'ясувати стійкість системи без обчислення коріння характеристичного рівняння.