Теорія взаємного розташування прямих і площин в просторі грунтується на наступних аксіомах.
Аксіома 1. Якщо три точки не лежать в одній прямий, то через них проходить єдина площина.
Аксіома 2. Якщо дві точки прямої лежать в площині, то кожна точка цієї прямої належить площині. У цьому випадку говорять, що пряма лежить в площині.
Аксіома 3. Якщо дві площини мають спільну точку, то вони мають і загальну пряму, що проходить через цю точку.
Властивість площині, яку фіксує аксіома 1, часто використовується на практиці. Вістря ніжок штатива фотоапарата належать одній площині, і тому її положення стійке. Двері, закріплені на двох петлях, не займають певного положення, але якщо додати третю точку кріплення - замок, то становище дверей фіксується. Коли ніжки табурета підрізані неправильно, то табурет стоїть на трьох ніжках, а четверта ніжка висить над підлогою.
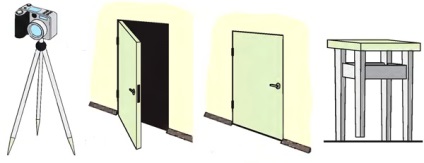
Властивість площині. яке виражає аксіома 2, використовують для перевірки прямолінійності креслярської лінійки. Лінійку прикладають краєм до поверхні столу: якщо край прямолінійний, то він усіма своїми точками прилягає до поверхні столу, а якщо нерівний, то між краєм лінійки і поверхнею столу є щілина.
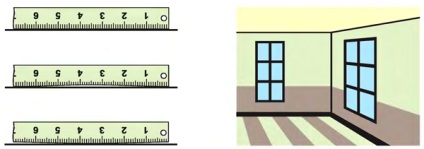
Властивість площині, зафіксоване аксіомою 3, проявляється при перетині суміжних стін кімнати.
Відзначимо, що в стереометрії залишаються дійсними всі аксіоми планіметрії і все доведені в ній твердження. Зокрема, ознаки рівності і ознаки подібності трикутників залишаються в силі і для трикутників, що лежать в різних площинах. Відповідно до аксіомою 1 площину визначається трьома своїми точками А, В, С, тому іноді площину позначають трьома великими латинськими буквами: площину, що проходить через точки А, В, С, позначають ABC.