Алгоритми Сортування. Частина 1
Все з існуючих нині способів сортування відрізняються один від одного за швидкістю виконання, зрозумілості і довжині коду, за красою рішення. Найчастіше в код вже розробленого алгоритму вносяться певні зміни і так виникає безліч рішень, деякі і з яких ми і спробуємо зараз розглянути.
Однак, слід зазначити що вивчення алгоритмів зовсім не легке завдання, тут потрібно уважний розгляд кожного рядка. Звичайно якщо Ви скористаєтеся кнопками Ctrl + C і Ctrl + V Ваша програма не стане гірше працювати, але на мій погляд, немає нічого гіршого коли програміст сам до кінця не розуміє, як працює його програма.
Сортування вибором
І почнемо ми з сортування вибором. Хоча цей алгоритм і не є найшвидшим, але я вирішив почати з нього бо, на мій погляд він найбільш простий для розуміння. Суть алгоритму полягає в тому, що б у вихідному масиві знайти найменший елемент, а потім поміняти місцями перший елемент в списку зі знайденим. Після того, перебувати найменший їх залишилися і змінюється з другим елементом. І так до тих пір поки весь перелік не буде відсортований.
Таким чином знадобитися N + (N-1) + (N-2) +. +1 або N * N проходів щоб впорядкувати список.
Лістинг 1. Сортування вибором
Змінними min і mах можна обмежити область списку в якій, буде виконана сортування. Що б впорядкувати весь масив необхідно записати наступне
Лістинг 2. Код Delphi / Pascal
SellectionSort (a, 0, high (a));
Сортування вставкою
Це теж гранично простий для розуміння алгоритм. Ідея в тому щоб створити новий масив, а потім послідовно вставляти в новий масив елементи зі старого масиву, щоб створений масив був весь час впорядкованим.
Лістинг 3. Сортування вставкою
Якщо уважно подивитися на реалізацію алгоритму, то відразу ж зауважимо що для його виконання необхідно більше. ніж N * N проходів, тому в додатках, де швидкість виконання коду критична, подібний алгоритм використовувати не актуальне.
бульбашкова сортування
Найчастіше використовується для сортування частково впорядкованих списків, так як саме для них швидкість виконання максимальна і може дорівнювати O (N), де N кількість елементів масиву, а O час одного проходу через цикл. Цей алгоритм в вихідному списку шукає пари чисел, які слідують не по порядку і потім змінює їх местамі.Процесс повторюється до тих пір поки весь перелік не буде відсортованим. На малюнку зображено приклад сортування даним методом.
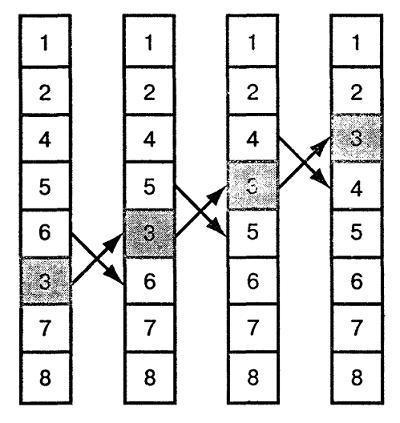
На малюнку можна простежити за переміщення елемента, який спочатку був нижче ніж після сортування. Під час проходу циклу, елемент змінює свою позицію на одну позицію ближче до свого кінцевого місця. На малюнку елемент рухається до вершини, як бульбашка повітря до поверхні води. Цей ефект і дав назву алгоритму бульбашкового сортування.
Лістинг 4. Бульбашкова сортування
Швидке сортування.
При цьому виді сортуванні масив розбивається на дві частини, а потім рекурсивно викликає сама себе для їх сортування. Притому елементи першої частини менше будь-якого елементу другої частини.
Погляньмо на цей вид сортування на прикладі:
Якщо алгоритм викликається для списку, який містить нуль або один елемент, то підписок вже відсортований і процедура закінчується, в іншому випадку вибирається один елемент, щодо якого список розбивається на дві частини, в перший підписок йдуть елементи менше обраного, в другій більше. І потім, як уже було сказано, вона рекурсивно викликає сама себе для сортування шпалери подсписков.
Лістинг 5. Швидке сортування
Варто також зауважити, що такий сортуванням найкраще користуватися для упорядочеванія масивів елементи в яких слідують абсолютно, випадково. У той час як, якщо список практично впорядкований, розумніше буде використовувати бульбашкову сортування. До того ж якщо список досить довгий, то алгоритм викличе глибоку рекурсію і з обсягом стёка і як наслідок зависання або аварійний вихід програми.
Сортування методом Шелла.
Ще один метод сортування - це сортування методом Шелла.Основная ідея цього алгоритму полягає в тому, щоб на початку ycтpаніть масовий безлад в масиві, порівнюючи далеко стоять один від одного елементи. Як видно, інтервал між порівнюваними елементами поступово зменшується до одиниці. Це означає, що на пізніх стадіях сортування зводиться просто до перестановок сусідніх елементів (якщо, звичайно, такі перестановки є необхідними).
Лістинг 6. Сортування методом Шелла
Висновок.
P.S. Зауваження, побажання та доповнення до цієї статті просимо залишати на форумі.