Дискретна випадкова величина Х розподілена за біноміальним законом, якщо вона може набувати значень 0, 1, 2, ..., n
з вірогідністю, які знаходяться за формулою Бернуллі:
Приклад. Нехай проводиться довільне витяг трьох словоформ з науково-технічного тексту. Вважаючи, що ймовірність вживання іменника в науково-технічному тексті дорівнює 0,4, для СВ Х # 8209; «Число вибраних іменників», знайти математичне сподівання М (Х) і дисперсію D (Х).
Рішення. СВ Х розподілена за біноміальним законом, так як випробування є незалежними, а ймовірність появи іменника в кожному з трьох випробувань постійна.
Тут n = 3, р = 0,4, q = 1-р = 0,6. Тоді М (Х) = n р = 3 0,4 = 1,2; D (Х) = n р q = 3 0,4 0,6 = 0,72.
Дискретна випадкова величина Х розподілена за законом Пуассона, якщо вона може набувати значень 0, 1, 2, ..., n
з вірогідністю, які знаходяться за формулою Пуассона:
Приклад. Імовірність появи помилки на кожній сторінці текта, що містить 200 сторінок, дорівнює 0,01. визначити:
а) ймовірність появи трьох помилок в тексті;
б) математичне сподівання М (Х) і дисперсію D (X) СВ Х = «кількість помилок в тексті».
Рішення. Так як помилка - рідкісна подія (р = 0,01), то скористаємося формулою Пуассона для знаходження ймовірностей рідкісних подій:
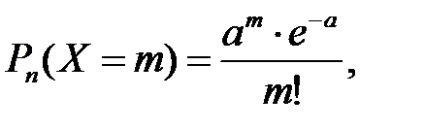
б) Випадкова величина Х - «кількість помилок в тексті» розподілено згідно із законом Пуассона, для якого М (Х) = D (X) = а = 0,2.