Грецькі математики займалися в основному геометрією і багато часу проводили підраховуючи кількість точок, розташованих на площині у формі різних геометричних фігур. Кількість точок, які складають
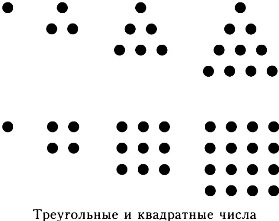
Можна уявити собі сверхмікроскопіческій трикутник, що складається з однієї точки. Три точки також утворюють трикутник, у якого по дві точки на кожній стороні. Шість точок утворюють вже більший трикутник, у якого по три точки на кожній стороні, а десять точок - трикутник, у якого по чотири точки на кожній стороні.
Можна записати трикутні числа в ряд: 1, 3, 6, 10, 15, 21. 28, 36, 45, 55 і так далі. Кожне наступне трикутне число утворює трикутник, у якого на кожній стороні на одну точку більше. Ряд трикутних чисел можна продовжувати нескінченно.
Зверніть увагу, ряд трикутних чисел утворює певну залежність. Перше число дорівнює 1, наступне дорівнює 3, тобто 1 + 2, потім йде 6, тобто 1 + 2 + 3, потім 10, тобто 1 + 2 + 3 + 4, потім 15, тобто 1 + 2 + 3 + 4 + 5, і так далі. Запам'ятавши цю залежність, ви зможете продовжувати ряд трикутних чисел як завгодно довго, не складаючи трикутників і не перераховуючи точки. Визначити, чи є дане число трикутним чи ні, можна, представивши його у вигляді ряду, подібного до наведеного вище. Якщо число можна представити у вигляді суми чисел, де кожне наступне число на одиницю більше попереднього, а перше число є одиницею, то це число - трикутне.
Будь-яка група чисел, яка може бути представлена у вигляді послідовності, що підкоряється якомусь правилу, утворює числовий ряд.
Числа, які є кількістю точок, з яких можна скласти квадрат, теж можна представити у вигляді ряду. Як і минулого разу, одну точку можна розглядати як сверхмікроскопіческій подружжя
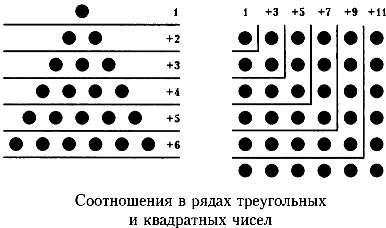
Можна записати чотирикутні числа в ряд: 1, 9, 16, 25, 36, 49 і так далі. Кожне наступне чотирикутне число утворює чотирикутник, у якого на кожній стороні на одну точку більше. Ряд чотирикутних чисел можна продовжувати нескінченно.
Проаналізувавши числа, складові ряд чотирикутних чисел, ми побачимо, що вони теж підпорядковуються певній залежності. Почнемо з 1. Тут немає варіантів, одиниця - це просто одиниця. Але вже 4 = 1 + 3, далі 9 = 1 + 3 + 5, 16 = 1 + 3 + 5 + 7 і так далі.
Співвідношення між числами треуголь-ного і квадратного рядів показано на діаграмі.
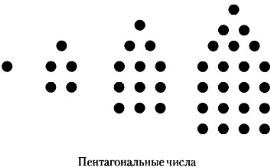
У греків був також ряд пентагональні чисел. які представлені на малюнку. Цей ряд можна розглядати як якийсь синтез трикутних і чотирикутних рядів. Якщо ми побудуємо кілька п'ятикутників таким же чином, як будували трикутники і чотирикутники, то отримаємо числовий ряд виду 1, 5, 12, 22, 35, 51, 70 і так далі. Це ряд чисел, які отримують складанням чисел, що відрізняються один від одного на три. Перший член ряду - це одиниця. Другий - 5, тобто 1 + (1 + 3) = 1 + 4. Третій - 12, тобто 1 + 4 + (4 + 3) = 1 + 4 + 7, четвертий - 22, тобто 1 + 4 + 7 + 10, і так далі.
Греки винайшли і інші геометричні фігури. моделюють числові ряди. Числа, що складають такі послідовності, називаються фігурними. Деякі фігурні числа моделюються вже не плоскими фігурами, як трикутник і квадрат, а об'ємними, наприклад кубами. Такі куби важко зобразити на малюнку, але якщо ви уважно подивитеся на числовий ряд, ви зможете скласти собі якесь уявлення про кубічної фігурі з точок. Серія кубічних чисел - це ряд 1, 8, 27, 64, 125 і так далі.
Ряд кубічних чисел також є ряд сум непарних чисел. правда, ці суми не починаються з одиниці. Перший член ряду - це 1, другий - 8 або 3 + 5; третій - це 27 або 7 + 9 + 11; четвертий - це 64 або 13 + 15 + 17 + 19. Кожна група чисел, які треба підсумовувати, починається з непарного числа, наступного за тим, яке завершувало попередню суму, а кількість доданків у кожній наступній сумі на одне більше, ніж у попередній.
Матеріали по темі:
Поділитися з друзями: