Деякі властивості визначників

Попередня ↔ Наступна

Тут будуть викладені ті властивості, які зазвичай використовуються для обчислення визначників в стандартному курсі вищої математики. Це допоміжна тема, до якої будемо звертатися з інших розділів в міру необхідності.

Отже, нехай задана деяка квадратна матриця $ A _ = \ left (\ begin a_ a_ \ ldots a_ \\ a_ a_ \ ldots a_ \\ \ ldots \ ldots \ ldots \ Ldots \\ a_ a_ \ ldots a_ \\ \ end \ right) $. Кожна квадратна матриця має характеристикою, яка називається визначником (або детермінантом). Я не вдаватимуся тут в суть цього поняття. Якщо воно вимагає пояснень, то прошу відписати про це на форум. і я торкнуся цього питання детальніше.

Позначається визначник матриці $ A $ як $ \ Delta A $, $ | A | $ або $ \ det A $. Порядок визначника дорівнює кількості рядків (стовпців) в ньому.

Значення визначника не зміниться, якщо його рядки замінити відповідними стовпцями, тобто $ \ Delta A = \ Delta A ^ T $.

Приклад застосування цієї властивості: показати \ приховати

Розглянемо визначник $ \ left | \ Begin 2 5 \\ 9 4 \ end \ right | $. Знайдемо його значення, використовуючи формулу №1 з теми обчислення визначників другого і третього порядків.

$$ \ left | \ Begin 2 5 \\ 9 4 \ end \ right | = 2 \ cdot 4-5 \ cdot 9 = -37. $$

Замінимо в ньому рядки стовпцями за принципом: "була перший рядок - став перший стовпець", "була другий рядок - став другий стовпець":

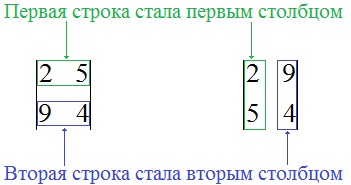
Обчислимо отриманий визначник: $ \ left | \ Begin 2 9 \\ 5 4 \ end \ right | = 2 \ cdot 4-9 \ cdot 5 = -37 $. Як бачите, значення визначника від проведеної заміни не змінилося.

Якщо поміняти місцями два рядки (стовпці) визначника, то знак визначника зміниться на протилежний.

Приклад застосування цієї властивості: показати \ приховати

$$ \ left | \ Begin 2 5 \\ 9 4 \ end \ right | = 2 \ cdot 4-5 \ cdot 9 = -37. $$

Тепер поміняємо місцями першу і другу рядки. Отримаємо визначник $ \ left | \ Begin 9 4 \\ 2 5 \ end \ right | $. Обчислимо отриманий визначник: $ \ left | \ Begin 9 4 \\ 2 5 \ end \ right | = 9 \ cdot 5-4 \ cdot 2 = 37 $. Отже, значення вихідного визначника дорівнювало (-37), а у визначника зі зміненим порядком рядків значення дорівнює $ - (- 37) = 37 $. Знак визначника змінився на протилежний.

Визначник, у якого всі елементи рядка (стовпчика) дорівнюють нулю, дорівнює нулю.

Приклад застосування цієї властивості: показати \ приховати

Так як в визначнику $ \ left | \ Begin -7 10 0 \\ -9 21 0 \\ 2 -3 0 \ end \ right | $ всі елементи третього стовпця дорівнюють нулю, то визначник дорівнює нулю, тобто $ \ Left | \ Begin -7 10 0 \\ -9 21 0 \\ 2 -3 0 \ end \ right | = 0 $.

Визначник, у якого всі елементи якоїсь рядки (стовпці) рівні відповідних елементів іншого рядка (стовпця) дорівнює нулю.

Приклад застосування цієї властивості: показати \ приховати

Так як в визначнику $ \ left | \ Begin -7 10 0 \\ -7 10 0 \\ 2 -3 18 \ end \ right | $ всі елементи першого рядка дорівнюють відповідним елементам другого рядка, то визначник дорівнює нулю, тобто $ \ Left | \ Begin -7 10 0 \\ -7 10 0 \\ 2 -3 18 \ end \ right | = 0 $.

Якщо у визначнику всі елементи одного рядка (стовпця) пропорційні відповідним елементам іншого рядка (стовпця), то такий визначник дорівнює нулю.

Приклад застосування цієї властивості: показати \ приховати

Так як в визначнику $ \ left | \ Begin -7 10 28 \\ 5 -3 0 \\ -15 9 0 \ end \ right | $ другий і третій рядки пропорційні, тобто $ III = -3 \ cdot II $, то визначник дорівнює нулю, тобто $ \ Left | \ Begin -7 10 28 \\ 5 -3 0 \\ -15 9 0 \ end \ right | = 0 $.

Якщо всі елементи рядка (стовпчика) мають загальний множник, то цей множник можна винести за знак визначника.

Приклад застосування цієї властивості: показати \ приховати

Розглянемо визначник $ \ left | \ Begin -7 10 \\ -9 21 \ end \ right | $. Зауважте, що всі елементи другого рядка діляться на 3:

$$ \ left | \ Begin -7 10 \\ -9 21 \ end \ right | = \ left | \ Begin -7 10 \\ 3 \ cdot (-3) 3 \ cdot 7 \ end \ right | $$

Число 3 і є загальний множник всіх елементів другого рядка. Винесемо трійку за знак визначника:

Визначник не зміниться, якщо до всіх елементів якоїсь рядки (стовпці) додати відповідні елементи іншого рядка (стовпця), помножені на довільне число.

Приклад застосування цієї властивості: показати \ приховати

Розглянемо визначник $ \ left | \ Begin -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | $. Додамо до елементів другого рядка відповідні елементи третього рядка, помножені на 5. Записують це так:

$$ \ left | \ Begin -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | \ Begin \ phantom \\ II + 5 \ cdot III \\ \ phantom \ end $$

Другий рядок буде змінена, інші рядки залишаться без змін.

Якщо у визначнику якась рядок (стовпець) є лінійна комбінація інших рядків (стовпців), то визначник дорівнює нулю.

Приклад застосування цієї властивості: показати \ приховати

Відразу поясню, що означає словосполучення "лінійна комбінація". Нехай у нас є s рядків (або стовпчиків): $ A_1 $, $ A_2 $. $ A_s $. вираз

$$ k_1 \ cdot A_1 + k_2 \ cdot A_2 + \ ldots + k_s \ cdot A_s, $$

де $ k_i \ in R $ називається лінійною комбінацією рядків (стовпців) $ A_1 $, $ A_2 $. $ A_s $.

Для прикладу розглянемо такий визначник:

$$ \ left | \ Begin -1 2 3 0 \\ -2 -4 -5 1 \\ 5 0 7 10 \\ -13 -8 -16 -7 \ end \ right | $$

У цьому визначнику четвертий рядок можна виразити як лінійну комбінацію перших трьох рядків:

$$ IV = 2 \ cdot I + 3 \ cdot II-III $$

Отже, розглянутий визначник дорівнює нулю.

Якщо кожен елемент якоїсь k-го рядка (k-го стовпця) визначника дорівнює сумі двох доданків, то такий визначник дорівнює сумі визначників, у першого з яких в k-му рядку (k-му стовпці) стоять перші доданки, а у другого визначника в k-му рядку (k-му стовпці) розташовані другі доданки. Інші елементи цих визначників однакові.

Приклад застосування цієї властивості: показати \ приховати

Розглянемо визначник $ \ left | \ Begin -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | $. Запишемо елементи другого стовпця так: $ \ left | \ Begin -7 3 + 7 0 \\ -9 21 + 0 4 \\ 2 5 + (- 8) 1 \ end \ right | $. Тоді такий визначник дорівнює сумі двох визначників:

Визначник добутку двох квадратних матриць одного порядку дорівнює добутку визначників цих матриць, тобто $ \ Det (A \ cdot B) = \ det A \ cdot \ det B $. Узагальнення цього правила: $ \ det \ left (A ^ n \ right) = \ left (\ det A \ right) ^ n $.

Якщо матриця $ A $ - невироджена (тобто її визначник не дорівнює нулю), то $ \ det \ left (A ^ \ right) = \ frac $.

Формули для обчислення визначників

Для визначників другого і третього порядків вірні такі формули:

Визначник матриці $ A_ $ можна розкласти по i-му рядку, використовуючи наступну формулу:

Аналог цієї формули існує і для стовпців. Формула для розкладання визначника по j-му стовпцю виглядає наступним чином:

Зазначимо ще одну формулу для обчислення визначників верхніх трикутних і нижніх трикутних матриць (пояснення цих термінів см. В темі "Матриці. Види матриць. Основні терміни"). Визначник такої матриці дорівнює добутку елементів, що стоять на головній діагоналі. приклади:

\ begin \ Left | \ Begin 2 -2 9 1 \\ 0 9 8 0 \\ 0 0 4 -7 \\ 0 0 0 -6 \ end \ right | = 2 \ cdot 9 \ cdot 4 \ cdot (-6) = - 432. \\ \ Left | \ Begin -3 0 0 0 \\ -5 0 0 0 \\ 8 2 1 0 \\ 5 4 0 10 \ end \ right | = -3 \ cdot 0 \ cdot 1 \ cdot 10 = 0. \ end

Деякі властивості визначників

Формули для обчислення визначників

Схожі статті