Якщо взяти всі активи, присутні на ринку, і всі можливі їх комбінації (портфелі), на площині «прибутковість - ризик» отримаємо деяку множину, подібне до того, яке зображено на рис. 7.6. Що огинає його крива називається ефективної кордоном. Завдяки позитивному впливу диверсифікації в повному обсязі корелюється активів, точки на ефективної кордоні будуть відповідати не індивідуальним активів, а портфелям (можливі виключення - актив з максимальною очікуваною прибутковістю і актив з мінімальним ризиком). Справді, при об'єднанні в портфель кожної пари активів лінія на площині «прибутковість - ризик», відповідна різних співвідношеннях ваг, буде проходити лівіше і вище прямої, що з'єднують відповідні точки, при об'єднанні пар таких портфелів в новий портфель - ще лівіше і вище, і т.д. а ефективна межа буде обвідної безлічі всіх таких ліній.
Мал. 7.6. Ефективна межа як огинає безлічі ризикованих портфелів
Підвищення прибутковості спричиняє підвищення ризику, але тільки при русі вздовж ефективної кордону. Якщо ж портфель лежить нижче ефективної кордону, то за рахунок додаткової диверсифікації можна підвищити його прибутковість, не підвищуючи ризик. Протилежне твердження «підвищення ризику тягне зростання прибутковості» - невірно - ринок винагороджує зовсім не всякий ризик, і завжди можна знайти актив з високим ризиком і низькою (а то і негативною) прибутковістю.
Кожна точка ефективної кордону відповідають ефективному портфелю. Портфель є ефективним, якщо жоден інший портфель не забезпечує більш високу очікувану прибутковість при тому ж рівні очікуваного ризику, або нижчий ризик при тому ж рівні прибутковості.
Вибір ефективного портфеля залежить від схильності інвестора до ризику. Схильність до ризику прийнято характеризувати так званої «функцією корисності» (utility function). Ця функція будується в припущенні, що з ростом ризику інвестор вимагає все більшого і більшого зростання прибутковості (така поведінка інвесторів підтверджується емпіричними спостереженнями). На площині «прибутковість-ризик» функція корисності кожного інвестора відображається сімейством кривих другого порядку, кожна з яких складається з точок, так само «корисних», а «корисність» збільшується при зсуві кривих вліво-вгору.
Мал. 7.7. Вибір оптимального портфеля на ефективної кордоні за допомогою функції корисності інвестора.
У ефективної кордону в міру збільшення ризику нахил зменшується - відбувається насичення. Справді, ризикованість активу може рости хоч до безкінечності - оскільки інвестори уникають ризику, такі активи завжди знайдуться. А ось за високою прибутковістю інвестори полюють, і активи з аномально високою прибутковістю до ринку просто не доходять. Таким чином, реалізується положення, показане на рис. 7.7, де наведені ефективна межа і сімейства функцій корисності для двох інвесторів. Криві U уособлюють переваги інвестора, несхильність до ризику - вони круто йдуть вгору (за приріст ризику інвестор вимагає набагато більшого приросту прибутковості). Криві V відносяться до інвестора, більш терпимого до ризику.
Криві з індексом 1 перетинають ефективну кордон в двох точках, отже, кожному інвестору можна сформувати два портфеля, суб'єктивно рівноцінних - більший ризик другого портфеля буде повністю компенсуватися більшою прибутковістю. Однак більш високу корисність (або задоволеність) кожен інвестор може здійснити при якомусь середньому портфелі, а саме там, де функція корисності стосується ефективної кордону (криві з індексом 2) - така точка тільки одна для кожного інвестора (що характеризується своєю функцією корисності). Ще більшу задоволеність інвестори відчували б на кривих з індексом 3, але на жаль - вони не перетинаються з ефективною кордоном, і портфелів з такою «корисністю» сформувати не можна. Отже, оптимальним портфелем буде той, для якого функція корисності стосується ефективної кордону - він одночасно є і ефективним, і найбільш «корисним» для даного інвестора.
Коефіцієнт кореляції rij - це статистична міра напрямки і ступеня лінійної залежності між двома випадковими змінними (змінюється від -1 до +1). Для різних значень коефіцієнта кореляції на рис. 7.8 наведені відповідні діаграми розсіювання. При нульовій кореляції змінні X і Y ніяк не пов'язані - Y змінюється цілком випадково, незалежно від змін X.
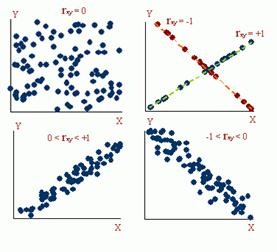
Мал. 7.8. Діаграми розсіювання при різних значеннях коефіцієнта кореляції.
При наближенні абсолютної величини коефіцієнта кореляції до одиниці залежність між змінними набуває все більш певний характер, до тих пір, поки випадковість повністю усувається (діаграма в правому верхньому куті). На діаграмі в лівому нижньому кутку рис. 7.8 коефіцієнт кореляції дещо вищий за абсолютною величиною, ніж на діаграмі в правому нижньому кутку - точки групуються ближче до лінії регресії.
Квадрат коефіцієнта кореляції (завжди позначається як Rij 2) називається коефіцієнтом детермінації. Цей коефіцієнт є мірою розсіювання даних щодо лінії регресії і показує, яка частка зміни залежної змінної Y визначається (детермінується) зміною незалежної змінної X.
Теорія оцінки активів (CAPM)
Теорія оцінки активів (CAPM - Capital Asset Pricing Model) є продовженням теорії ефективного портфеля. Точніше, поширенням цієї теорії на включення в ефективний портфель безризикового активу. Доповнимо портфель ризикованих активів (з індексом A) безризиковим активом (з індексом rf - risk- free), у якого за визначенням стандартне відхилення прибутковості нульове (# 963; rf = 0). Очевидно, ковариация безризикового активу з будь-яким ризикованим активом дорівнює нулю, так само, як і коефіцієнт кореляції. тоді
Таким чином, і ризик, і прибутковість об'єднаного портфеля лінійно залежать від відповідних величин для ризикованого портфеля. Тому на площині «прибутковість - ризик» залежність прибутковості об'єднаного портфеля від ризику виглядає як пряма лінія, що з'єднує безризиковий актив з будь-яким з ризикованих портфелів, що лежать на ефективної кордоні (рис. 7.9, пряма Rrf A). Для того, щоб збільшити прибутковість (а заодно і ризик) об'єднаного портфеля, потрібно збільшувати частку ризикованого портфеля по відношенню до частки безризикового активу.
Вираз, що визначає прибутковість портфеля, можна переписати у вигляді
Тут явно видно лінійна залежність між прибутковістю портфеля і стандартним відхиленням його прибутковості. Тангенс кута нахилу цієї лінії (RA - Rrf) / # 963; A відомий як коефіцієнт Шарпа.
Зрушення точки А вздовж ефективної кордону вгору-вправо збільшує ефективність об'єднаного портфеля (максимізує коефіцієнт Шарпа) - для тих же ризиків прибутковість стає все вище і вище. Однак всьому є межа - максимальна ефективність досягається тоді, коли пряма, відповідна об'єднаному портфелю, стосується ефективної кордону. Точку дотику прийнято позначати через М (market).
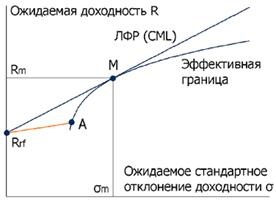
Мал. 7.9 Лінія ринку капіталу (CML)
Очевидно, з урахуванням безризикового активу нової ефективної кордоном стає пряма Rrf M (рис. 7.9), що лежить вище старої ефективної кордону (для портфелів ризикованих активів) всюди, за винятком точки дотику М. Ця пряма називається лінією ринку капіталу, скорочено ЛРК (CML - capital market line). Всі інвестори обиратимуть портфелі саме на цій прямій, відповідно до індивідуальної функцією корисності (в точці дотику функції корисності і ЛРК). Портфелі для різних інвесторів (з різним ризиком) будуть при цьому відрізнятися тільки часткою безризикового активу.
Таким чином, всі інвестори будуть купувати (в різних частках) один і той самий ризикований портфель, що відповідає точці М на ефективної кордоні. Тому портфель М повинен включати всі ризиковані активи - адже якщо актив не включений в такий портфель, це означає, що на нього немає ніякого попиту, отже, вартість його нульова. Оскільки передбачається, що ринок знаходиться в рівновазі, то необхідно, щоб всі ризиковані активи були включені в портфель М в частках, пропорційних їх ринкової капіталізації (для акцій - твір ринкової ціни акції на кількість акцій в обігу). Якщо, наприклад, частка активу в портфелі буде вище, ніж частка в капіталізації, надлишковий попит на такий актив призведе до зростання його ціни (і зростання капіталізації).
Портфель ризикованих активів, загальний для всіх інвесторів, називається ринковим портфелем. Так як він містить всі без винятку ризиковані активи, він повністю диверсифікований - все індивідуальні ризики активів повністю компенсовані. У ринковому портфелі залишається тільки систематичний ризик, джерело якого - нестабільність в макроекономіці (ось чому інвестори проявляють такий великий інтерес до даних станом економіки). Найбільш сильно впливають на систематичний ризик зміни таких показників, як ВВП, інфляція, рівень процентних ставок, а також середній по економіці рівень корпоративного прибутку.
Про те, як диверсифікувати портфель (наблизити його характеристики до характеристик ринкового портфеля), говорилося в попередньому параграфі. Тут можна додати, що систематичний (недіверсіфіціруемий) ризик ринкового портфеля часто називають ринковим ризиком. А хорошою аппроксимацией ринкового портфеля, як це випливає з визначення, є ринковий індекс, зважений за капіталізацією (не дарма ми приділили опису індексів так багато місця). Для ринку акцій США інвестори орієнтуються на індекс SP 500, Росії - індекс РТС.
У разі, якщо інвестор бажає взяти ризику більше, ніж його є в точці М (# 963; m), йому слід вкласти в ризикований портфель М грошей більше, ніж у нього є, тобто взяти кредит під відсоток, рівний Rrf. При цьому прибутковість і ризик портфеля виражаються тими ж формулами, що і раніше, тільки Wrf стає негативною. І прибутковість, і її стандартне відхилення продовжують залишатися лінійними функціями відповідних величин для ринкового портфеля, тому лінія ринку капіталу просто триває нагору. Взяття кредиту відповідає зміщення по цій лінії правіше точки М. Правда, як завгодно далеко зміститися не вдасться - регулятори ринку (SEC в США і ФКЦБ в Росії) обмежують розмір кредиту, який можна взяти у брокера під заставу вже наявного портфеля (маржинальне кредитування).
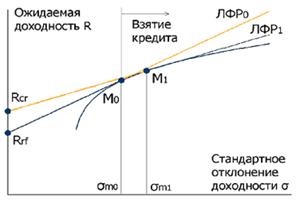
Мал. 7.10 Лінія ринку капіталу при відміну ставки кредитування від безризиковою
У реальному житті, зрозуміло, ставка кредитування вище безризиковою (часто набагато вище), і ЛРК стає ламаною лінією (рис. 7.10) - вона складається з відрізків ЛРК0 і ЛРК1. ЛРК1 будується виходячи з точки Rcr (ставка кредитування) і стосується ефективної кордону не в «старій» точці М0. а правіше і вище, в точці М1. Точка М «роздвоюється» - для інвесторів, що використовують кредитні кошти, ринковий портфель повинен бути трохи більш ризикованим, але зазвичай відмінностями нехтують. Нехтують і тим, що між точками М0 і М1 портфель повинен вибиратися на «старої» ефективної кордоні ризикованих активів, і зрозуміло, чому - дотична тут проходить дуже близько до ефективної кордоні, та й зазвичай якщо вже беруть в борг, то багато.