1. Енергія системи нерухомих точеч-них зарядів. Електростатичні сили взаємодії консервативні; отже, система зарядів володіє потенційною енергією. Знайдемо потенційну енергію системи двох точкових зарядів Q1 і Q2. знаходяться на відстані r один від одного. Кожен з цих зарядів в поле іншого володіє потенційною енергією:
де # 966; 12 і # 966; 21 - відповідно потенциа-ли, створювані зарядом Q2 в точці знаходження заряду Q1 і зарядом Q1 в точці знаходження заряду Q2. Потенціал поля точкового заряду дорівнює:
Додаючи до системи з двох зарядів по-отже заряди Q3, Q4. ..., можна переконатися в тому, що в разі nнепод-Віжн зарядів енергія взаємодії системи точкових зарядів дорівнює
де ji - потенціал, створюваний в тій точці, де знаходиться заряд Qi. усіма за-рядами, окрім i-го.
2. Енергія зарядженого відокремленого провідника. Нехай є відокремлений провідник, заряд, ємність і потенціал якого відповідно рівні Q, С, # 966 ;. Збільшимо заряд цього провідника на dQ. Для цього необхідно перенести заряд dQ з нескінченності на відокремлений провід-ник, витративши на це роботу, рівну
Щоб зарядити тіло від нульового потенци-ала до j, необхідно зробити роботу
Енергія зарядженого провідника рав-на тій роботі, яку необхідно зробити, щоб зарядити цей провідник:
Цю формулу можна отримати і з того, що потенціал провідника у всіх його точках однаковий, тому що поверхня провідника є еквіпотенціальной.Полагая потенціал провідника рівним j, з (3) знайдемо
де - заряд провідника.
3. Енергія зарядженого конденсато-ра. Як всякий заряджений провідник, конденсатор має енергію, яка відповідно до формули (4) дорівнює
де Q - заряд конденсатора, З - його їм-кістка, Dj - різниця потенціалів між обкладинками.
Використовуючи вираз (5), можна знайти механічну силу, з якою пластини кондом-сатора притягують один одного. Для цього припустимо, що відстань х між-ду пластинами змінюється, наприклад, на величину dx. Тоді діюча сила со-вершает роботу
внаслідок зменшення потенційної енергії системи
Підставивши в (5) в формулу ємності плоского конденсатора, по-лучім
Проізводядіфференцірованіе при кон-конкретного значення енергії (див. (6) і (7)), знайдемо шукану силу:
де знак мінус вказує, що сила Fявляется силою тяжіння.
4. Енергія електростатичного поля.
Перетворимо формулу (5), яка має енергію плоского конденсатора за допомогою зарядів і потенціалів, воcпользовавшісь виразом для ємності плоского конденсатора (C = e0 eS / d) і раз-ності потенціалів між його обкладинками (Dj = Ed). тоді отримаємо
де V = Sd - об'єм конденсатора. Ця форму-ла показує, що енергія кон-денсатора виражається через величину, що характеризує електростатичне по-ле, - напруженість Е.
Густина енергії електростатичного поля (енергія одиниці об'єму)
Цей вислів справедливо тільки для ізотропного діелектрика, для якого виконується співвідношення: Р = ce0 E.
Формули (5) і (8) соответствен-но пов'язують енергію конденсатора з за-поруч на його обкладках і з напружено-стю поля. Виникає, природно, питання про локалізацію електростатичної енер-гии і що є її носієм - заряди чи иоле? Відповідь на це питання може дати тільки досвід. Електростатика вивчає постійні в часі поля нерухомих зарядів, т. Е. В ній поля і зумовили їх заряди невіддільні одне від одного. По-цьому електростатика відповісти на постав-лені питання не може. Подальший розвиток теорії і експерименту показало, що змінні в часі електричні і магнітні поля можуть існувати обо-собления, незалежно від порушили їх зарядів, і поширюються в просторі у вигляді електромагнітних хвиль, спо-собнимі переносити енергію. Це переконай-кові підтверджує основне положення теорії близкодействия про локалізацію енергії в поле і що носієм енергії є поле.
Два рівних за величиною заряду протилежного знаку, + Q и- Q, розташованих на відстані l один від одного, утворюють електричний диполь. Величина Ql називається дипольним моментом і позначається символом р. Дипольниммоментом мають багато молекули, напри-заходів двухатомная молекула СО (атом С має невеликий позитивний заряд, а О - невеликий негативний заряд); незважаючи на те що молекула в цілому нейтральна, в ній відбувається поділ зарядів через нерівного розподілу електронів між двома атомами. (Сім-метричних двоатомних молекули, такі, як О2. Не володіють дипольним моментом.)
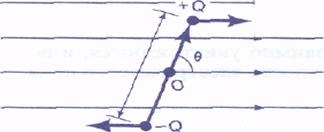
Розглянемо спочатку диполь з моментом # 961; = Ql, поміщений в однорідне електричне поле напруженістю # 917 ;. Дипольний момент можна пред-ставити у вигляді вектора р, рівного за абсолютною величи-ні Ql і спрямованого від негативного заряду до поло-тивних. Якщо поле однорідне, то сили, що діють на позитивний заряд, QE, і негативний, - QE, не створюють результуючої сили, що діє на диполь. Однак вони призводять до виникнення крутного мо-мента, величина якого щодо середини диполя Про дорівнює
або у векторній запису
В результаті диполь прагне повернутися так, щоб вектор p був паралельний Е. Робота W, здійснюється електричним полем над диполем, коли кут # 952; вимірюв-вується від q1 до q2. дається виразом
В результаті роботи, яку здійснюють електричним полем, зменшується потенційна енергія U диполя; якщо по-ложить U = 0, коли p ^ # 917; (# 952; = 90 0), то
U = -W = - pEcos # 952; = - p · # 917 ;.
Якщо електричне поле неоднорідне, то сили, що діють-щие на позитивний і негативний заряди диполя, можуть виявитися неоднаковими за величиною, і тоді на диполь, крім обертального моменту, буде діяти ще й результуюча сила.
Отже, ми бачимо, що відбувається з електричним диполем, поміщеним у зовнішнє електричне поле. Звернемося тепер до іншої сторони справи.
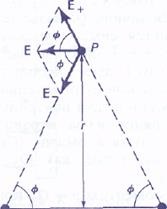
Мал. Електричне по-ле, створюване електричним диполем.
Припустимо, що зовнішнє поле відсутнє, і визначимо електричне поле, створюване самим диполем (здатне діяти на інші заряди). Для простоти обмежимося точками, розташованими на перпендикуляр до середини диполя, подібно точці # 929; на рис. що знаходиться на расстоя-ванні rот середини диполя. (Зауважимо, що rна рис. Не є відстанню від кожного із зарядів до Р, кото-рої одно (r 2 + / 2/4) 1/2) .напружених електричного поля в: точці # 929; дорівнює
де Е + та Е - напруженість поля, створювані відповід-повідно позитивним і негативним зарядами, рівні між собою за абсолютною величиною:
Їх y-компоненти в точці # 929; взаємно знищуються, і по абсолютній величині напруженість електричного поля # 917; дорівнює
[Уздовж перпендикуляра до середини диполя].
Далеко від диполя (r »/) це вираз спрощується:
[Уздовж перпендикуляра до середини диполя, при r >> l].
Видно, що напруженість електричного поля диполя зменшується з відстанню швидше, ніж для точкового заряду (як 1 / r 3 замість 1 / r 2). Цього і слід було очікувати: на великих відстанях два заряду протилежних знаків здаються настільки близькими, що нейтралізують один одного. Залежність виду 1 / r 3 справедлива і для точок, які не лежать на перпендикуляр до середини диполя.