Ентропія алфавіту - це кількість інформації, що припадає на один символ. Символи равновероятного алфавіту несуть максимальне інформаційне навантаження
Алфавіти природних мов не є рівноімовірними. Наприклад, відносна частота появи окремих символів російської мови змінюється від 0,175 до 0,002.
Внаслідок статистичних властивостей алфавіту інформаційне навантаження на один символ знижена на
Надмірністю алфавіту називається зменшення інформаційного навантаження на один символ внаслідок неравновероятності і взаємозалежності появи його символів.
Інформаційна надмірність, що характеризує відносну недовантаження алфавіту розраховується так:
Рівномірні коди характеризуються мінімальної розрядністю кодових слів, яка розраховується за формулою
де N - обсяг вихідного алфавіту А;
M - обсяг кодового алфавіту В;
[LogM N] означає цілу частину числа logM N
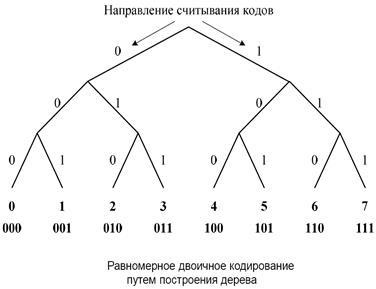
Розглянемо ці формули для випадку двійкового кодування (т. Е. При М = 2). Мінімальна розрядність рівномірного коду для алфавіту об'ємом 8 символів буде дорівнює
rmin = log2 8 = 3 довічних символу
А для 9-літерного алфавіту
Нерівномірні коди характеризуються середньою довжиною кодового слова
li - довжина кодового слова i -го символу;
pi - ймовірність появи i-го символу;
N - обсяг вихідного алфавіту.
Наприклад, якщо алфавіт А = a, b, c, d, e> з ймовірності появи символів в повідомленні (pa = 0,5; pb = 0,2; pc = 0,1; pd = 0,15; pe = 0 , 05) закодований двійковим нерівномірним кодом (a - 0; b - 10; c - 1110; d - 110; e - 1111), то середня довжина кодового слова для такого алфавіту буде
Таким чином, середня довжина кодового слова є сума довжин всіх кодових слів, узятих з вагою, рівним ймовірності появи кодованого символу.
Кількість і обсяг інформації


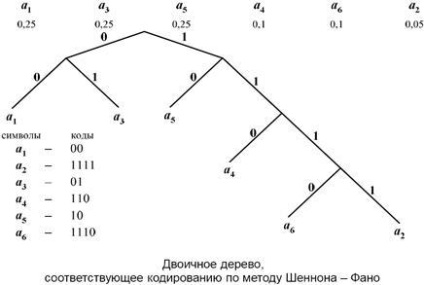
Метод Шеннона - Фано
Крок 1. Упорядковуємо символи вихідного алфавіту в порядку незростання їх ймовірностей. (Записуємо їх в рядок).
Крок 2. Не змінюючи порядку символів, ділимо їх на дві групи так, щоб сумарні ймовірності символів в групах були по можливості рівні.
Крок 3. приписують групі зліва "0", а групі справа "1" в якості елементів їх кодів.
Крок 4. Переглядаємо групи. Якщо число елементів в групі більше одного, йдемо на Крок 2. Якщо в групі один елемент, побудова коду для нього завершено.
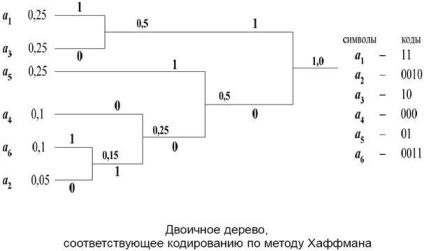
Крок 1. Упорядковуємо символи вихідного алфавіту в порядку незростання їх ймовірностей. (Записуємо їх в стовпець).
Крок 2. Об'єднуємо два символу з найменшими ймовірностями. Символ з більшою ймовірністю приписуємо "1", символу з меншою - "0" як елементи їх кодів.
Крок 3. Вважаємо об'єднання символів за один символ з імовірністю, яка дорівнює сумі ймовірностей об'єднаних символів.
Крок 4. Повертаємося на крок 2 до тих пір, поки всі символи НЕ будуть об'єднані в один з ймовірністю, яка дорівнює одиниці.