ФІГУРНІ ЧИСЛА
Про числа 25, 49, 100 кажуть, що вони є квадратами. А чому? Тому що вони виходять, якщо звести числа 5, 7 і 10 в квадрат. Але чи має це назва якесь відношення до геометричної фігури - квадрату? Подивимося на рис. 1. Солдати стоять правильними рядами, утворюючи квадрати. Число солдатів всередині такого квадрата легко підрахувати - потрібно помножити їх число уздовж горизонтальної сторони на число солдатів уздовж вертикальної сторони (зауважимо, що ці числа рівні), і вийде загальна кількість солдатів всередині квадрата.

У давнину обчислювачі часто вважали за допомогою камінчиків і, природно, спостерігалися випадки, коли камінці можна було скласти у вигляді правильної фігури. Крім квадратних чисел були відомі трикутні числа, які виходять так, як це показано на рис. 2 у верхній його частині. Неважко помітити, що -е квадратне число одно, а -е трикутне число дорівнює сумі всіх цілих чисел від 1 до, тобто (Див. Арифметична прогресія).
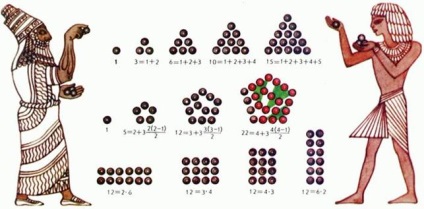
П'ятикутні числа зображені на рис. 2. Щоб порахувати -е п'ятикутне число, його потрібно розбити на три трикутних, після чого залишиться ще точок, як показано на малюнку. В результаті отримуємо, що -е п'ятикутне число одно.
Подібним чином можна утворювати будь-які багатокутні числа. Формула для -го -угольного числа така:
При ми отримуємо трикутні числа, при - квадратні і т.д.
Аналогічно можна уявити число у вигляді прямокутника. Для числа 12 це можна зробити багатьма способами (рис. 2), а для числа 13 - лише розташувавши всі предмети в одну лінію. Таке число давні не вважали прямокутним. Таким чином, прямокутними числами є всі складові числа, а непрямокутних - прості числа.
До фігурним числам також відносяться пірамідальні числа, які виходять, якщо кульки складати пірамідою, як раніше складали ядра близько гармати. Неважко помітити, що -е пірамідальне число дорівнює сумі всіх трикутних чисел - від першого до -го. Формула для обчислення -го пірамідального числа має вигляд