Формули коренів квадратного рівняння
Нехай дано квадратне рівняння ах 2 + b х + с = 0.
Застосуємо до квадратному тричленну ах 2 + b х + с ті ж перетворення, які ми виконували в § 13, коли доводили теорему про те, що графіком функції у = ах 2 + b х + с є парабола.
маємо
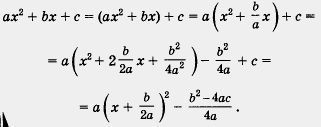
Зазвичай вираз b 2 - 4ас позначають буквою D і називають дискримінантом квадратного рівняння ах 2 + b х + с = 0 (або дискримінантом квадратного тричлена ах + b х + с).
Значить, квадратне рівняння ах 2 + їх + з = О можна переписати у вигляді
Будь-яке квадратне рівняння можна перетворити до вигляду (1), зручному, як ми зараз переконаємося, для того, щоб визначати число коренів квадратного рівняння і знаходити ці коріння.
Доведення. якщо D <0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.
Приклад 1. Вирішити рівняння 2x 2 + 4х + 7 = 0.
Рішення. Тут а = 2, b = 4, с = 7,
D = b 2 -4ac = 4 2. 4. 2. 7 = 16-56 = -40.
Так як D <0, то по теореме 1 данное квадратное уравнение не имеет корней.
Доведення. Якщо D = 0, то рівняння (1) приймає вигляд
- єдиний корінь рівняння.
Зауваження 1. Чи пам'ятаєте ви, що х = - - абсциса вершини параболи, яка служить графіком функції у = ах 2 + їх + с? Чому саме це
значення виявилося єдиним коренем квадратного рівняння ах 2 + їх + с - 0? «Скринька» відкривається просто: якщо D - 0, то, як ми встановили раніше,
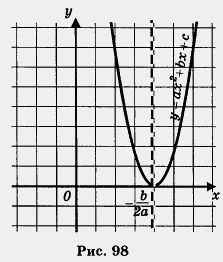
Графіком ж функції є парабола з вершиною в точці (див. Наприклад, рис. 98). Значить, абсциса вершини параболи і єдиний корінь квадратного рівняння при D = 0 - одне і те ж число.
Приклад 2. Вирішити рівняння 4x 2 - 20x + 25 = 0.
Рішення. Тут а = 4, b = -20, з = 25, D = b 2 - 4ас = (-20) 2 - 4 • 4 • 25 = 400 - 400 = 0.
Так як D = 0, то по теоремі 2 дане квадратне рівняння має один корінь. Цей корінь знаходиться за формулою
Зауваження 2. Зверніть увагу, що 4х 2 - 20х +25 - повний квадрат: 4х 2 - 20х + 25 = (2х - 5) 2.
Якби ми це помітили відразу, то вирішили б рівняння так: (2х - 5) 2 = 0, значить, 2х - 5 = 0, звідки отримуємо х = 2,5. Взагалі, якщо D = 0, то
ах 2 + b х + с = - це ми відзначили раніше в зауваженні 1.
Якщо D> 0, то квадратне рівняння ах 2 + b х + с = 0 має два корені, які знаходяться за формулами
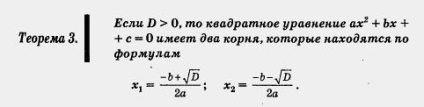
Доведення. Перепишемо квадратне рівняння ах 2 + Ь х + с = 0 у вигляді (1)
покладемо
За умовою, D> 0, значить, права частина рівняння позитивне число. Тоді з рівняння (2) отримуємо, що

Отже, заданий квадратне рівняння має два кореня:
Зауваження 3. У математиці досить рідко буває так, щоб введений термін не мав, образно висловлюючись, життєвої підгрунтя. візьмемо нове
поняття - дискримінант. Згадайте слово «дискримінація». Що воно значить? Воно означає приниження одних і піднесення інших, тобто різне ставлення-
ня до різних пюдям. Обидва слова (і дискримінант, і дискримінація) походять від латинського discriminans - «розрізняє». Дискримінант розрізняє квадратні рівняння за кількістю коренів.
Приклад 3. Розв'язати рівняння Зх 2 + 8х - 11 = 0.
Рішення. Тут а = 3, b = 8, с = - 11,
D = b 2 - 4ас = 8 2 - 4 • 3 • (-11) = 64 + 132 = 196.
Так як D> 0, то по теоремі 3 дане квадратне рівняння має два кореня. Ці корені знаходяться за формулами (3)
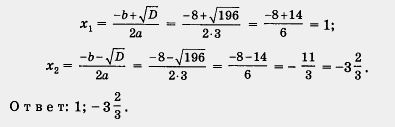
Фактично ми з вами виробили наступне правило:
Правило рішення рівняння
ах 2 + b х + с = 0

Це правило універсально, воно може бути застосовано як до повних, так і до неповним квадратним рівнянням. Однак неповні квадратні рівняння зазвичай за цим правилом не вирішують, їх зручніше вирішувати так, як ми це робили в попередньому параграфі.
Приклад 4. Вирішити рівняння:
а) х 2 + Зх - 5 = 0; б) - 9x 2 + 6х - 1 = 0; в) 2х 2-х + 3,5 = 0.
Р і ш е н і е. А) Тут а = 1, b = 3, с = - 5,
D = b 2 - 4ас = З 2 - 4 • 1 • (- 5) = 9 + 20 = 29.
Так як D> 0, то дане квадратне рівняння має два кореня. Ці корені знаходимо за формулами (3)
б) Як показує досвід, зручніше мати справу з квадратними рівняннями, у яких старший коефіцієнт позитивний. Тому спочатку помножимо обидві частини рівняння на -1, отримаємо
9x 2 - 6x + 1 = 0.
Тут а = 9, b = -6, з = 1, D = b 2 - 4ас = 36 - 36 = 0.
Так як D = 0, то дане квадратне рівняння має один корінь. Цей корінь знаходиться за формулою х = -. значить,
Це рівняння можна було вирішити по-іншому: так як
9х 2 - 6x + 1 = (Зх - IJ, то отримуємо рівняння (Зх - I) 2 = 0, звідки знаходимо Зх - 1 = 0, т. Е. Х =.
в) Тут а = 2, b = - 1, з = 3,5, D = b 2 - 4ас = 1 - 4 • 2 • 3,5 = 1 - 28 = - 27. Так як D <0, то данное квадратное уравнение не имеет корней.
Математики - люди практичні, економні. Навіщо, кажуть вони, користуватися таким довгим правилом рішення квадратного рівняння, краще відразу написати загальну формулу:
Якщо виявиться, що дискримінант D = b 2 - 4ас - негативне число, то записана формула не має сенсу (під знаком квадратного кореня знаходиться негативне число), значить, коріння немає. Якщо ж виявиться, що дискримінант дорівнює нулю, то отримуємо
т. е. один корінь (кажуть також, що квадратне рівняння в цьому випадку має два однакових кореня:
Нарешті, якщо виявиться, що b 2 - 4ас> 0, то виходять два кореня х1 і х2. які обчислюються за тими ж формулами (3), що вказані вище.
Саме число в цьому випадку позитивно (як всякий квадратний корінь з позитивного числа), а подвійний знак перед ним означає, що в одному випадку (при знаходженні х1) це позитивне число додається до числа - b, а в іншому випадку (при знаходженні х2) це позитивне число ви-
читається з числа - b.
У вас є свобода вибору. Хочете - вирішуйте квадратне рівняння докладно, використовуючи сформульоване вище правило; хочете - запишіть відразу формулу (4) і з її допомогою робіть необхідні висновки.
Приклад 5. Вирішити рівняння:
Рішення, а) Звичайно, можна використовувати формули (4) або (3), з огляду на, що в даному випадку Але навіщо виконувати дії з дробами, коли простіше і, головне, приємніше мати справу з цілими числами? Давайте звільнимося від знаменників. Для цього потрібно помножити обидві частини рівняння на 12, т. Е. На найменший спільний знаменник дробів, службовців коефіцієнтами рівняння. отримаємо
звідки 8х 2 + 10x - 7 = 0.
А тепер скористаємося формулою (4)
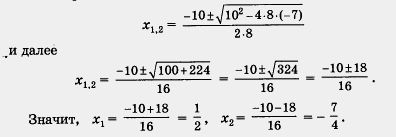
б) Ми знову маємо рівняння з дробовими коефіцієнтами: а = 3, b = - 0,2, з = 2,77. Помножимо обидві частини рівняння на 100, тоді отримаємо рівняння з цілими коефіцієнтами:
300x 2 - 20x + 277 = 0.
Далі скористаємося формулою (4):
Проста прикидка показує, що дискримінант (подкоренное вираз) - негативне число. Значить, рівняння не має коренів.
Приклад 6. Розв'язати рівняння
Рішення. Тут, на відміну від попереднього прикладу, краще діяти за правилом, а не за скороченою формулою (4).
Маємо а = 5, b = -. з = 1, D = b 2 - 4ас = (-) 2 - 4 • 5 • 1 = 60 - 20 = 40. Так як D> 0, то квадратне рівняння має два кореня, які будемо шукати за формулами (3)
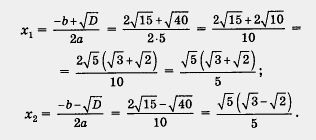
Приклад 7. Розв'язати рівняння
х 2 - (2р + 1) x + (р 2 + р-2) = 0
Рішення. Це квадратне рівняння відрізняється від усіх розглянутих досі квадратних рівнянь тим, що в ролі коефіцієнтів виступають не конкретні числа, а літерні вирази. Такі рівняння називають рівняннями з літерними коефіцієнтами або рівняннями з параметрами. В даному випадку параметр (буква) р входить до складу другого коефіцієнта і вільного члена рівняння.
Знайдемо дискримінант:
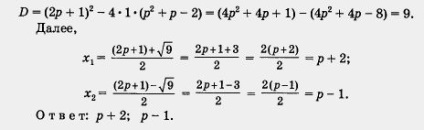
Приклад 8. Розв'язати рівняння рx 2 + (1 - р) х - 1 = 0.
Рішення. Це також рівняння з параметром р, але, на відміну від попереднього прикладу, його не можна відразу вирішувати за формулами (4) або (3). Справа в тому, що зазначені формули застосовні до квадратних рівнянь, а про задане рівняння ми цього поки сказати не можемо. Справді, а раптом р = 0? тоді
рівняння набуде вигляду 0 • x 2 + (1-0) x- 1 = 0, т. е. х - 1 = 0, звідки отримуємо х = 1. Ось якщо точно відомо, що. то можна застосовувати формули коренів квадратного рівняння: