При великих значеннях n використання формули Бернуллі пов'язане з трудомісткими обчисленнями. Нехай нам потрібно обчислити:
Ясно, що це технічно складно. У подібних випадках використовують формулу, яка є граничним випадком формули Бернуллі.
Локальна формула Лапласа. Якщо ймовірність p появи події A постійна в кожному випробуванні і відмінна від 0 і 1, то ймовірність того, що подія A настане k раз в n незалежних випробуваннях, при досить великому числі n приблизно дорівнює
де - функція Гаусса (рисунок 2.2),.
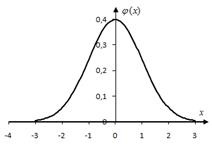
Чим більше n. тим точніше формула (2.3). При вона дає задовільні для практики результати.
Значення функції Гаусса наведені в таблиці Б.1 додатка Б.
Властивості функції Гаусса:
1. - парна функція, тобто .
2. функція монотонно убуває при позитивних значеннях x. причому при (практично можна вважати, що вже при).
Приклад 2.3. Імовірність виготовлення деталі вищого гатунку на даному верстаті дорівнює 0,4. Знайти ймовірність того, що серед навмання взятих 56 деталей половина виявиться вищого гатунку.
Рішення. n велике,. тому застосуємо локальну формулу Лапласа (2.3). Проведемо необхідні обчислення:
Наступна формула Лапласа дозволяє знаходити ймовірність того, що подія A в n незалежних випробуваннях настане не менше і не більше разів.
Інтегральна формула Лапласа. Якщо ймовірність p настання події A в кожному випробуванні постійна і відмінна від 0 і 1, то ймовірність того, що подія A в n незалежних випробуваннях настане не менше і не більше разів, при досить великому числі n приблизно дорівнює
- функція Лапласа, (2.5)
При формула (2.4) дає, як правило, задовільну для практики похибка обчислення ймовірності.
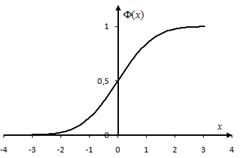
Значення функції можна знайти в таблиці Б.2 додатків. Графік зображений на малюнку 2.3. Перерахуємо властивості функції Лапласа.
1.Функция непарна, т. Е..
2.Функция монотонно зростає, при (практично можна вважати, що вже при).
Приклад 2.4. В деякій місцевості з кожних 100 сімей 80 мають холодильник. Яка ймовірність, що від 300 до 360 сімей включно з 400 обстежених мають холодильники?
Добре б приклад технічний
Рішення. Застосуємо інтегральну формулу Лапласа (. Спочатку визначимо за формулами (2.6)
Далі за формулою (2.4), враховуючи властивості функції # 934; (x), отримаємо:
(З таблиці Б.2 додатка Б:).
Розглянемо наслідок інтегральної формули Лапласа.
Слідство. Якщо ймовірність p настання події A в кожному випробуванні постійна і відмінна від 0 і 1, то при досить великому числі незалежних випробувань ймовірність наступних подій визначаються за формулами:
а) відносна частота події A укладена в межах від a до b:
б) відносна частота події A відрізняється від його ймовірності не більше, ніж на величину (по абсолютній величині):
При і формули Лапласа дають задовільну для практики похибка обчислення ймовірності. Якщо n одного порядку з 1 / n при великих n, або. більш точний результат дає формула Пуассона
2.1. Скільки потрібно взяти деталей, щоб найімовірніше число придатних деталей дорівнювало 50, якщо ймовірність того, що навмання взята деталь буде бракованою, дорівнює 0,1?