Нерухомим називають блок. вісь якого є закріпленої і не переміщається при підйомі вантажів. Умови рівноваги блоку визначають з умови рівноваги моментів сил, які до нього додаються.
Блок на рис.1 буде перебувати в рівновазі, якщо сили, так як плечі цих сил однакові (ОА = ОВ). Блок - це важіль, який має такі самі плечі. Блок, який представлений на рис.1 не дає виграшу в силі, проте він дозволяє змінювати напрямок дії сили. Тягнути за мотузку, яка йде зверху зазвичай зручніше, ніж за мотузку, яка йде знизу.
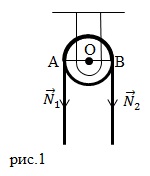
Припустимо, що через блок, який є суцільним диском радіусом R і масою m, перекинута нерозтяжна нитка, яка нездатна ковзати по блоку. На нитки повісили вантажі масами і (рис.2). Визначимо, які прискорення вантажів (і) і різницю натягу ниток.
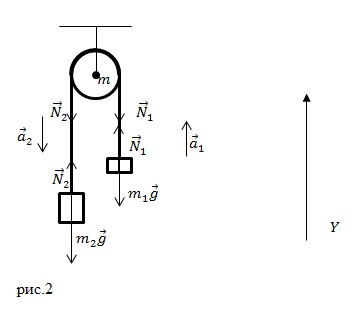
Рівняння рух вантажу номер один буде мати вигляд:
У проекції на вісь Y, отримаємо:
Для другого вантажу відразу напишемо рівняння руху в проекції на вісь Y \ ^
Так як ми вважаємо нитка нерастяжимой, то прискорення першого і другого вантажів однакові по модулю:
Врахуємо рівність (4), складемо рівняння (2) і (3), отримаємо:
Далі необхідно розглянути рівняння обертального руху блоку. Моменти сил, які створюються силами натягу нитки, мають протилежні знаки, тому запишемо:
де J - момент інерції блоку; - кутове прискорення блоку. Вираз (6) перетворимо до виду:
З формул (5) і (7) маємо:
Якщо можна в завданні масу блоку не враховувати (момент інерції блоку малий), то можна вважати, що виконується умова:
то різниця натяжений ниток істотно менше різниць сили тяжіння вантажів. Для невагомого блоку матимемо такі формули:
Приклади розв'язання задач за темою «Нерухомий блок»
Через блок, який має масу кг, перекинута нерозтяжна нитку. До кінців нитки прив'язані вантажі, що мають маси кг і кг. З яким прискоренням (a) будуть переміщатися вантажі, якщо блок вважати суцільним диском?
Так як нитка нерастяжима, то вантажі будуть рухатися з рівними по величині ускорениями, але протилежно спрямованими. Так як за умовою завдання блок має масу, для вирішення задачі використовуємо формулу:
Момент інерції (J) суцільного диска щодо осі, що проходить через його центр мас дорівнює:
Підставами вираз (1.2) в формулу (1.1), маємо:
Обчислимо прискорення вантажів:
Машину Атвуда використовують для розгляду законів рівноприскореного руху тел. Вона являє собою два вантажу з різними масами, які підвішені на майже невагомою нитки, яка перекинута через нерухомий блок. Чому рівні сили натягу нитки, якщо блок вважати невагомим? Маси вантажів рівні і).
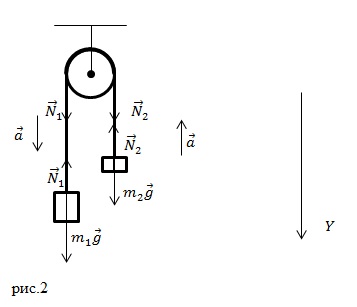
Якщо блок вважаю невагомим, то:
При цьому прискорення вантажів одно: