Аналогічно, множачи рівність (3.49) на і інтегруючи в межах від до, отримуємо:
,
Таким чином, коефіцієнти і ряду (3.49) визначаються єдиним чином формулами (3.50) - (3.52), що і доводить теорему.
Ця теорема дає підставу ввести таке визначення.
Визначення. Функціональний ряд виду:
де коефіцієнти визначаються за формулами:
називається поруч Фурьефункцііf (x). Відзначимо, що завжди.
З'ясуємо, якими властивостями повинна володіти функція f (x), щоб побудований для неї ряд Фур'є сходився, і щоб сума побудованого ряду Фур'є дорівнювала значенням даної функції у відповідних точках.
Визначення. Функція f (x) називається кусочно-монотонної на відрізку [a. b], якщо відрізок можна розбити кінцевим числом точок на інтервали так, щоб в кожному з них функція була монотонна.
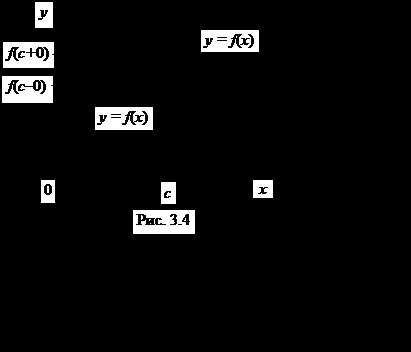
З визначення випливає, що якщо функція f (x) - кусочно-монотонна і обмежена на відрізку [a. b], то вона може мати тільки точки розриву першого роду. Дійсно, якщо є точка розриву функції f (x), то в силу монотонності функції існують межі:
тобто точка є точка розриву першого роду (рис. 3.4).
Теорема 3.7. Якщо функція f (x) періодична з періодом, кусочно-монотонна і обмежена на відрізку, то
для будь-якої точки безперервності (тобто є сумою свого ряду Фур'є). Якщо ж точка - точка розриву першого роду функції, то сума ряду Фур'є в цій точці
,
де - межі ліворуч і праворуч відповідно в точці х.
З теореми випливає, що в точках безперервності функції і сума дорівнює середньому арифметичному меж ліворуч і праворуч функції в точках розриву першого роду.
З теореми випливає також, що клас функцій, які представлені рядами Фур'є, досить широкий. Тому ряди Фур'є знайшли широке застосування в різних розділах математики. Особливо успішно ряди Фур'є застосовуються в математичній фізиці і її додатках до конкретних завдань механіки і фізики.
Приклад 1. Розкласти в ряд Фур'є функцію, що має період і задану на проміжку наступним чином: