
Робота з цифрами 6 і 12 знайомить нас з шестикутниками. гексаграммами. додекагонамі (дванадцять сторонніх полігонів) і поруч додекаграмм. але також включає в себе трикутники як само собою зрозуміле.
Перша операція, на яку ми дивимося, ймовірно, найстаріша геометрична конструкція, відома людству, тому що вона вимагає лише циркуля або його древнього еквіваленту - мотузки. Я пам'ятаю, як випадково виявив це в дитинстві, граючи мляво з циркулем, і випробував дивовижний захват, який, я впевнений, у багатьох був.
Розподіл кола на 6
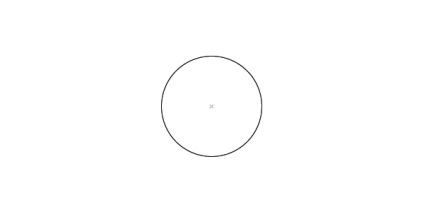
Утримуючи одне і те ж отвір циркуля, помістіть чорнову точку вгорі або внизу кола і намалюйте інший гурт.
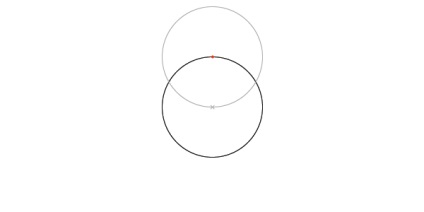
Перемістіть чорнову точку в будь-яку з точок перетину, щойно створену, і намалюйте інший гурт.
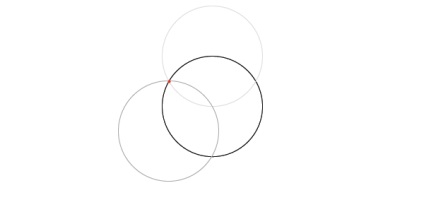
Таким чином обійдіть весь круг. Шостий коло проходить через вершину першого (чорного) кола, і тому завершує малюнок. Коло тепер розділений на 6.
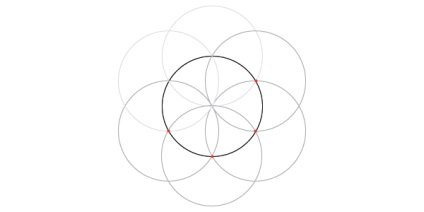
Розподіл кола на 12
Почніть з описаних вище кроків, щоб розділити його на 6. Потім підключіть найвіддаленіші точки перетину, як показано тут. Ці лінії обрізають коло ще в шести точках, так що тепер він ділиться на 12.
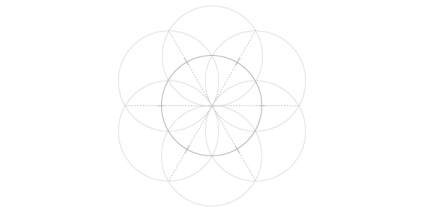
Шестикутник і гексаграмма
Вони створюються по колу, розділеному на шість, шляхом об'єднання шести точок, позначених на колі. Якщо ми починаємо розподіл зверху чи знизу першого кола, як ми тут робили, форми є динамічними.
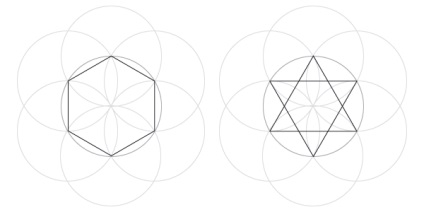
Щоб зробити їх статичними, або починайте розподіл ліворуч або праворуч від кола, або продовжуйте до тих пір, поки воно не розділиться на 12, а замість цього вставте набір з шести точок.
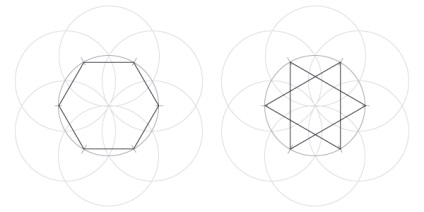
Зверніть увагу, як гексаграмма утворена двома рівносторонніми трикутниками, а також меншим шестикутником і шістьма маленькими трикутниками.

Плитка з Єгипту або Сирії, XV століття.
Просто з'єднайте дванадцять точок на колі.
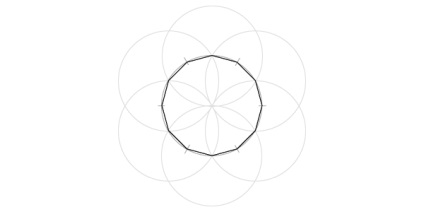
Альтернативний варіант
Іншим способом поділу кола в дванадцять є той, який ми вже вивчили на уроці по роботі з 4 і 8: виконайте кроки для малювання статичного квадрата і припиніть малювати сам квадрат. З'єднайте точки на колі, і ви виявите ідеальний додекагон.
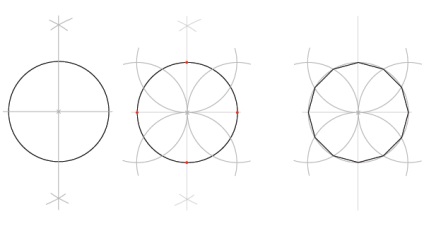
Як це можливо? Це проблиск магії чисел. 12 кратно 4, а також 6 або 3, і, отже, воно «пов'язане» з квадратними конструкціями, а також з трикутними. Додекагон - це місце, де можуть зустрічатися шестикутник і квадрат. Це проявляється навіть у таких формах:
Додекаграмми
Створюються чотири різні двенадцатіконечние зірки, в залежності від того, з'єднуємо ми кожну другу, третю, четверту чи п'яту точки, і вони відповідно утворені з шестикутників, квадратів, трикутників і, нарешті, однією суцільної лінії.
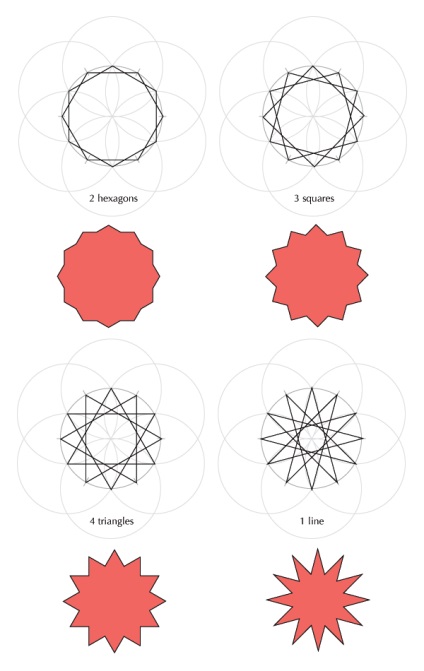
Ще одна гексаграма
Остання додекаграмма може служити сіткою для малювання інший шестикутної зірки, статичної або динамічної, в залежності від того, які точки опущені.
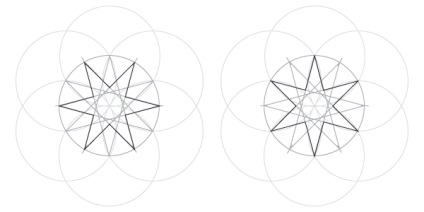
семигранну сітка
Раніше ми вчилися малювати сітку з п'яти кіл, яка генерує сітку з квадратів. Для 6 і 12 ми побудуємо сітку з семи кіл. щоб створити три кореневих (√3) шаблону.
Дотримуйтесь інструкцій, щоб розділити коло на шість.
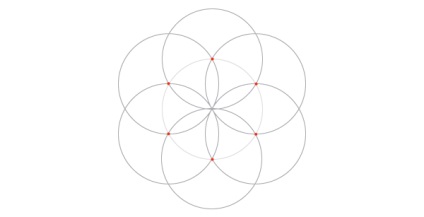
Намалюйте ще шість кіл, зосереджених по найбільш віддаленим точкам перетину. Відкриття циркуля ніколи не змінюється під час будівництва.
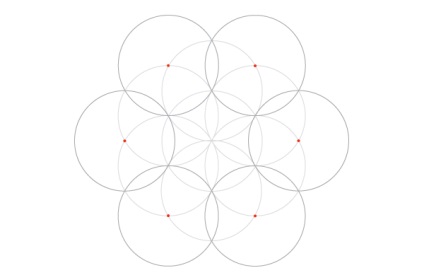
Повторіть на нових пересічних ще шість кіл. Ці кола, а також вихідний, який вони оточують, є сім кіл сітки, але нам потрібно заповнити «квітка» всередині кожної з них, щоб сітка була повністю функціональною.
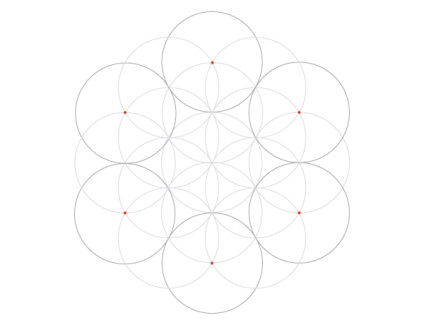
Знову помістіть чорнову точку на кожну нову, найдальшу точку перетину (тепер 12), але тільки намалюйте дугу, яка знаходиться всередині раніше намальованих кіл.
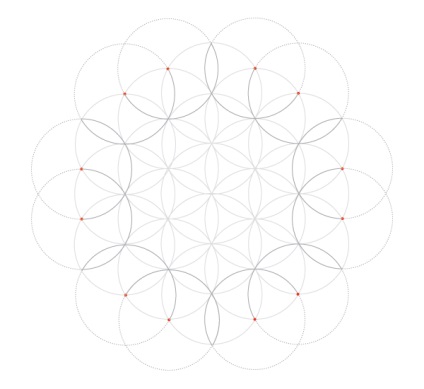
Закінчите з останніми відсутніми дугами.
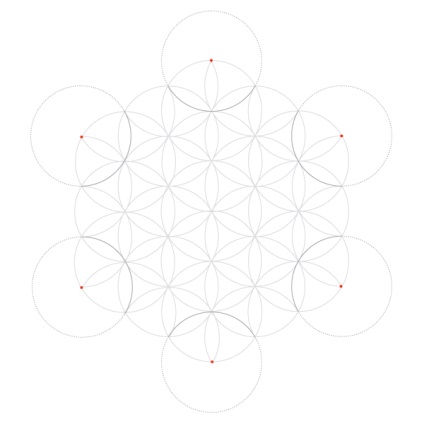
Ось готова сітка з виділеними сімома колами.
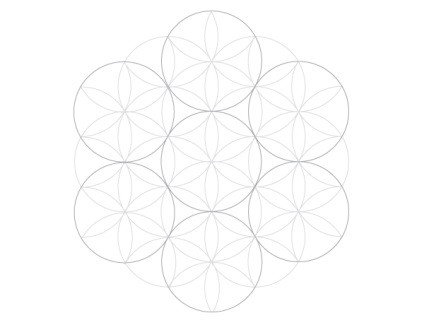
Без додавання чого-небудь ще, сама сітка надає безліч простих шаблонів. Просто виділіть кілька ліній (або колір в областях), щоб створити повторювані фігури. Для розширення шаблону можна додати нижні кола до нескінченності.
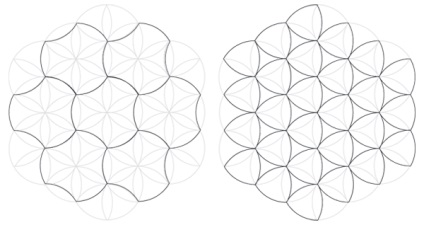
Сітка гексаграмм
Малювання гексаграми в кожному з кіл створює похідну сітку, яка однаково універсальна. Гексаграми не потрібно малювати одну за одною - вони з'являються, коли додаються деякі загальні лінії.
Почніть з одного набору діагоналей. Щоб уникнути плутанини, пам'ятайте, що вони проходять через верх або низ семи кіл (ігнорують проміжні кола).
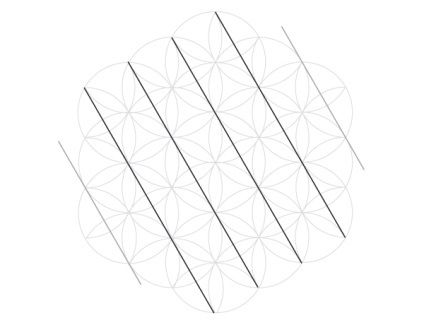
Тепер наступний набір, та ж ідея.

Нарешті, горизонталі, які доповнюють гексаграми. Зверніть увагу, що вони не проходять через центр жодного з семи головних кіл.
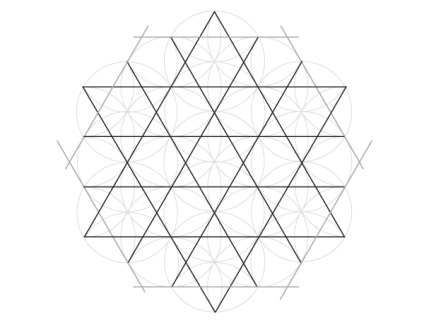
Ось закінчена сітка, що складається з шестикутників і трикутників.
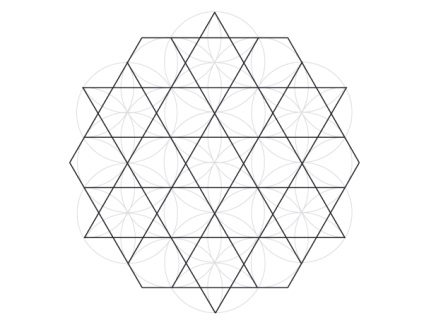
Вибіркова розфарбування створює всілякі шаблони, в тому числі такі незвичайні, як третій нижче. Сітка може бути необмежено розширена для розширення шаблону.


Занадто кострубатий? Ось як зробити цю сітку / візерунок пишною!
Вигнутий малюнок гексаграмм
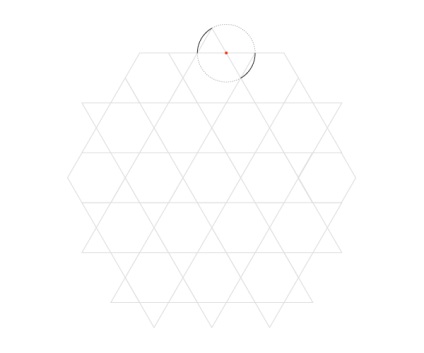
Повторіть з точкою, що відбиває перше.
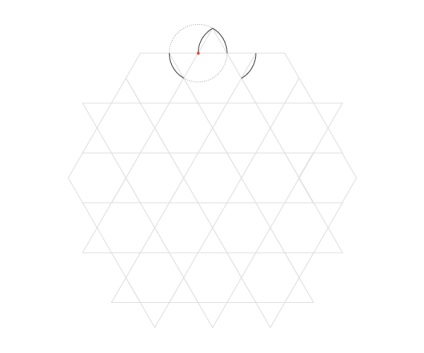
Продовжуйте рух навколо гексаграми.
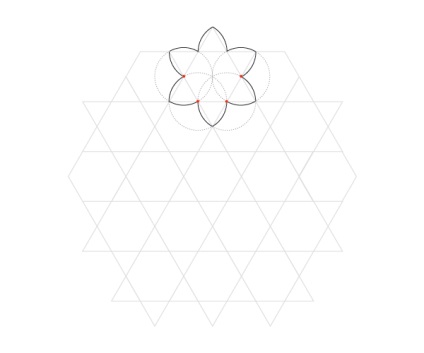
Повторіть з кожної гексаграми в сітці.
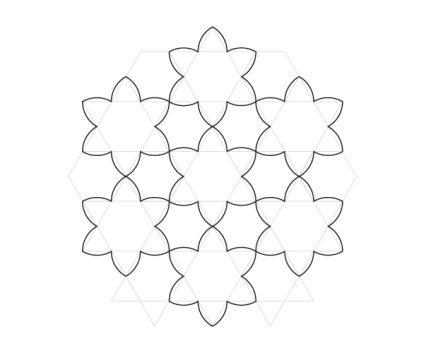

Сітка рівносторонніх трикутників
Це додатковий крок для подальшого розриву сітки, що створює ще більшу гнучкість в шаблонах. Почніть з сітки гексаграмм:

Додати один набір діагоналей.


Готово з відсутніми горизонталями.

Ось готова сітка.

Така базова сітка пропонує нескінченні можливості. Це як малювання пікселів, але з трикутними пікселями. На цьому заснована популярна гра-головоломка Tangram. Нижче наведено два приклади з сіткою, яка б показала і без неї (що значно послаблює присутність трикутників).
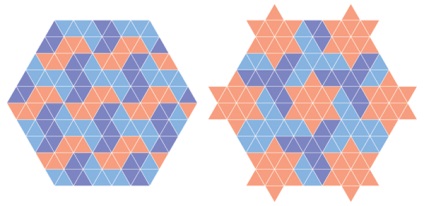
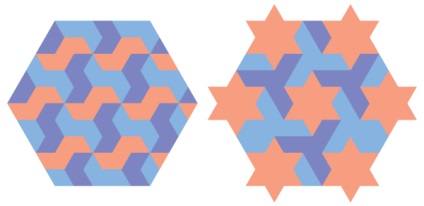
зразок додекаграмми
Ось інше використання сітки з семи кіл. Замість того, щоб ділити поверхню на плитки для індивідуального заповнення, ми збираємося будувати більш складні форми.
Наша відправна точка - це сітка гексаграмм:

Прокресліть або принаймні затемніть зовнішній контур кожної гексаграми, так як це остаточні лінії. Деталі в семи колах можуть бути стерті для ясності, але нам потрібні їх контури.

Нам потрібно розділити кожен коло на 12. Щоб зробити це навалом, додайте діагоналі, як би ладу сітку з трикутників, спочатку в одну сторону.


і, нарешті, горизонталі.

Працюючи в виділеному колі, з'єднайте шість нових точок, щоб сформувати другу гексаграми.

Тепер закресліть контур гексаграми.
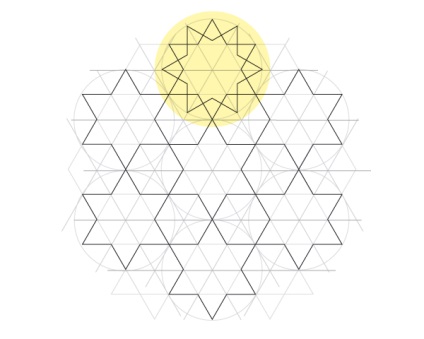
Повторіть кроки 3 і 4 в кожному колі. Цей остаточний проект може бути заповнений або пліток (як це зробити, буде розглянуто на наступному занятті).
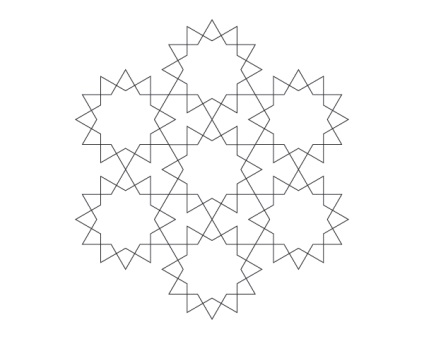
Зразок з квадратами, трикутниками і шестикутниками
Давайте закінчимо зі злегка хитрою, але по-іншому виглядає моделлю. В якості основи для цього потрібно сітка з семи кіл плюс повна трикутна сітка. Цей шаблон найкраще виглядає на розширеній сітці, де він може повторювати більше, але ми будемо дотримуватися семи кіл для демонстрації.
Ось наша початкова сітка, яка використовує різні кольори для кіл і трикутників, для ясності.
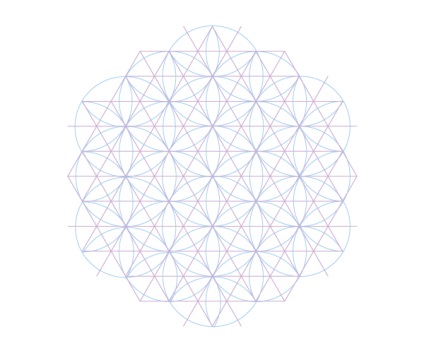
Почнемо з центрального кола. Знайдіть і відзначте перетину нижче. Вони складні, тому що вони не перетин прямих або кіл, а чотири точки на контурі цього центрального шестикутника, де він вирізається дугами.
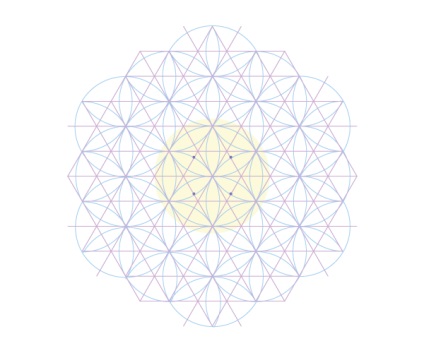
Якщо ви отримали правильні точки, приєднання до них дає ідеальний квадрат.
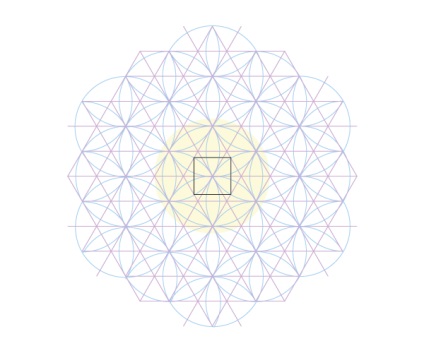
Все, що ми збираємося зробити для цього шаблону, - це малювати ці квадрати. Це досить складно, з цієї складної сіткою, і остання повинна бути намальована дуже акуратно.
Давайте тепер визначимо квадрати в верхньому і нижньому колах. Вони також є статичними, тому точки легко виявити.
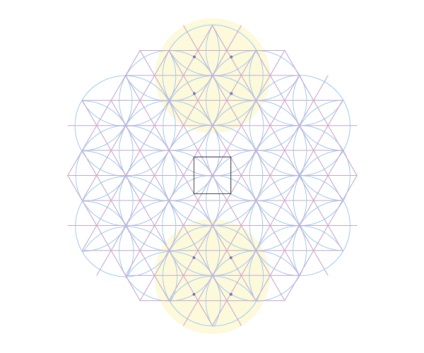
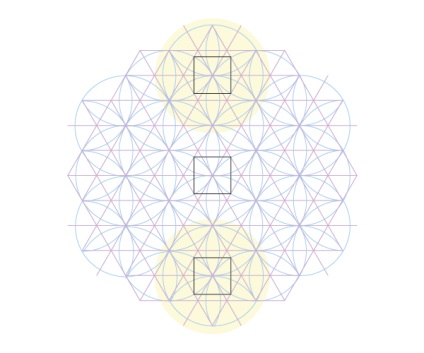
Ті ж самі квадрати можна знайти в останніх чотирьох з семи кіл, все статичні.
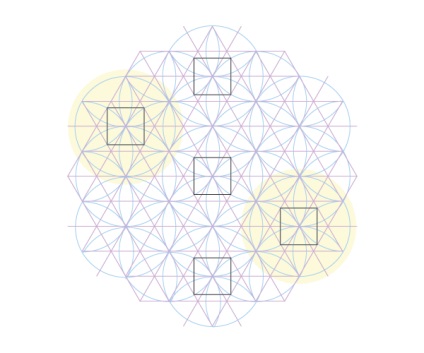
Тепер перейдемо до проміжних колам внизу, які виробляють похилі квадрати. Знаючи, що дві з чотирьох точок збігаються з кутами динамічних квадратів, ми можемо знайти дві інші точки для кожного з них. Перетину ті ж, що і раніше, але під кутом.
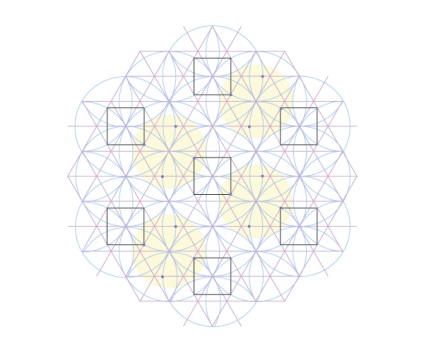
Поєднуючи точки, ось квадрати:
Тепер легко візуалізувати залишилися квадрати, коли ми звернемося до решти проміжним колах - в більш повному малюнку їх чотири кути будуть вже визначені, так як вони знаходяться в двох ближче до центру нижче.
Ось зразок без сітки (я додав чотири зовнішніх квадрата, щоб «закрити» його, так що це більш зрозуміло). Зверніть увагу, що коли три квадрата торкаються один одного, вони укладають в рівносторонній трикутник, і кожне коло з шести квадратів створює шестикутник. Звичайно, ви також можете добитися того ж результату, знайшовши замість нього шестикутники і / або трикутники.
Це всього лише частина шаблону, насправді: правильний спосіб зробити це - продовжити сітку кіл до краю поверхні, яку ви заповнюєте, намалювати рівномірно широку сітку трикутників, а потім знайти всі задіяні квадрати.
Тоді ви отримаєте наступне, і коли воно забарвлене, може різко змінити форми.
Це буде 6 і 12! Ми не тільки навчилися працювати з трикутниками, шестикутниками і додекагонамі (і суміжними зірками), ми також бачили, як їх об'єднати з квадратами, і як семікруговая сітка може давати не тільки різні візерунки, але і інші сітки.
В наступному місяці ми будемо працювати з останньою парою чисел, 5 і 10, а також з деякими непарними числами, такими як 7 і 9.