Для побудови гістограми потрібно визначити наступні параметри:
1. Граничні точки.
2. У нашому випадку граничними точками будуть значення 162 і 190 (мінімальне і максимальне значення у вибірці)
3. Кількість класів гістограми, визначається як корінь квадратний з обсягу вибірки.
У нашому випадку обсяг вибірки дорівнює шістнадцяти, тобто кількість класів: sqrt (16) = 4
4. Ширина одного класу: відстань між граничними точками потрібно розділити на кількість класів.
У нашому випадку ширина одного класу обчислюється як (190-162) / 4 = 7
Тепер потрібно визначити межі кожного класу:
1-й клас: 162-168
2-й клас: 169-175
3-й клас: 176-182
4-й клас: 183-190
Після того, як ми нанесли <сетку> гістограми на систему координат, потрібно відзначити кількість подій з нашої вибірки, що потрапляють в той чи інший клас.
На гістограмі видно, наскільки часто в нашій вибірці зустрічається те чи інше значення.
3) Передача потокового діаграма - графічне відображення послідовності операцій в рамках окремого процесу, із зазначенням альтернативних шляхів розвитку подій в разі виконання або невиконання певних умов.
фрагмент діаграми <Прием продукции на склад>.
4) Схема Ісікава (причинно-наслідковий діаграма) показана на рис. 5, дозволяє формалізувати і структурувати причини виникнення тієї чи іншої події, наприклад, - появи невідповідності, а також встановлювати причинно-наслідкові зв'язки.
Всі можливі причини класифікуються за принципом <5М>:
1. Man (Людина) - причини, пов'язані з людським фактором
2. Machines (Машини, обладнання) - причини, пов'язані з обладнанням
3. Materials (Матеріали) - причини, пов'язані з матеріалами
4. Methods (Методи) - причини, пов'язані з технологією роботи, з організацією процесів
5. Measurements (Вимірювання) - причини, пов'язані з методами вимірювання.
Досліджуване подія зображується в правій частині схеми, символізуючи корінь деревовидної діаграми, яка будується праворуч від позначення події. Горизонтально, від кореня діаграми до лівого краю аркуша, наноситься центральна вісь діаграми, схожа на стовбур дерева. До центральної осі діаграми К. Ісікава примикають п'ять гілок, кожна з яких відповідає своєму класу причин, або своєму <М>.
Причинно-наслідковий діаграма К. Ісікава
Далі, на кожній гілці окремо, як на осі, будуються додаткові <веточки>, кожна з яких представляє окрему причину в своєму класі. До кожної такої <веточке>, в свою чергу, підводяться пагони-причини більш високого рівня, які деталізують її. Продовжуючи таким чином, ми отримуємо розгалужене дерево, що зв'язує причини настання тієї чи іншої події, що знаходяться на різному рівні деталізації. Таким чином, ми можемо встановити причинно-наслідковий зв'язок між приватними відхиленнями від норми (первинними причинами) і їх впливом на ймовірність настання конкретної події.
Для ефективності застосування даного методу і достовірності отриманих результатів побудова діаграми К. Ісікава повинні виконувати професіонали. Через своєї структури діаграма К. Ісікава також носить назву <рыбья кость>.
5) Діаграма Парето. або ABC-аналіз, дозволяє виявити основні причини, які надають найбільший вплив на виникнення тієї чи іншої ситуації. Принцип Парето свідчить, що 20% причин породжує 80% наслідків. Іншими словами, з усіх можливих причин всього лише 20% є особливо значущими, так як вони впливають на результати, які складають 80% від усієї кількості.
Принцип Парето ще носить назву <Правило 20-80>. Цей принцип названий так на честь італійського економіста Вільфредо Парето, який в кінці XIX-го століття звернув увагу на той факт, що 80% італійського капіталу зосереджено в руках 20% населення Італії. Пізніше справедливість цього правила була підтверджена спостереженнями і подальшими підрахунками результатів в різних галузях життя. Так, усунення 20-ти відсотків із загального числа що виникають невідповідностей відволікає на себе 80% від загальної суми витрат на усунення всіх можливих невідповідностей; для компанії-постачальника 20% із загального числа замовників формують 80% прибутку, і так далі. Таким чином, зосередивши свій вплив на 20% причин, ми впливаємо на 80% наслідків. Наступні 30% причин породжують, як не дивно, тільки 15% наслідків і, нарешті, що залишилися 50% впливають лише на 5% наслідків (рис. 6). Таким чином, ми можемо розподіляти свою увагу і вплив, виходячи із значущості та ефективності результатів.
Наприклад, якщо взяти довільний текст і порахувати, скільки разів в ньому зустрічається кожна буква, то з великою часткою ймовірності виявиться, що букви, що становлять 20% алфавіту, утворюють близько 80% всього тексту.
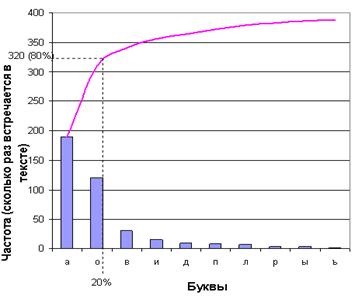
Діаграма В. Парето
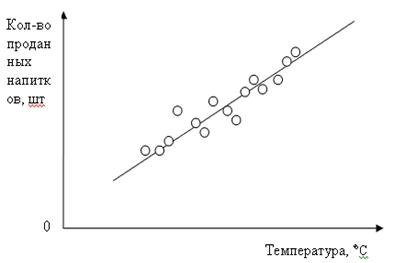
6) Діаграма кореляції (діаграма розсіювання) - графічне відображення відношення між змінними величинами, пов'язаними між собою. Слово «кореляція» (correlation) означає співвідношення, відповідність. Зв'язок, що виявляється при великій кількості спостережень у вигляді певної залежності між середнім значенням результативної ознаки і ознаками-факторами, називається кореляційної.
Діаграма кореляції покликана виявити принцип, за яким змінюється умовно залежна змінна величина при зміні значення незалежної змінної. Наприклад, на малюнку показано, як змінюється обсяг продажу газованих напоїв при зміні погодних умов. У наявності сильна позитивна кореляція.
Коефіцієнт Фехнера (коефіцієнт кореляції знаків) - найпростіший показник тісноти зв'язку. Він заснований на порівнянні поведінки відхилення індивідуальних значень кожної ознаки (X і Y) від своєї середньої величини. При цьому до уваги ухвалюються не величини відхилень (Xi - X) і (Yi - Y). а їх знаки ( «+» або «-»). Визначивши знаки відхилення від середньої величини в кожному ряду, розглядають всі пари знаків і підраховують число їх збігів і розбіжностей. Якщо збіг знаків позначити символом C. а розбіжностей - H. то коефіцієнт Фехнера можна записати як відношення різниці чисел пар збігів і розбіжностей знаків до їх суми, тобто до загальної кількості спостережуваних одиниць:
Очевидно, що якщо знаки всіх відхилень за кожною ознакою співпадуть, то ΣH = 0 і тоді K ф = 1. Це характеризує наявність прямого зв'язку. Якщо все знаки не співпадуть, то ΣC = 0 і тоді K ф = - 1 (зворотний зв'язок). Якщо ж ΣC = ΣH. то K ф = 0, зв'язок відсутній. Отже, як і будь-який показник тісноти зв'язку, коефіцієнт Фехнера може приймати значення від 0 до ± 1. При цьому, чим ближче значення до 1, тим більше (сильніше) тіснота залежності між X і Y. Для наведеного прикладу K ф = 0,8 .
Паралельне розгляд X і Y у n одиниць
Для цього одиниці спостереження розташовують по зростанню значень факторної ознаки X і потім порівнюють з ним поведінку значень результативної ознаки Y.
Обсяг випуску продукції X i
Вартість нереалізованої продукції Y i