Типи даних і робота з ними
Системи комп'ютерної математики, як і будь-які інші програмні засоби, працюють з даними і здійснює їх обробку. Оскільки СКМ орієнтовані на підготовку документів самого різного характеру (у тому числі електронних документів і книг), то вони володіє великим набором можливих типів даних і засобами для роботи з ними. У цьому розділі розглянуто типи даних систем Maple 9.5 / 10 і робота з ними.
Алфавіт Maple-мови (як вхідного, так і програмування) містить 26 малих латинських букв (від а до z), 26 великих латинських букв (від А до Z), 10 арабських цифр (від 0 до 9) і 32 спеціальних символу (арифметичні оператори +, -, *, /, знак зведення в ступінь ^ і ін.). Крім того, є безліч особливих математичних символів. Всі вони будуть описані в цьому розділі. Для введення символів використовується клавіатура і панелі математичних символів.
Є п'ять пар альтернативних символів (що означають одне і теж):
До спеціальних одиночним і складовим знаків відносяться такі елементи синтаксису мови:
•% - системна змінна, що зберігає результат попередньої операції;
•. - фіксатор виразу, що запобігає висновок результату обчислення в комірку виводу;
•; - фіксатор виразу, що дає висновок результату обчислення в комірку виводу;
• `- обмежувач рядка (наприклад` string`);
•: = - оператор присвоювання (наприклад х: = 5);
•. - покажчик типу змінної (наприклад, n :: integer або z :: complex);
• \ - знак зворотного розподілу, який має множинні значення в залежності від контексту (див. Довідку з цього знаку - backslash).
Зарезервовані слова використовуються для створення умовних виразів, циклів, процедур і керуючих команд. Список зарезервованих слів в системі Maple, даний нижче.
and Break by Catch description
do Done elif Else end
error Export fi Finally for
from Global if ln intersect
local Minus mod module next
not Od option options or
proc Quit read Return save
stop Then to Try union
Цими словами можна називати об'єкти користувача.
Сукупність правил, за якими записуються визначення всіх об'єктів Maple-мови, називається його синтаксисом. Деякі особливості синтаксису корисно знати вже на початку освоєння Maple. Наприклад, то що знак - (мінус) має подвійне значення. Стосовно до одного числа, змінної або виразу він змінює їх знак. Однак два знака мінус поспіль (наприклад, в запису --3) задавати не можна. Інше призначення знака мінус - створення операції віднімання, наприклад, 5-2 або а-b. Відповідно подвійне призначення має і знак +, причому число без знака вважається позитивним, так що + 5 = 5.
При введенні дійсних чисел з порядком для вказівки порядку використовується символ ^ (наприклад, 2 * 10 ^ 100 або 2 * 10 ^ -100). Для зведення числа в ступінь поряд з оператором ^ можна використовувати і складовою оператор ** (дві зірочки поспіль). Для зміни загальноприйнятого пріоритету обчислень використовуються круглі дужки, в них же задаються параметри функцій і процедур. Більш докладно синтаксис Maple-мови розглядається нижче.
Деякі оператори представлені двома символами - наприклад, оператор присвоювання змінним їх значення: = містить двокрапку і знак рівності. У таких операторах між символами неприпустимий знак пробілу. Однак його можна використовувати між окремими частинами виразів - так, (a + b) / c еквівалентно (a + b) / c.
Maple забезпечує цілком природну роботу з цілими числами. Зокрема забезпечується зміна знака числа і виконання основних арифметичних операцій з числами. З огляду на загальновідомості арифметичних операцій їх визначення не наводяться. Обмежимося прикладами простих операцій з числами, наведеними нижче:
Результати операцій з цілими числами в загальному випадку представляються раціональними числами. є відносинами цілих чисел.
Десяткова точка в числах має особливий статус - вказівка її в будь-якому місці числа, в тому числі в кінці, робить число речовим і веде до переведення обчислень в режим роботи з речовими числами. наприклад:
.3600000000 10 -13
Кількістю виведених після десяткового дробу цифр можна управляти, задаючи значення системної змінної оточення Digits:
> Digits: = 10; ехр (1.);
Digits: = 102.718281828
> Digits: = 40: evalf (Pi);
Як видно з цих прикладів, введення і виведення чисел має такі особливості:
• для відділення цілої частини мантиси від дробу використовується розділова точка;
• нульова мантиса не відображається (число починається з точки розділення);
• мантиса відокремляться від порядку прогалиною, який розглядається як знак множення;
• уявна частина комплексних чисел задається множенням її на символ уявної одиниці I (квадратний корінь з -1);
• по можливості Maple представляє чисельний результат у вигляді точного раціонального числа (відносини двох цілих чисел).
Для роботи з числами Maple має безліч функцій. Вони будуть розглянуті в подальшому. За допомогою багатофункціональної функції convert Maple може перетворювати числа з різним підставою (від 2 до 36, в тому числі бінарні і шістнадцяткові) в десяткові числа:
> Convert ( "11001111", decimal, binary);
> Convert ( "1AF.С", decimal, hex);
> Convert ( "Maple", decimal, 36);
Завдяки можливості виконання символьних обчислень Maple, як і інші СКА, реалізує точну арифметику. Це означає, що результат може бути отриманий з будь-яким числом точних цифр. Однак треба пам'ятати, що ідеально точні чисельні обчислення виконуються тільки в разі цілочисельних операцій, наприклад, таких як наведено нижче:
942594775983835942085162312448293674956231279470254376832 \ 788935341697759931622147650308786159180834691162349000 \ 3549599583369706302603264000000000000000000000000
Зверніть увагу на те, що в останньому прикладі точність різко втрачена, так як показник ступеня 100.0 було поставлено як число з плаваючою крапкою. Відповідно і результат виявився в формі такого числа. Число вірних цифр результату задає системна змінна Digits (за замовчуванням 10).
Наведемо ще кілька прикладів точних обчислень деяких функцій (з точністю до 150 знаків мантиси):
0.84147098480789650665250232163029899962256306079837106567 \ 275170999191040439123966894863974354305269585434903790 \ 7920674293259118920991898881193410327729
Розробники систем Maple і Mathematica стверджують, що в принципі можливі обчислення і з плаваючою точкою з завданням до мільйона точних цифр мантиси. Практично така точність майже ніколи не потрібна, принаймні для фізиків і інженерів. Наприклад, всього 39 точних цифр числа π досить, щоб обчислити довжину кола всьому Всесвіті з точністю до діаметра атома водню. Однак справжні математики у свій час були просто «схиблені» на обчисленні числа π з великою точністю. Дехто витратив на це все життя. Видатний внесок у такі розрахунки вніс Рамануджан, який ще в 1916 році запропонував алгоритми і формули для обчислення числа π з довільною точністю.
На рис. 2.1 представлено завдання однієї з найвідоміших формул Рамануджана. Уже перший член суми цієї формули (k = 1) дає значення числа π з похибкою обчислення менше 3 # 8729; 10 -8. Збільшення k на 1 кожен раз збільшує число вірних десяткових знаків на 8, т. Е. В сто мільйонів разів! В принципі ця формула може дати до мільярда і більш точних знаків числа π!
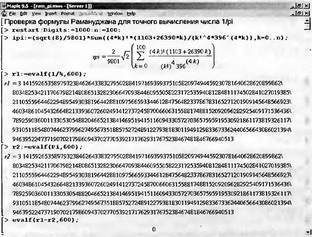
Мал. 2.1. Перевірка обчислень за формулою Рамануджана
У інженерів формула Рамануджана може викликати напад головного або зубного болю. Аж надто безглузда вона з першого погляду. Про яку точність можна говорити, якщо на переважній більшості мов програмування корінь квадратний з двох, факторіал і ступінь обчислюються за все з 8-15 точними знаками?
Але, системи Maple 9.5, завдяки вбудованому апарату точної арифметики, здатна забезпечити ефективну перевірку подібних формул. У нашому випадку ми обмежилися випадком n = 100 (максимальне значення k) і провели обчислення «всього» 600 цифр числа π - з тим, щоб результати вмістилися в один малюнок. І вони говорить сам за себе - все цифри при обчисленні числа π за формулою Рамануджана і по вбудованому в Maple алгоритму повністю співпали, а обчислена помилка дорівнює нулю!
Maple, природно, як і інші СКМ, може працювати з комплексними числами виду z = Re (z) + I # 8729; Im (z). Уявна одиниця в комплексному числі (корінь квадратний з -1) позначається як I. Функції Re (z) і Im (z) повертають дійсну і уявну частини комплексних чисел. На комплексній площині числа задаються координатами точок (х, у) - рис. 2.2.

Мал. 2.2. Подання звичайних і комплексних чисел на площині
Для представлення чисел на рис. 2.2 використовується функція pointplot (list), де list - список координат точок. Ця функція стає доступною при підключенні пакета plots командою with (plots). Крім того, використана функція виведення ряду графічних об'єктів на один графік - display (див. Далі опис уявлення комплексних чисел).
Приклади завдання комплексного числа і виведення його дійсної і уявної частин представлені нижче:
Комплексні числа зазвичай представляють на так званій комплексної площині, у точок якої координата x задає дійсну частину комплексного числа, а у (уявна вісь) показує уявну частину такого числа. На рис. 2.2 показано завдання у вигляді радіус-векторів комплексного числа z = 4 + 3I, -z і комплексно-сполученого числа 4-3I. А на рис. 2.3 показаний приклад обчислення коренів рівняння z ^ n = 1 для випадку n = 16 (інші випадки читач може розглянути самостійно, просто змінивши n). Неважко помітити, що корені рівняння - комплексні числа і що на комплексній площині вони лягають на окружність одиничного радіуса.

Мал. 2.3. Обчислення коренів рівняння z ^ n = 1 і розташування коренів на комплексній площині
Окружність радіуса представляє абсолютне значення комплексного числа z = a + b * I. Вона є геометричним безліччю комплексних чисел, утворених кінцем обертається радіус-вектора числа z навколо його початку в точці (0, 0) комплексної площини, ілюстрацією чого і є окремий приклад рис . 2.2. Пізніше ми розглянемо ряд функцій для роботи з комплексними числами.
Числа можуть служити об'єктами введення, виведення і константами, які входять в математичні вирази. Функція type (x, numeric) дозволяє з'ясувати, чи є х числом. Якщо є, то вона повертає логічне значення true (істина), а якщо немає, то false (брехня). наприклад: