Для визначення , в принципі, досить знати величини R при двох різних температурах. Однак, вибираючи з отриманих результатів довільним чином різні пари значень опору, ми будемо отримувати різні значення .
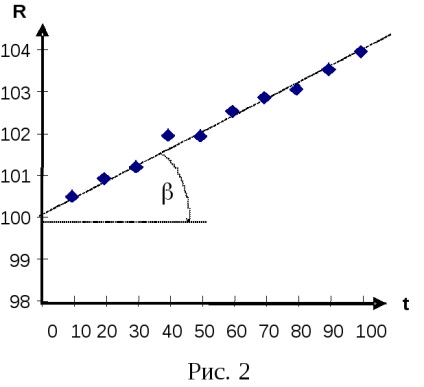
Так як залежність R від t повинна носити лінійний характер, то графік повинен мати вигляд прямої лінії. Оскільки експериментальні крапки не лежать на прямій, то проведемо графік з таким розрахунком, щоб отримані точки розташовувалися в основному рівномірно по обидва боки від графіка.
Графік перетне вісь ординат в точці, що відповідає значенню R0. тобто опору при t = 0 C 0. Для знаходження з графіка необхідно також визначити тангенс кута нахилу прямої. Справді, з формули (8) маємо:
Як зрозуміло з малюнка 2:
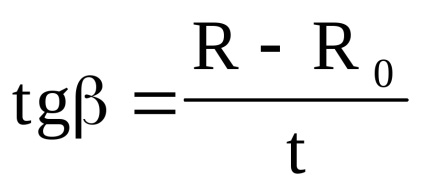
Для знаходження tg найзручніше користуватися формулою (9), підставляючи в неї отримані з графіка величини (R-R0) і t. Графічне зображення результатів досвіду дає також можливість оцінити точність окремих вимірів. Так ясно, що точка графіка, в якій R = 101,9 Ом, t = 40 0 С швидше за все отримана неправильно, тому що вона знаходиться від графіка на відстані більшій, ніж потрійна помилка у визначенні R. Тому при побудові графіка в визначенні ця точка повинна бути відкинута.
Знаходження температурного коефіцієнта опору за допомогою графіка є одним із способів вирішення завдання про одночасне використання всіх експериментальних даних. При цьому ми переконалися, що отримані дані не суперечать формулою (8), змогли без складних обчислень знайти , швидко виявили невірний результат і виключили його вплив на остаточний результат.
Обробка даних за допомогою графіка істотно полегшилася завдяки тому, що шукана залежність має прямолінійний характер. Провести пряму через експериментальні точки не становить труднощів. А як провести, наприклад, найкращу параболу або синусоїду? Для цього треба так вибрати масштаб по осях графіка, щоб очікувана теоретична залежність мала вигляд прямої лінії. Так, наприклад, якщо ви вимірюєте прискорення тіла по відстані S, пройденого тілом за час t, то зв'язок цих величин дається формулою:
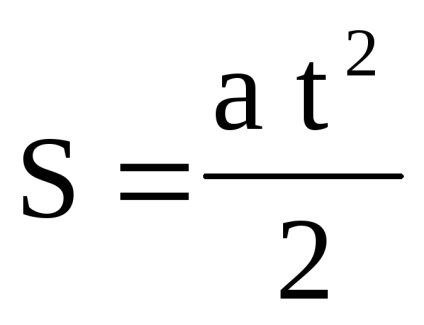
Якщо по осях графіка відкладати S і t, то експериментальні точки розташуються поблизу параболи, провести на око яку дуже важко. Справа істотно полегшиться, якщо по осях відкладати S і t 2. або і t, або, нарешті їх логаріфмиlnS і lnt. У всіх цих випадках експериментальні точки розташуються близько прямої лінії, яку неважко провести на-віч з достатньою точністю.
Лабораторна робота № 1
Тема: «Вимірювання лінійних величин»
Тема «Вимірювання лінійних величин» є основоположною при вивченні практичної фізики.
Ознайомитися з методами вимірювання лінійних величин
Навчиться використовувати штангенциркуль і мікрометр
Ознайомитися з методами обробки експериментальних даних і оцінки точності вимірювань.
Устаткування: штангенциркуль, мікрометр, вимірювані тіла.
План вивчення теми:
Контроль вихідного рівня знань.
- індивідуальний усне опитування, фронтальне опитування.
Основні поняття і положення теми
Ноніусом називають доповнення до звичайного масштабу, що дозволяє підвищити точність вимірювання з даними масштабом в 10-20 разів.
Лінійний ноніус - це маленька лінійка, яка може ковзати уздовж великої лінійки, званої масштабом. Поділу на ноніус наносяться зазвичай так, що одну поділку ноніуса становить (m - 1) / m = 1 - 1 / m частину поділів масштабу, де m- число поділок ноніуса.

Мал. 1. Лінійний ноніус.
Аналогічним чином можна будувати не тільки лінійні, але і кутові ноніуси. Ноніус забезпечуються штангенциркулі (рис. 2), теодоліти і багато інших прилади.
Штангенциркуль (рис. 2) має, крім основних поділів на штанзі, другу шкалу поділок - ноніус по внутрішньому краю рамки. Якщо ніжки приладу щільно зімкнуті, початкові поділу обох шкал збігаються; при цьому легко помітити, що дев'яти розподілам основної шкали (а) відповідають десять поділок ноніуса (b).
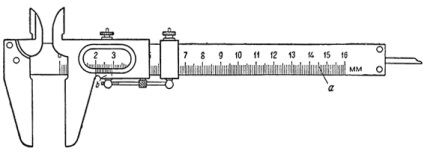
Мал. 2. Штангенциркуль.
Кожне ділення ноніуса одно 0,9 поділки основної шкали. Таким чином, різниця між розподілами основної шкали і поділами ноніуса становить 0,1 поділки основної шкали.
Розглянемо приблизну процедуру вимірювання за допомогою збільшеної моделі ноніуса на малюнку 3.
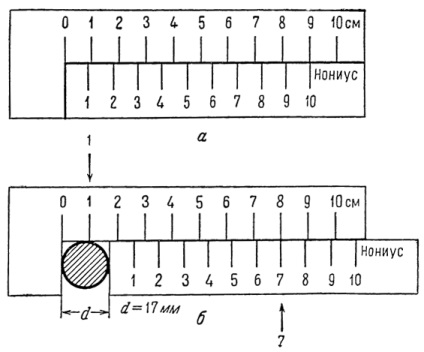
Мал. 3. Модель ноніуса і хід вимірювань:
а - нульове положення; б - схема вимірювання.
Перевівши ноніус (рис. 3, а) в положення, при якому його нульове ділення збігається з нульовим діленням основної шкали, легко виявити різницю в 0,1 см на кожному сантиметрі основної шкали. При всіх переміщеннях ноніуса одне з його поділів буде збігатися з якимось з ділень основної шкали. Щоб визначити шуканий розмір, досить подивитися, яке ділення ноніуса збіглося з діленням основної шкали, і встановити його порядковий номер. Це дасть число десятих часток поділки основної шкали. На малюнку 3 б дано вимір діаметра валика. Легко встановити, що величина діаметра лежить між 1 і 2 см. Так як 7-е поділ ноніуса збігається з одним з ділень основної шкали, в нашому випадку з 8-м, то шуканий вимірюваний діаметр d = 1,7 см.
Мікрометричний гвинт. Мікрометр.
При точних вимірах відстаней нерідко застосовують мікрометричні гвинти - гвинти з малим і дуже точно витриманим кроком. Такі гвинти вживаються, наприклад, в точних вимірювальних приладах (мікроскоп, мікрометр) і дозволяє проводити вимірювання до сотих часток міліметра. (Рис. 4). Один поворот гвинта мікрометра пересуває його стрижень на 0,5 мм. Барабан, пов'язаний зі стрижнем, розбитий на 50 поділок. Поворот на одну поділку відповідає зсуву стержня на 0,01 мм. З цієї точністю зазвичай і проводять виміри за допомогою мікрометра. Мікрометричний гвинт являє собою стрижень, забезпечений точної гвинтовою нарізкою.
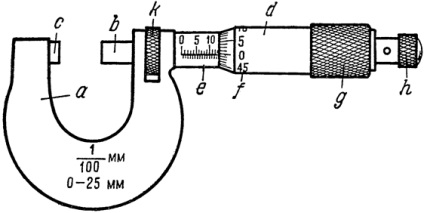
Мал. 4. Микрометр. а - скоба; b - вимірювальна головка; з - п'ята; d - барабан з лімбом (кругова шкала); е - стебло з міліметровою шкалою; f - лімб з відліком до 0,01 мм; g - рифлений барабан; h - тріскачка, k- стопор.
Висота підйому гвинтової нарізки за один оборот називається кроком мікрометричного гвинта. Мікрометр (рис. 4) складається з двох основних частин: скоба a і мікрометричний гвинт (вимірювальна головка) b. Мікрометричний гвинт проходить через отвори скоби з внутрішнім різьбленням, проти мікрометричного гвинта на скобі є упор (або п'ята). На мікрометричного гвинта закріплений повний циліндр (барабан) з поділами по колу. При обертанні мікрометричного гвинта барабан ковзає по лінійної шкалою, нанесеною на стеблі.
Для того, щоб мікрометричний гвинт b пересунувся на 1 мм, необхідно зробити два оберти барабана d. Таким чином, крок мікрометричного гвинта дорівнює 0,5 мм. У мікрометра на барабані d є шкала (лімб), що містить зазвичай 50 поділок. Так як крок гвинта s = 0,5 мм, а число поділок барабана m = 50, то точність мікрометра складає
s / m = 0,5 / 50 = 1/100 мм. (1)
У підсумку, числове значення довжини вимірюваного предмета мікрометрів або штангенциркулем знаходять
де q- ціле число мм масштабної лінійки, n - ділення ноніуса, яке збігається з будь-яким розподілом масштабної лінійки, s / m -точність.
Результат можна сформулювати наступним чином: довжина зразка, яка вимірюється за допомогою ноніуса, дорівнює числу цілих поділок масштабу плюс точність ноніуса, помножена на номер поділки ноніуса збігається з деяким розподілом масштабу.