Хлопці, ми з вами побудували багато графіків функцій, наприклад, параболи, гіперболи, графіки тригонометричних функцій і інші. Давайте згадаємо, як ми це робили. Ми вибирали точки на осі абсцис, вираховували значення ординат нашої функцій і плавно з'єднували наші ординати на координатної площині. Тобто, ми будували графік по точках. При побудові багатьох графіків, точки потрібно вибирати обдумано. Тепер давайте узагальнимо наші знання і напишемо загальні правила побудови графіків функцій.
Що ж таке графік функції?
Графік функції - це безліч точок, абсциси яких є значеннями з області визначення, а ординати - значеннями функції y = f (x). Графік будь функцій будують по точках. Але якщо ми точно не знаємо, якою буде вид у графіка, то точки треба вибирати обдумано. Хлопці, які важливі точки є у функцій?
Давайте, згадаємо їх:
а) Стаціонарні та критичні точки. Такі точки ми навчилися знаходити при обчисленні екстремумів функцій. Це точки, в якій похідна або дорівнює нулю, або не існує.
б) Точки екстремуму. Точки максимуму і мінімуму функцій. Точки, біля яких визначається характер монотонності.
в) Точки перетину графіка з віссю абсцис і віссю ординат. Значення, в яких функція y = f (x) = 0 - точки перетину з віссю абсцис. А якщо обчислити f (0) - то ця точка перетину з віссю ординат.
г) Точки розриву функцій. Ці точки шукаються для не наскрізною функцій.
Правило побудови графіків функцій
Хлопці, давайте запишемо основні правила побудови графіків функцій:
- Якщо функція y = f (x) неперервна на всій числовій прямій, то треба знайти стаціонарні і критичні точки, точки екстремуму, проміжки монотонності, точки перетину графіка з осями координат і при необхідності вибрати ще кілька контрольних точок, в яких слід підрахувати значення нашої функції .
- Якщо функція y = f (x) визначена не на всій числовій прямій, то починати слід з знаходження області визначення функції, з вказівки точок її розриву.
- Корисно досліджувати функцію на парність, оскільки графіки парній або непарній функцій мають симетрією (відповідно щодо осі y або щодо початку координат), і, отже, можна спочатку побудувати тільки гілка графіка при x ≥ 0, а потім домалювати симетричну гілку.
- Якщо то пряма y = b є горизонтальною асимптотой нашого графіка функції. Асимптота - це деякою орієнтир для нашої функції. Це те, до чого прагне графік функції в точці, але не досягає цього значення.
- Якщо f (x) = $ \ frac $; і при x = a знаменник звертається в нуль, а чисельник відмінний від нуля, то x = a - це вертикальна асимптота.
Кілька правил, що спрощують побудову графіків функцій:
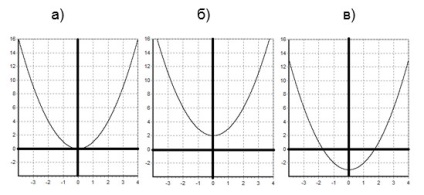
а) Графік функції y = f (x) + a виходить з графіка функції y = f (x) (графік y = f (x) заздалегідь відомий), шляхом паралельного перенесення графіка y = f (x) на а одиниць вгору, якщо а> 0; і на а одиниць вниз, якщо а 2. б) y = x 2 + 2, в) y = x 2 - 3.
Графіки наших функцій виходить з графіка функції y = x 2. шляхом його паралельного перенесення: б) на дві одиниці вгору, в) на три одиниці вниз.
Графіки наших функцій:
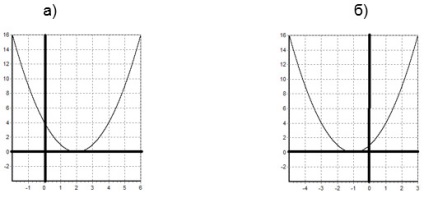
б) Графік функції y = f (x + a) виходить з графіка функції y = f (x) (графік y = f (x) заздалегідь відомий). Використовуємо паралельний перенос графіка y = f (x) на а одиниць вліво, якщо а> 0, і на а одиниць вправо, якщо а 2. б) y = (x + 1) 2.
Графіки наших функцій виходить з графіка функції y = x 2. шляхом його паралельного перенесення: б) на дві одиниці вправо, в) на одну одиницю вліво.
Графіки наших функцій:
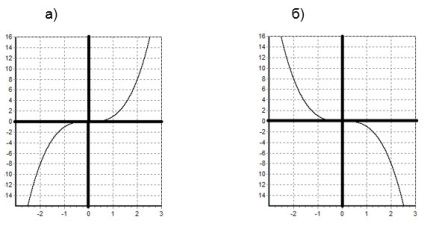
в) Для побудови графіка функції y = f (-x), слід побудувати графік функції y = f (x) і відобразити його відносно осі ординат. Отриманий графік є графіком функції y = f (-x).
Для прикладу побудуємо два графіки: a) y = x 3. б) y = (-x) 3.
Графіки нашої функцій виходить з графіка функції y = x 3. шляхом відображення щодо осі ординат.
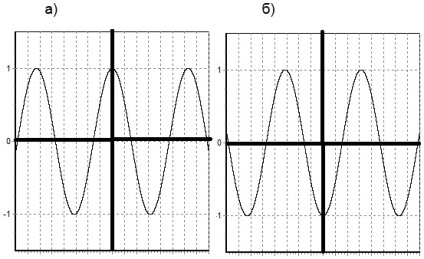
г) Для побудови графіка функції y = -f (x) слід побудувати графік функції y = f (x) і відобразити його відносно осі абсцис.
Для прикладу побудуємо два графіки: a) y = cos (x), б) y = -cos (x). Графіки нашої функцій виходить з графіка функції y = cos (x), шляхом відображення щодо осі абсцис.
Хлопці, тепер давайте побудуємо графіки функцій, вид яких заздалегідь не відомий. Будемо використовувати правила, які ми визначили на початку.
Приклади на побудову
I. Побудувати графік функції: y = 2x 2 + 4x - 5.
Рішення:
1) Область визначення: D (y) = (-∞; + ∞).
2) Знайдемо стаціонарні точки:
y '= 4x + 4,
4x + 4 = 0,
x = -1.
3) Визначимо вид стаціонарної точки і характер монотонності:
Точка x = -1 - точка мінімуму. Знайдемо значення функції в точці x = -1
y (-1) = 2 (-1) 2 + 4 (-1) - 5 = -7.
Отже, наша функція спадає на проміжку = (- ∞; -1), x = -1 - точка мінімуму, функція зростає на проміжку (-1; + ∞).
Обчислимо значення функції в парі точок:
Побудуємо графік функції:
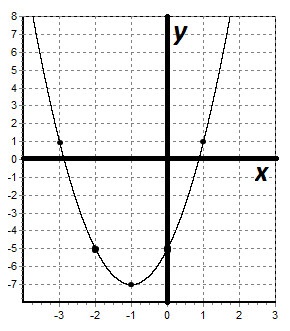
II. Побудувати графік функції: y = 5x 3 - 3x 5.
Рішення:
1) Область визначення: D (y) = (-∞; + ∞).
2) Знайдемо стаціонарні точки:
y '= 15x 2 - 15x 4,
y '= 15x 2 (1 - x 2) = 15x 2 (1 - x) (1 + x),
15x 2 (1 - x) (1 + x) = 0,
x = 0; ± 1.
3) Визначимо вид стаціонарної точки і характер монотонності:
Точка x = -1 - точка мінімуму.
Точка x = 0 - точка перегину, функція в цій точки так само зростає, але увігнутість змінюється в іншу сторону.
Точка x = 1 - точка максимуму.
Знайдемо значення функції в точці x = -1: y (-1) = 5 (-1) 3 - 3 (-1) 5 = -2.
Знайдемо значення функції в точці x = 0: y (0) = 5 (0) 3 - 3 (0) 5 = 0.
Знайдемо значення функції в точці x = 1: y (1) = 5 (1) 3 - 3 (1) 5 = 2
5) Досліджуємо функцію на парність: y (-x) = 5 (-x 3) - 3 (-x 5) = -5x 3 + 3 5 = -y (x)
За визначенням функція непарна, і графік симетричний відносно початок координат.
Отже, функція непарна.
Наша функція спадає на проміжку рівному (-∞; -1).
x = -1 - точка мінімуму. Функція зростає на (-1; 1).
x = 0 - точка перегину.
x = 1 - точка максимуму. Функція зростає на (1; + ∞).
Обчислимо значення функції в парі точок:
Побудуємо графік функції:
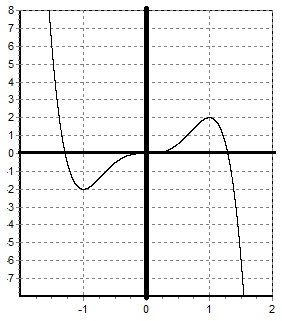
III. Побудувати графік функції: y = $ \ frac $.
Рішення:
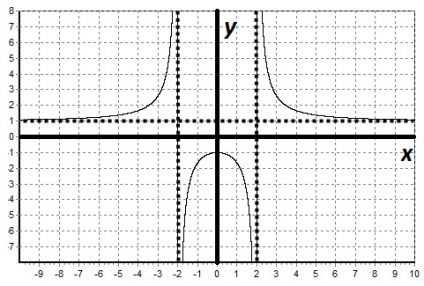
1) Область визначення: D (y) = (-∞; -2) U (-2; 2) U (2; + ∞).
За визначенням функція парна. Значить, графік функції симетричний відносно осі ординат, можна спочатку побудувати графік функції для x ≥ 0. 3) Пряма x = 2 - вертикальна асимптота, тому що знаменник нашої функції в цій точці звертається в нуль.
Знайдемо горизонтальну асимптоти:
Пряма y = 1 - горизонтальна асимптота.
4) Знайдемо стаціонарні і критичні точки:
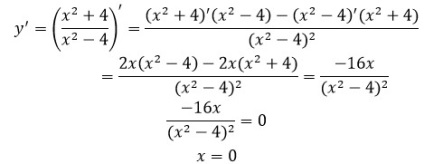
5) Визначимо вид стаціонарної точки і характер монотонності: Точка x = 0 - точка максимуму.
Отже, наша функція парна. Вона зростає на проміжку рівному (-∞; 0), x = 0 - точка максимуму. Функція убуває на (0; + ∞).
Пряма x = 2 - вертикальна асимптота. Пряма y = 1 - горизонтальна асимптота.
Обчислимо значення функції в парі точок:
Оскільки функція парна побудуємо спочатку графік для x ≥ 0.
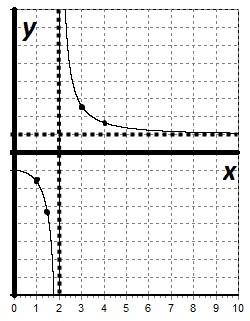
Використовуючи властивість парних функцій, відобразимо графік функції щодо осі ординат.
Завдання на побудову графіків функцій для самостійного рішення
1) Побудувати графік функції: $ y = (-x) ^ 2 + 4x - 7 $.
2) Побудувати графік функції: $ y = x ^ 3 - 3x + 2 $.
3) Побудувати графік функції: $ y = \ frac $.