Гравітаційне поле, або поле тяжіння - фізичне поле, через яке здійснюється гравітаційна взаємодія [1].
Гравітаційне поле в класичній фізиці
Закон всесвітнього тяжіння
Закон тяжіння Ньютона
В рамках класичної фізики гравітаційна взаємодія описується «законом всесвітнього тяжіння» Ньютона, згідно з яким сила гравітаційного тяжіння між двома матеріальними точками з масами і пропорційна обом масам і обернено пропорційна квадрату відстані між ними:
Тут - гравітаційна стала, приблизно рівна м³ / (кг с?), - відстань між точками.
Для розрахунку поля в більш складних випадках, коли тяжіють маси не можна вважати матеріальними точками, можна скористатися тим фактом, що поле ньютоновского тяжіння потенційно. Якщо позначити щільність речовини # 961 ;, то потенціал поля # 966; удовлетворяетуравненію Пуассона:
Недоліки ньютонівської моделі тяжіння
Практика показала, що класичний закон всесвітнього тяжіння дозволяє з величезною точністю пояснити і передбачити руху небесних тіл. Однак ньютонівська теорія містила ряд серйозних недоліків. Головний з них - незрозуміле дальнодействие: сила тяжіння передавалася невідомо як через абсолютно порожній простір, причому нескінченно швидко. По суті ньютонівська модель була суто математичною, без будь-якого фізичного змісту. Крім того, якщо Всесвіт, як тоді припускали, евклидова і нескінченна, і при цьому середня щільність речовини в ній ненульова, то виникає гравітаційний парадокс: потенціал поля всюди звертається в нескінченність. В кінці XIX століття виявилася ще одна проблема: помітна розбіжність теоретичного і спостережуваного зсуву перигелію Меркурія.
Протягом понад двісті років після Ньютона фізики пропонували різні шляхи удосконалення ньютонівської теорії тяжіння. Ці зусилля увінчалися успіхом в 1915 році, зі створенням загальної теорії відносності Ейнштейна, в якій всі зазначені труднощі були подолані. Теорія Ньютона виявилася наближенням більш загальної теорії, які можуть застосовуватися при виконанні двох умов:
Гравітаційний потенціал в досліджуваній системі не надто великий (багато менше).
Швидкості руху в цій системі незначні в порівнянні зі швидкістю світла.
Напруженість гравітаційного поля - векторна величина, що характеризує гравітаційне поле в даній точці і чисельно дорівнює відношенню сили тяжіння, що діє на тіло, поміщене в дану точку поля, до гравітаційної масі цього тіла:
Якщо джерелом гравітаційного поля є якесь гравитирующего тіло, то відповідно до закону всесвітнього тяжіння:
- гравітаційна маса тіла-джерела поля;
- відстань від досліджуваної точки простору до центру мас тіла-джерела поля.
Застосовуючи другий закон Ньютона і принцип еквівалентності гравітаційної та інерційної мас:
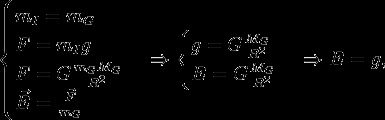
тобто напруженість гравітаційного поля чисельно (і по розмірності) дорівнює прискоренню вільного падіння в цьому полі.
Гравітаційний потенціал - скалярна функція координат і часу, що характеризує гравітаційне поле в класичній механіці. Має розмірність квадрата швидкості, зазвичай позначається буквою. Гравітаційний потенціал дорівнює відношенню потенційної енергії матеріальної точки, розміщеної в розглянуту точку гравітаційного поля, до маси цієї точки. Вперше поняття гравітаційного потенціалу ввів в науку Адрієн Марі Лежандр в кінці XVIII століття.
Гравітаційний потенціал і рівняння руху [ред | правити вихідний текст]
Рух частинки в гравітаційному полі в класичній механіці визначається функцією Лагранжа, що має в інерціальній системі відліку вигляд:
. де: - маса частинки, - координата частинки, - потенціал гравітаційного поля.
Підставляючи вираз для лагранжиана L в рівняння Лагранжа:
,
отримуємо рівняння руху
.