На рис. 337 зображений один виток гвинтової поверхні. утвореної рухом відрізка АВ. Пряма, що визначається даними відрізком, у всіх положеннях перетинає вісь під одним і тим же кутом (на рис. 337 кут 60 °). Переміщення кінців відрізка уздовж осі пропорційно кутовому переміщенню відрізка.
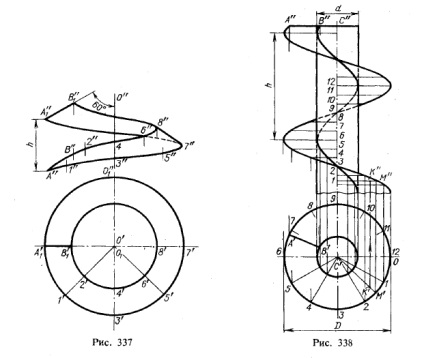
Точки А і В утворюють циліндричні гвинтові лінії, як і всі точки відрізка АВ, і, отже, для більш точного зображення нарису гвинтової поверхні на пл. π2 треба було б провести щонайбільше проекцій гвинтових ліній, описуваних різними точками відрізка АВ, і потім провести криві, що огинають ці проекції. Практично замість цього громіздкого побудови зазвичай проводять прямі, одночасно стосуються проекцій гвинтових ліній (див. Рис. 345). Якщо нахил утворює по відношенню до осі циліндра НЕ дорівнює 90 ° (наприклад, 60 ° на рис. 337), то гвинтова поверхня носить назву косою. Якщо ж цей кут дорівнює 90 °, то утворюється пряма гвинтова поверхня. Вона показана на рис. 338.
За своєю освітою поверхню, зображена на рис. 338, є коноїд. Дійсно, утворює - пряма лінія; вона у всіх положеннях паралельна деякій площині (в даному випадку перпендикулярної до осі циліндра): утворює перетинає дві напрямні лінії, криву і пряму (вісь циліндра). Так як крива напрямна являє собою кручені лінію, то такий коноїд називається гвинтовим. Інша назва - прямий гелікоїд 1).
На рис. 338 гвинтовий коноїд показаний спільно з круговим циліндром, що має спільну з ним вісь; в результаті на поверхні циліндра утворюється циліндрична гвинтова лінія, крок якої однаковий з кроком направляючої гвинтовий лінії. Поверхня, укладену між обома гвинтовими лініями, називають кільцевим гвинтовим коноїд.
Зображена на рис. 337 поверхню, яка називається косою гвинтовий, носить також назву косого гелікоїда. Характерним для такої поверхні є те, що прямолінійна твірна перетинає в усіх своїх положеннях напрямні - циліндричну гвинтову лінію і пряму лінію (вісь поверхні), причому утворює перетинає вісь під постійним кутом, не рівним 90 °. У всіх положеннях утворює паралельна утворюючим деякого конуса обертання. вісь якого збігається з віссю гвинтовий лінії (рис. 339, зліва). Якщо, наприклад, треба отримати фронтальну проекцію утворює косого гелікоїда, що проходить через точку С, то слід почати з проведення горизонтальної проекції цієї утворює, т. Е. Провести радіус S'C ', по якій точці С'1 знайти точку С "1 і фронтальну проекцію утворює SC1. конуса, а потім провести C "D" паралельно S "C" 1.
На рис. 339 праворуч показана гвинтова поверхня, утворена рухом відрізка, дотичного до поверхні циліндра. Побудова зводиться знову до знаходження проекцій
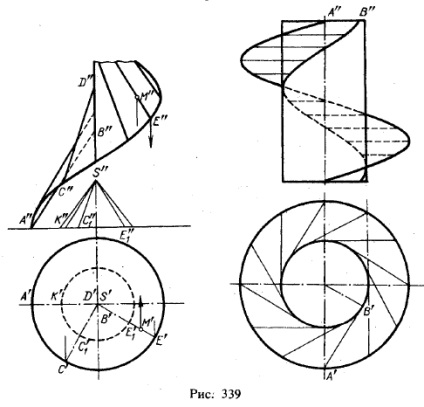
гвинтових ліній, утворених двома точками: кінцем А відрізка і точкою дотику В. Відрізок може бути спрямований по відношенню до осі або під прямим кутом (як взято на рис. 339), або під гострим.
1) Helicoidal (фр.) - гвинтовий; helice (фр.) - спіраль, гвинтова лінія. Кажуть також гелісоід. Під гелісоідом розуміють лінійчату кручені поверхню.
Поверяность, зображена на рис. 339 справа, є циліндроїда (див. С. 143). Дійсно, утворює у всіх положеннях залишається паралельної деякій площині і ковзає по двох напрямних - просторовим кривим; площину паралелізму перпендикулярна до осі циліндра; утворює стосується поверхні циліндра (точки дотику утворюють циліндричну гвинтову лінію) і в той же час перетинає направляючу кручені лінію, вісь якої збігається, віссю циліндра. Поверхня, зображену на рис. 339 справа, називають гвинтовим циліндроїда. Якщо утворює такій поверхні, схрещували з віссю циліндра, становить з цією віссю кут, рівний 90 °, то поверхня вже не відноситься до розряду циліндроїда, вона носить назву косого кільцевого гелікоїда.
Розглянуті гвинтові поверхні відносяться до розряду неразвертиваемих. Але є гвинтова поверхня, яка розглядається як розгортається. Це - поверхня з ребром повернення, яким є циліндрична гвинтова лінія (див. Рис. 317). Таку кручені поверхню називають розверзається гелікоїда.
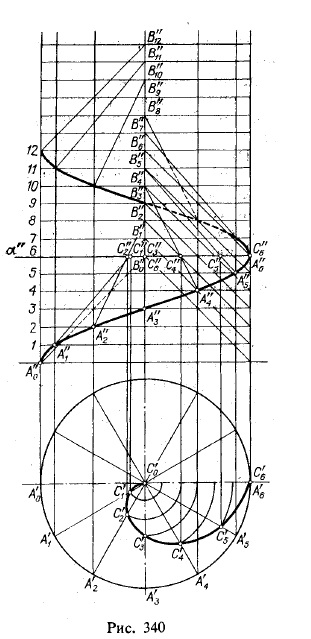
На рис. 340 поверхню косого гелікоїда показана в перетині з пл. α, перпендикулярній до осі цієї поверхні; крива перетину зображена на пл. π1. без спотворення, так як α || π1. Ця крива є спіраллю Архімеда 1).
Побудова цієї кривої зводиться до наступного. Розбивши кут А'0 С'0 С'6 (180 °) на кілька (в даному випадку на шість) рівних частин, на стільки ж рівних між собою частин розбиваємо і відрізок С'0 С'6. На радіусі С'0 А'1 від точки С'0 відкладаємо, на радіусі С'0 А'2 відкладаємо С'0 С'2 = 2C'0 C'1 і т. Д.
Тепер звернемо увагу на те, як будуються проекції точок, що належать прямій і косою гвинтовим поверхням.
Для прямої гвинтової поверхні це показано на рис. 338. Покладемо, що точка К, що належить поверхні, задана горизонтальною проекцією К '. Щоб знайти проекцію К ", треба провести горизонтальну проекцію тієї утворює, на якій повинна знаходитися точка К, т. Е. Провести радіус СМ 'через проекцію К'. По-якій точці М 'знаходимо точку М" і проводимо фронтальну проекцію цієї утворює, паралельну А "В". На цій прямій знаходимо проекцію К "2).
Якщо буде дана проекція К "і треба знайти К ', то спочатку через К" проводимо пряму перпендикулярно до осі гвинтової лінії до перетину з проекцією гвинтовий лінії в точці М ", по цій точці знаходимо точку М' і на радіусі С'М '- точку К '.
Точність побудови тут пов'язана з точністю проведення синусоїди (фронтальній проекції гвинтової лінії), так як точка М "знаходиться на ній.
1) Тих, хто цікавиться доказом відсилаємо до попередніх видань.
2) Зверніть увагу на видимість точки К по відношенню до пл. π2. при «непрозорості» гвинтової поверхні точка К невидима.
У разі косою гвинтової поверхні (рис. 339, зліва), якщо Дайан проекція М 'і треба знайти М ", проводимо через точку М' радіус E'S ', по точкам Е' і Е'1 знаходимо точки Е" і Е "1. проводимо проекцію S "E" 1 утворює конуса і паралельно їй через точку Е "проекцію утворює гвинтової поверхні. На цій проекції отримуємо проекцію М ".
Якщо ж задається проекція М "і треба знайти М ', то доводиться побудувати криву (спіраль Архімеда) від перетину косою гвинтової поверхні площиною, проведеної на рівні точки М" перпендикулярно до осі поверхні, і на спіралі знайти точку М'.
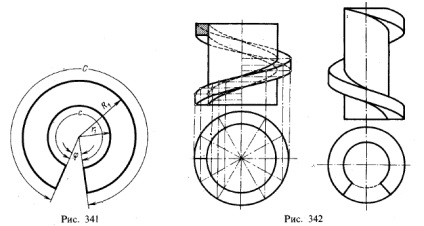
Гвинтові поверхні, зазначені на рис. 337 - 340, не можуть бути точно розгорнуті на площині. Для прямої гвинтової поверхні, зображеної на рис. 338, можна наближено розгорнути кожен окремий оборот так, як це показано на рис. 341. Розгортка одного обороту може бути представлена (груба результати) як частина плоского кільця.
Для побудови такої частини кільця потрібно знайти величину радіусів R1 і г1 і кут φ. Якщо крок гвинтової поверхні (рис. 338) позначити через h, а діаметри зовнішній і внутрішній (діаметр циліндра) - через D і d, то за формулою, зазначеною на с. 133, довжини ділянок гвинтових ліній виразяться так:
Так як гвинтові лінії розгортаються в даному випадку в концентричні дуги при одному і тому ж центральному куті, то c: C = r1: Ri і, отже,
Позначимо ширину гвинтової поверхні, т. Е. Різницю. через a, одержуємо R1 = r1 + а, звідки Звідси випливає, що кут φ може бути визначений з формули
Покладемо D = 100 мм, d = 60 мм, h = 50 мм. Знаходимо а = 20 мм, С≈318 мм, с≈195 мм, r1 ≈32 мм, R1 ≈52 мм, φ≈10 °.
Проводимо радіусами R1 = 52 мм і г1 = 32 мм дві концентричні кола, будуємо центральний кут φ = 10 ° і таким чином виділяємо частину кільця, що представляє собою (груба результати) розгортку одного обороту гвинтової поверхні.
Маючи кілька таких розгорнутих оборотів, можна кожен оборот з'єднати з циліндричним стрижнем діаметра d (як це показано на рис. 343) і скріпити між собою один за іншим навернені на стрижень обертів.
Подібно до того, як при гвинтовому русі точки утворюється гвинтова лінія і при гвинтовому русі відрізка прямої виходить гвинтова поверхня, можна отримати гвинтове тіло, якщо змусити будь-яку плоску фігуру (наприклад, квадрат, трикутник, трапецію) рухатися по поверхні циліндра так, щоб вершини цієї фігури переміщалися по гвинтових лініях, а площину самої фігури постійно проходила через вісь циліндра. Утворюється гвинтовий виступ, обмежений гвинтовими і циліндричними поверхнями. Побудова проекцій такого гвинтового виступу зводиться до побудови стількох гвинтових ліній, скільки вершин у вибраній фігури.
На рис. 342 зліва показано побудова гвинтового виступу, утвореного рухом квадрата. Квадрат весь час примикає однією своєю стороною до котра утворює циліндра; вершини квадрата рухаються по гвинтових лініях.
При нарізуванні різьблення гвинтовий виступ (виток) утворюється видаленням за допомогою ріжучого інструменту частині матеріалу.
Отриманий гвинтовий виступ обмежений дцумя прямими гвинтовими поверхнями і двома циліндричними поверхнями, зовнішньої і внутрішньої, що стикається з поверхнею самого циліндра. Сукупність циліндра і гвинтового виступу на ньому називають гвинтом. У разі, зображеному на рис. 342 зліва, дан гвинт з правого різьбленням. підйом гвинтового виступу на передній (видимої) стороні циліндра йде зліва направо. Якби підйом гвинтового виступу на передній (видимої) стороні циліндра йшов справа наліво (рис. 342, праворуч), то гвинт був би з лівою різьбою (див. С. 133, права і ліва гвинтові лінії).
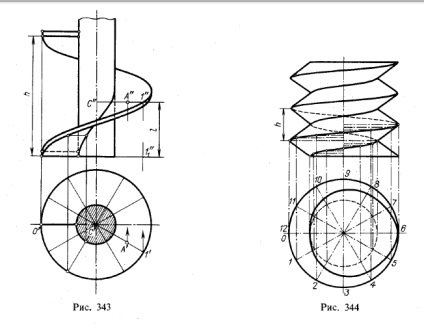
На рис. 343 показаний гвинтовий виступ, утворений рухом прямокутника, що примикає до котра утворює циліндра своєї меншої стороною. Гвинти такого виду застосовуються в гвинтових транспортерах 1).
На цьому ж кресленні показано побудова проекції А "точки А, що знаходиться на гвинтової поверхні і заданої проекцією А '. Побудова подібно вказаною на рис. 338, але показано, як уникнути неточності в проведенні синусоїди. Для цього можна визначити відрізок l, що визначає переміщення точки 1 уздовж осі гвинта при повороті утворює з початкового положення в положення С1 (тобто на кут О'С'1 '). Треба взяти пропорцію х. h = ∠О'С'1'. 360 °, звідки визначити х, що і дасть нам величину l. Подальше ясно з креслення.
Гвинти, зображені на рис. 342, мають квадратну різьблення. Якщо замість квадрата взяти трикутник і змусити його переміщатися уздовж циліндра так само, як це було зроблено з квадратом, то отримаємо гвинт з трикутної різьбленням (рис. 344). Виробляє трикутник примикає однією стороною до основного циліндра; вершини трикутника утворюють гвинтові лінії, для отримання яких взяті дві окружності. Ці кола розділені на 12 частин; точки поділів спроектовані на горизонтальні лінії, проведені через 12 поділок кроку гвинта. Поверхня гвинта з трикутної різьбленням є поєднанням двох косих гвинтових поверхонь. Відомий контур на пл. π2 отриманий шляхом проведення дотичних до проекція великої і малої гвинтових ліній (рис. 345). Так зазвичай і роблять, хоча насправді контур проекції косою гвинтової поверхні на пл. π2 є криву лінію.
На рис. 346 показано побудову поперечного перерізу гвинта з трикутної різьбленням площиною α. Проведена допоміжна горизонтально-проектує площину β, що проходить через вісь гвинта. У перетині з гвинтовим виступом пл. β виділяє виробляє трикутник 2), горизонтальна проекція якого розташовується на горизонтальному сліді пл. π; фронтальна проекція боку АВ цього трикутника перетинається зі слідом α "в точці К", що представляє собою фронтальну проекцію однієї з точок, що належать лінії перетину гвинтової поверхні пл. α. На відрізку А'В 'виходить горизонтальна проекція точки К, що належить горизонтальній проекції шуканої лінії перетину гвинтової поверхні пл. α.
1) Гвинтовий транспортер (шнек), інакше гвинтовий конвеєр, застосовується для переміщення зерна, дрібнокускових матеріалів і т. П.
2) Площина β виділяє виробляє трикутник в двох його положеннях; на передній (видимої) і задньої (невидимої) сторони гвинта. На рис. 346 показано побудову для передньої (видимої) сторони гвинта.
6 В. О. Гордон, М. А. Семенцов-Огієвський
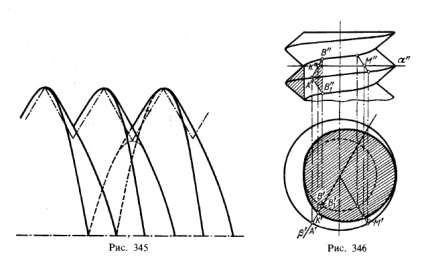
Далі, побудована ще одна точка М (М ", М ') цього перетину; на цей раз горизонтально-проектує площину не проведено, щоб показати, що цілком достатньо намітити лише положення горизонтальної проекції виробляє трикутника, провівши один з радіусів. Також замість повної фронтальної проекції проводить трикутника досить обмежитися проекцією однієї його сторони, як це показано на рис. 346.
Проводячи ряд радіусів і, побудувавши відповідні їм положення виробляє трикутника, отримаємо ряд точок для проведення горизонтальної проекції контуру перетину. Каті видно, фігура перетину обмежена кривою лінією, що має вісь симетрії; отже, можна при побудові обмежитися перебуванням лише однієї половини кривої лінії,
а іншу частину її будувати як симетричну гілку. Кожна половина цієї кривої лінії являє собою спіраль Архімеда, про побудову якої сказано на с. 159.
У гвинті, представленому на рис. 344, що виробляє трикутник після кожного обороту навколо осі основного циліндра піднімається в суміжне положення на величину кроку гвинтової лінії. Гвинт виходить від руху одного профілю. Такий гвинт називається одноходовой 1).
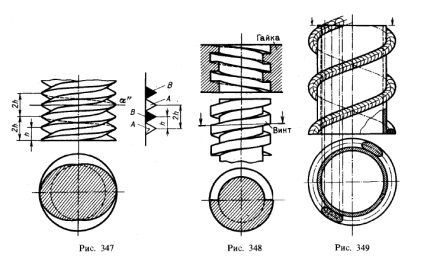
Якщо взяти два профілі і, вважаючи їх з'єднаними між собою, змусити рухатися по гвинтових лініях так, щоб кожен профіль після одного обороту піднімався на висоту 2h (рис. 347), то вийде двухходовой гвинт 2).
На рис. 348 зображені гвинт з правого квадратної різьбленням і гайка до нього. На горизонтальному розрізі видно відрізки прямих, що обмежують разом з півкола фігуру перерізу. Ці відрізки відповідають тому, що гвинтовий виступ обмежений не косою, а прямий гвинтовою поверхнею.
На рис. 349 показаний двухходовой гвинт двогвинтового транспортера 3), утворений навиванні сталевого дроту круглого перетину на сталеву трубу; дріт кріпиться на трубі зазвичай зварюванням.
Представляючи собі ряд сфер, діаметр яких дорівнює діаметру дроту і центри яких поміщаються на гвинтовий лінії (осі витка), контур проекції витка окреслюємо як лінію, що огинає окружності - проекції сфер.
На горизонтальній проекції показані перетину двох витків (контур проекції перетину побудований як лінія, обгортають окружності, одержувані при перетині зазначених вище сфер площиною).
Питання до § 52
- Як утворюються пряма і коса гвинтові поверхні?
- Чому пряма гвинтова поверхня називається також гвинтовим коноїд?
- Що являє собою кільцевої гвинтовий коноїд?
- Як утворюється гвинтовий циліндроїда?
1) одноходовой гвинти називаються іноді однооборотний, однозаходний, гвинтами в одну нитку.
2) Інші назви: двухоборотний, двухзаходная, гвинт в дві нитки.
3) Двогвинтовий транспортер служить для переміщення штучних вантажів, наприклад мішків, пакунків і т. П.