Ідеальна оптична система зображує точку у вигляді точки, тобто всі промені, які виходять з будь-якої точки предмета, збираються після виходу з системи в одній точці зображення.
Іншими словами подідеальной оптичною системою розуміють таку оптичну систему, яка не порушує гомоцентрічності пройшли через неї променів. Теорія ідеальної оптичної системи розроблена Гауссом і має чисто геометричний характер.
Реальні оптичні системи, що складаються зі сферичних і плоских заломлюючих і відбивають, в загальному випадку не задовольняють положенням теорії ідеальних оптичних систем. Зображенням світиться точки на екрані в реальному оптичній системі буде не крапка, а світла пляма.
Реальні оптичні системи поводяться як ідеальні лише для променів, що розповсюджується вздовж осі центрованої оптичної системи, коли промені утворюють дуже малі кути з оптичною віссю і нормалями до заломлюючим і відображає поверхонь системи.
У цьому випадку (якщо e << 1рад) і, користуючись розкладанням в ряд Тейлора функцій sin e:
Область, в межах якої можна робити такі заміни, називається параксіальної, а відповідні пучки променів називають параксіальними (або нульовими). У цій області закон заломлення світла можна записати в наступному вигляді:
Лінійне, кутове і поздовжнє збільшення оптичної системи
Виберемо в предметній площині Q перпендикулярної оптичної осі відрізок довжиною y. Його зображення буде розташовано в сполученої плоскостіQ ¢ і матиме лінійні размериy ¢ (рис.4).
Ставлення розміру зображення до розміру предмета називають лінійним збільшенням оптичної системи (b):
Для пари сполучених площин Q і Q 'перпендикулярних оптичній осі лінійне збільшення постійно і не залежить від величини предмета. при
b> 0 зображення перевернуте, при b <0 - зображення пряме.
Рис.4. До визначення збільшення оптичної системи.
Кутовим збільшенням оптичної системи (¡) Називають відношення тангенсів кутів утворених сполученими променями з оптичною віссю:
Поздовжнім збільшенням оптичної системи (a) називають відношення розміру зображення нескінченно малого відрізка, розташованого вздовж оптичної осі, до розміру цього відрізка:
Кардинальні елементи оптичної системи
Ідеальна оптична система має низку кардинальних елементів - передній і задній фокуси, передні і задні головні і вузлові точки, передні і задні фокальні і головні площини, переднє і заднє фокусні відстані.
Знання чотирьох кардинальних точок (зазвичай це фокуси і головні точки) повністю визначає роботу оптичної системи, тобто ми можемо побудувати зображення будь-якої точки, користуючись тільки кардинальними елементами і абсолютно не розглядаючи дійсного ходу променів в даній оптичній системі.
2.5.1. Задній фокус і задня фокальна площина оптичної системи.
Заднім фокусом оптичної системи називають зображення нескінченно віддаленої точки, розташованої на оптичній осі.
Промені, що виходять з нескінченно віддаленої точки на оптичній осі, падають на оптичну систему паралельно оптичної осі. Тому можна сказати, що заднім фокусом оптичної системи називається точка (F '), в якій збирається пучок променів, що падають на систему паралельно її оптичній осі (рис.5).
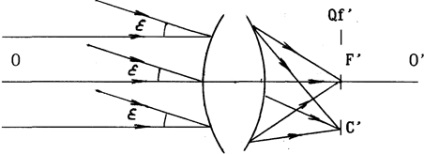
Рис.5. Задній фокус і задня фокальна площина оптичної системи.
Площина (Qf), що проходить через задній фокус і перпендикулярна оптичній осі, називаетсязадней фокальною площиною оптичної системи. Ця площина є зображенням нескінченно віддаленої площині.
Паралельний пучок променів, що падає на оптичну систему під кутом до оптичної осі (e), йде з нескінченно віддаленої точки, розташованої поза оптичної осі, і після виходу з оптичної системи збирається в сполученої точкеС ', яка знаходиться поза оптичної осі, в задній фокальній площині .