А. Ейнштейн заклав основи спеціальної теорії відносності (СТО). Ця теорія являє собою сучасну фізичну теорію простору і часу, в якій, як і в класичній ньютонівської механіці, передбачається, що час однорідне, а простір однорідний і изотропно. Спеціальна теорія відносності часто називається також релятивістської теорією. а специфічні явища, що описуються цією теорією, - релятивістськими ефектами.
В основі спеціальної теорії відносності лежать постулати Ейнштейна. сформульовані ним в 1905 р
I. Принцип відносності: ніякі досліди (механічні, електричні, оптичні), проведені всередині даної системи відліку, не дають можливості виявити, спочиває чи ця система або рухається рівномірно і прямолінійно; всі закони природи інваріантні по відношенню до переходу від однієї системи відліку до іншої.
II. Принцип інваріантності швидкості світла: швидкість світла у вакуумі не залежить від швидкості руху джерела світла спостерігача й однакова у всіх інерціальних системах відліку.
Перший постулат Ейнштейна, будучи узагальненням механічного принципу відносності Галілея на будь-які фізичні процеси, стверджує, таким чином, що фізичні закони інваріантні по відношенню до вибору системи відліку, а рівняння, що описують ці закони, однакові за формою в усіх інерційних системах відліку. Відповідно до цього постулату, все інерціальні системи відліку зовсім рівноправні, т. Е. Явища (механічні, електродинамічні, оптичні та ін.) У всіх інерційних системах відліку протікають однаково. Відповідно до другого постулату Ейнштейна, сталість швидкості світла - фундаментальна властивість природи, яке констатується як досвідчений факт.
Спеціальна теорія відносності зажадала відмови від звичних уявлень про простір і час, прийнятих в класичній механіці, оскільки вони суперечили принципу сталості швидкості світла. Втратило сенс не тільки абсолютний простір, але і абсолютний час.
Постулати Ейнштейна і теорія, побудована на їх основі, встановили новий погляд на світ і нові просторово-часові уявлення, такі, наприклад, як відносність довжин і проміжків часу, відносність одночасності подій.
Згідно з уявленнями класичної механіки, маса тіла є величина попостоянная. Однак в кінці XIX століття на дослідах з швидко рухомими електронами було встановлено, що маса тіла залежить від швидкості його руху, а
саме зростає зі збільшенням швидкості за законом
де - маса спокою матеріальної точки, т. е. маса, виміряна в тій інерціальній системі відліку, щодо якої матеріальна точка знаходиться в спокої; с - швидкість світла у вакуумі; - маса точки в системі відліку, щодо якої вона рухається зі швидкістю. Отже, маса однієї і тієї ж частинки різна в різних інерційних системах відліку.
З принципу відносності Ейнштейна, який стверджує інваріантність усіх законів природи при переході від однієї інерціальної (Инвариантность - це незмінність, сталість; незалежність) системи відліку до іншої, слід умова
інваріантності рівнянь фізичних законів щодо перетворень Лоренца.
Основний закон динаміки Ньютона: виявляється також інваріантним по відношенню до перетворень Лоренца, якщо в ньому справа стоїть похідна за часом від релятивістського імпульсу.
Основний закон релятивістської динаміки матеріальної точки має вигляд
(2), або (3), де (4) - релятивістський імпульс матеріальної точки.
В силу однорідності простору в релятивістській механіці виконується закон збереження релятивистского імпульсу. релятивістський імпульс замкнутої системи зберігається, т. е. не змінюється з плином часу. Часто взагалі не обмовляють, що розглядають релятивістський імпульс, так як якщо тіла рухаються зі швидкостями, близькими до. то можна використовувати тільки релятивістське вираз для імпульсу.
Аналіз формул (1), (4) і (2) показує, що при швидкостях, значно менших швидкості світла, рівняння (2) переходить в основний закон класичної механіки (). Отже, умовою застосування законів класичної (ньютонівської) механіки є умова. Закони класичної механіки виходять як наслідок теорії відносності для граничного випадку (формально перехід здійснюється при). Таким чином, класична механіка - це механіка макротел, що рухаються з малими швидкостями (в порівнянні зі швидкістю світла у вакуумі).
Знайдемо кінетичну енергію релятивістської частинки (матеріальної точки).
Приріст кінетичної енергії матеріальної точки на елементарному переміщенні
дорівнює роботі сили на цьому переміщенні: або. (5)
Враховуючи що . і підставивши в (5) вираз (2), отримуємо:.
Перетворивши даний вираз з урахуванням того, що. і формули (1), наведемо до вираження (6),
т. е. приріст кінетичної енергії частинки пропорційно збільшенню її маси.
Так як кінетична енергія частки, що покоїться дорівнює нулю, а її маса дорівнює масі спокою. то, проинтегрировав (6), отримаємо (7), або кінетична енергія релятивістської частинки має вигляд (8).
Вираз (8) при швидкостях переходить в класичне: (розкладаючи в ряд при. Правомірно знехтувати членами другого порядку малості).
А. Ейнштейн узагальнив положення (6), припустивши, що воно справедливо не тільки для кінетичної енергії частинки (матеріальної точки), але і для повної енергії, а саме будь-яка зміна маси супроводжується зміною повної енергії частинки (матеріальної точки): (9).
Звідси А. Ейнштейн прийшов до універсальної залежності між повною енергією тіла і його масою. (10).
Рівняння (10), так само як і (9), висловлює фундаментальний закон природи - закон взаємозв'язку (пропорційності) маси і енергії. повна енергія системи дорівнює добутку її маси на квадрат швидкості світла у вакуумі. Відзначимо, що в повну енергію Е не входить потенційна енергія тіла в зовнішньому силовому полі.
Закон (10) можна, з огляду на вираз (7), записати у вигляді. звідки випливає, що покоїться тіло (Т = 0) також володіє енергією. званої енергією спокою. Класична механіка енергію спокою не враховує, вважаючи, що при енергія покоїться тіла дорівнює нулю.
В силу однорідності часу в релятивістській механіці, як і в класичній, виконується закон збереження енергії. повна енергія замкнутої системи зберігається, т. е. не змінюється з плином часу.
З формул (10) і (4) знайдемо релятивістське співвідношення між повною енергією і імпульсом частинки:. .
Повертаючись до рівняння (10), відзначимо ще раз, що воно має універсальний характер. Воно може бути застосовано до всіх форм енергії, т. Е. Можна стверджувати, що з енергією, якої б форми вона не була, пов'язана маса і, навпаки, з усякою масою пов'язана
певна енергія (10).
Щоб охарактеризувати міцність зв'язку і стійкість системи будь-яких частинок (наприклад, атомного ядра як системи з протонів і нейтронів), розглядають енергію зв'язку. Енергія зв'язку системи дорівнює роботі, яку необхідно затратити, щоб розкласти цю систему на складові частини (наприклад, атомне ядро - на протони і нейтрони). Енергія зв'язку системи. де - маса спокою - ой частки у вільному стані; - маса спокою системи, що складається з частинок.
Закон взаємозв'язку (пропорційності) маси і енергії блискуче підтверджено експериментом про виділення енергії при протіканні ядерних реакцій. Він широко використовується для розрахунку енергетичних ефектів при ядерних реакціях і перетвореннях елементарних частинок.
Електричний диполь. Дія електричного поля на диполь. Електричне поле в діелектриках. Полярні і неполярні молекули. Поляризація діелектриків. Діелектрична проникність.
(1) - принцип суперпозиції (накладення) електричних полів. згідно з яким напруженість Е результуючого поля, створюваного системою зарядів, дорівнює геометричній сумі напруженостей полів, створюваних в даній точці кожним із зарядів окремо.
Принцип суперпозиції дозволяє розрахувати електростатичні поля будь-якої системи нерухомих зарядів, оскільки якщо заряд не точкові, то їх можна завжди звести до сукупності точкових зарядів.
Принцип суперпозиції застосуємо для розрахунку електростатичного поля електричного диполя. Електричний диполь - система двох рівних по модулю різнойменних точкових зарядів (+ Q. - Q), відстань між якими значно менше відстані до розглянутих точок поля. Вектор, спрямований по осі диполя прямої, що проходить через обидва заряду) від негативного заряду до позитивного і дорівнює відстані між ними, називається плечем диполя. Вектор (2) збігається за напрямком з плечем диполя і дорівнює добутку заряду на плече. називається електричним моментом диполя або дипольним моментом (рис.).
Згідно з принципом суперпозиції (1), напруженість Е поля диполя в довільній точці. де і - напруженості полів, створюваних відповідно позитивним і негативним зарядами.
Діелектрик (як і будь-яка речовина) складається з атомів і молекул. Так як позитивний заряд всіх ядер молекули дорівнює сумарному заряду електронів, то молекула в цілому електрично нейтральна. Якщо замінити позитивні заряди ядер молекул сумарним зарядом + Q. що знаходиться в центрі «тяжкості» позитивних зарядів, а заряд всіх електронів - сумарним негативним зарядом - Q. знаходиться в центрі
«Тяжкості» негативнихзарядів, то молекулу можна розглядати як
електричний диполь з електричним моментом, певним формулою (2).
Першу групу, діелектриків (N2. Н2, О2. СО2. СН4.) Складають речовини, молекули яких мають симетричну будову, т. Е. Центри «тяжкості» позитивних і негативних зарядів за відсутності зовнішнього електричного поля збігаються і, отже, дипольний момент молекули р дорівнює нулю. Молекули таких діелектриків називаються неполярними. Під дією зовнішнього електричного поля заряди неполярних молекул зміщуються в протилежні сторони (позитивні по полю, негативні проти поля) і молекула набуває дипольний момент.
Другу групу діелектриків (Н2 О, NH3. SO2. CO.) Складають речовини, молекули яких мають асиметричну будову, т. Е. Центри «тяжкості» позитивних і негативних зарядів не збігаються. Таким чином, ці молекули за відсутності зовнішнього електричного поля мають дипольним моментом. Молекули таких діелектриків називаються полярними. При відсутності зовнішнього поля, однак, дипольні моменти полярних молекул внаслідок теплового руху орієнтовані в просторі хаотично і їх результуючий момент дорівнює нулю. Якщо такий діелектрик помістити в зовнішнє поле, то сили цього поля будуть прагнути повернути диполі вздовж поля і виникає відмінний від нуля результуючий момент.
Третю групу діелектриків (NaCl, КСl, КВг.) Складають речовини, молекули яких мають іонну будову. Іонні кристали являють собою
просторові решітки з правильним чергуванням іонів різних знаків. В цих
кристалах не можна виділити окремі молекули, а розглядати їх можна як
систему двох всунути одна в іншу іонних подрешеток. При накладенні на
іонний кристал електричного поля відбувається деяка деформація кристалічної решітки або відносне зміщення подрешеток, що приводить до виникнення дипольних моментів.
Таким чином, внесення всіх трьох груп діелектриків в зовнішнє електричне поле призводить до виникнення відмінного від нуля результуючого електричного моменту діелектрика, або, іншими словами, до поляризації діелектрика. Поляризацією діелектрика називається процес орієнтації диполів або появи під впливом електричного поля орієнтованих по полю диполів.
Відповідно трьом групам діелектриків розрізняють три види поляризації:
електронна. або деформационная, поляризація діелектрика з неполярними
молекулами, що полягає у виникненні у атомів індукованого дипольного моменту за рахунок деформації електронних орбіт;
орієнтаційна. або дімольная, поляризація діелектрика з полярними молекулами, що полягає в орієнтації наявних дипольних моментів молекул по полю. Природно, що тепловий рух перешкоджає повної орієнтації молекул, але в результаті спільної дії обох факторів (електричне поле і тепловий рух) виникає переважна орієнтація дипольних моментів молекул по полю. Ця орієнтація тим сильніше, чим більше напруженість електричного поля і нижче температура;
іонна поляризація діелектриків з іонними кристалічними гратами, яка полягає в зміщенні підґратки позитивних іонів уздовж поля, а негативних - проти поля, що приводить до виникнення дипольних моментів.
При приміщенні діелектрика в зовнішнє електростатичне поле він поляризується,
т. е. набуває відмінний від нуля дипольний момент. де - дипольний момент однієї молекули. Для кількісного опису поляризації діелектрика користуються векторною величиною - поляризованістю. яка визначається як дипольний момент одиниці об'єму діелектрика:. (2)
З досвіду випливає, що для великого класу діелектриків поляризованность Р лінійно залежить від напруженості поля Е. Якщо діелектрик ізотропний і Е не надто велике, то (3), де діелектрична сприйнятливість речовини, що характеризує властивості діелектрика; - величина безрозмірна; притому завжди> 0 і для більшості діелектриків (твердих і рідких) становить кілька одиниць (хоча, наприклад, для спирту. для води = 80).
Для встановлення кількісних закономірностей поля в діелектрику внесемо в однорідне зовнішнє електростатичне поле (створюється двома нескінченними
паралельними різнойменно зарядженими площинами) пластинку з однорідного діелектрика, розташувавши її так, як показано на рис.
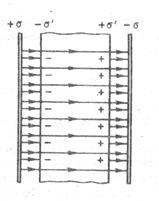
Під дією поля діелектрик поляризується, т. Е. Відбувається зміщення зарядів: позитивні зміщуються по полю, негативні - проти поля. В результаті цього на правій грані діелектрика, зверненого до негативної площині, буде надлишок позитивного заряду з поверхневою щільністю. на лівій - негативного заряду з поверхневою щільністю. Ці НЕ компенсувати заряди, що з'являються в результаті поляризації діелектрика, називаються пов'язаними. Так як їх поверхнева щільність менше щільності вільних зарядів площин, то не всі поле Е компенсується полем зарядів діелектрика: частина ліній напруженості пройде крізь діелектрик, інша ж частина-обривається на пов'язаних зарядах. Отже, поляризація
діелектрика викликає зменшення в ньому поля порівняно з початковим
зовнішнім полем. Поза діелектрика.
Таким чином, поява пов'язаних зарядів призводить до виникнення додаткового електричного поля (поля, створюваного пов'язаними зарядами),
яке спрямоване проти зовнішнього поля (поля, створюваного вільними зарядами) і послаблює його. Результуюче поле всередині діелектрика.
Поле (поле, створене двома нескінченними зарядженими площинами), тому. (4)
Визначимо поверхневу щільність зв'язаних зарядів. По (2). повний
дипольний момент пластинки діелектрика. де S - площа грані пластинки, d - її товщина. З іншого боку, повний дипольний момент, згідно з (3), дорівнює добутку пов'язаного заряду кожної грані на відстань d між ними, т. Е.. Таким чином, . або (5), тобто поверхнева щільність зв'язаних зарядів дорівнює поляризованности Р.
Підставивши в (4) вирази (5) і (3), отримаємо, звідки напруженість результуючого поля всередині діелектрика дорівнює. (6)
Безрозмірна величина (7) називається діелектричною проникністю середовища. Порівнюючи (6) і (7), бачимо, що показує, у скільки разів поле послаблюється діелектриком, характеризуючи кількісно властивість діелектрика поляризуватися в електричному полі.