Імпульс і енергія в спеціальній теорії відносності:
У реляті-вістской механіці виконується закон збереження імпульсу: при будь-яких процесах, що відбуваються в замкну-тій системі, її імпульс (т. Е. Геометрична сума творів релятивістських мас всіх частин цієї системи на їх швидкості) не зміниться-ється. Основне рівняння релятивістської ді-намики має вигляд
- імпульс тіла (матеріальної точки) в релятивістської механіке.Можно показати, що рівняння (7.21) задовольняє вимогу лоренц-інваріантності, якщо при переході від однієї системи відліку до іншої перетворювати компоненти сили уздовж осей координат за певним законом. При малих швидкостях (<<с) масса те-ла mm0 =const и релятивистское уравне-ние (7.21) совпадает с основным законом ньютоновской динамики (2.5), а импульс тела является линейной функцией его скорости: p=m0 v=mv. У всех тел масса покоя m0>0. Тому, як видно з формул (7.20) і (7.22), релятивістська маса і імпульс тіла повинні необмежено зростати при прагненні швидкості тіла до швидкості світла у вакуумі. Всі реальні сили кінцеві по величині, а їх дія на тіло обмежене в време-ні. Вони не можуть повідомити тілу нескінченно великий імпульс. Отже, швидкість тіла по відношенню до будь-якій інерційній системі відліку не може бути дорівнює швидкості світла у вакуумі, а завжди менше її. Це твердження справедливо також для атомів, молекул і всіх елементарних частинок, за винятком фотонів. Знайдемо вираз для кінетичної енергії матеріальної точки в релятивіст-ської механіці. Приріст кінетичної енергії матеріальної точки на елементарний-ном переміщенні dr дорівнює роботі, вдосконалення-Шаєм на цьому переміщенні силою F, що діє на матеріальну точку:
де v-швидкість точки. При зміні швидкості матеріальної точки збільшення її кине-чеський енергії і релятивістської маси про-порційно один одному:
Кінетична енергія покоїться точ-ки ( = 0) дорівнює нулю, а її релятивістська маса дорівнює m0. Тому, проинтегрировав рівняння (7.24) по m від m0 до m, напів-чим такий вираз для кінетичної-ської енергії матеріальної точки:
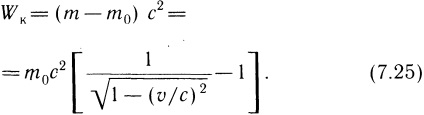
Скористаємося розкладанням в ряд Тейлора:
Е
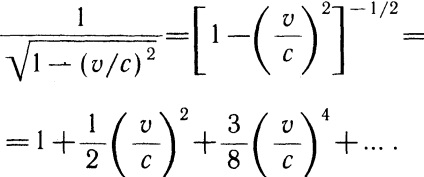
Таким чином, при малих швидкостях руху матеріальної точки її кінетична енергія, обчислена за релятивіст-ської формулою (7.25), збігається з значени третьому цієї енергії в ньютонівської механіці. Однак при великих швидкостях матеріальних-ної точки її кінетична енергія Wк = (m-m0) з 2 відмінна і від m0 2/2, і від m0 2/2. Формули (7.24) і (7.25) справедливий-ви також для системи матеріальних точок (наприклад, твердого тіла), що рухаються як одне ціле зі швидкістю v.