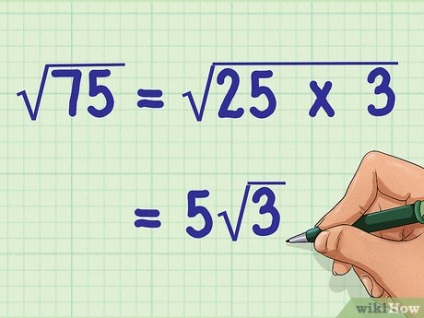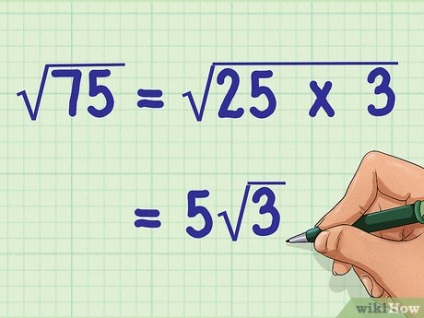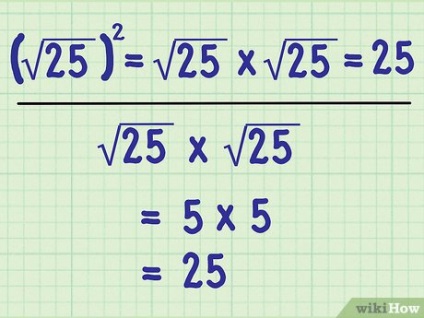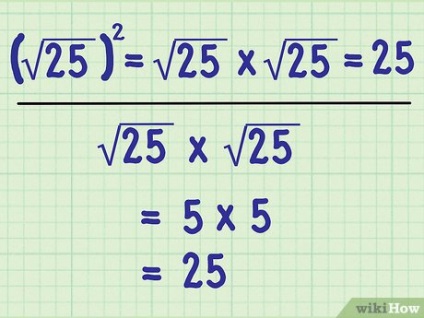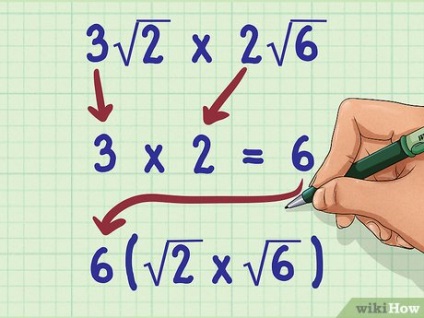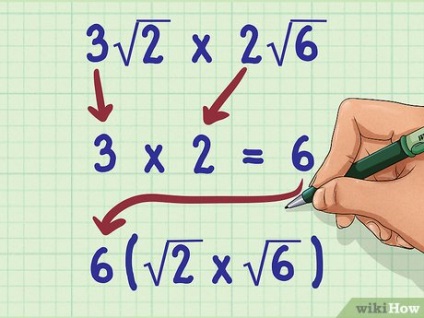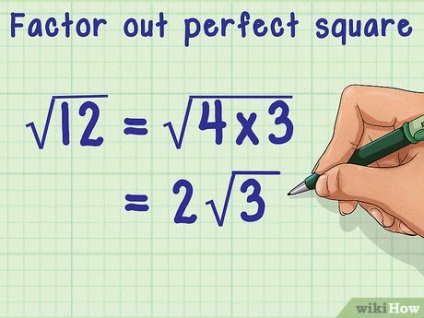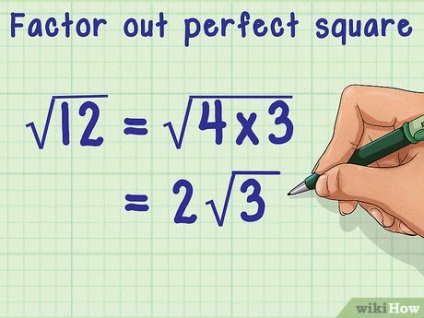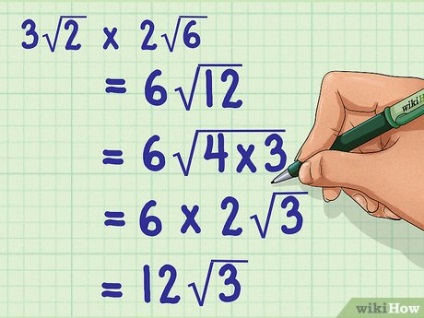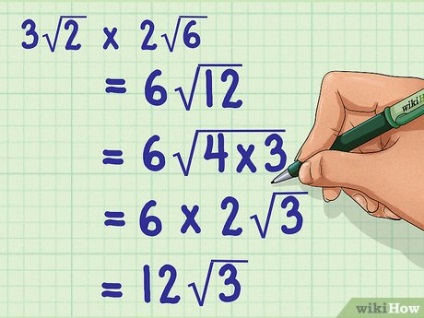Перемножте подкоренное числа. Це числа, які знаходяться під знаком кореня. [1] Перемножте подкоренное числа як цілі числа. Результат множення запишіть під одним знаком кореня. [2]
- Наприклад, 15 × 5> \ times >>. Перемножте подкоренное числа: 15 × 5 = 75. Таким чином, 15 × 5 = 75> \ times> = >>.
Винесіть множник з-під кореня. Для цього з'ясуйте, чи можна розкласти підкореневе число на два множники, один з яких є повним квадратом. [3] Якщо повного квадрата немає, результат спростити не можна; в цьому випадку запишіть його у відповіді.
- Повний квадрат - це число, яке є квадратом (твором самого на себе) цілого числа. [4] Наприклад, 25 - це повний квадрат, тому що 5 × 5 = 25.
- Наприклад, 75 >> можна розкласти на два множники, один з яких (25) є повним квадратом:
75 >>
= 25 × 3 >>
Вийміть квадратний корінь з повного квадрата, а результат запишіть перед знаком кореня. Інший множник залиште під знаком кореня. Так ви спростите подкоренное вираз.
- Наприклад, 75 >> можна розкласти на два множники 25 × 3 >>. Таким чином, з числа 25 можна витягти корінь:
75 >>
= 25 × 3 >>
= 5 3 >>
Зведіть квадратний корінь в квадрат. У деяких завданнях квадратний корінь множиться сам на себе. Зведення в квадрат і витяг квадратного кореня - це дві протилежні операції, тобто вони скасовують один одного. Результатом зведення квадратного кореня в квадрат є підкореневе число. [5]
- Наприклад, 25 × 25 = 25> \ times> = 25>. Ви отримали такий результат, бо 25 × 25 = 5 × 5 = 25> \ times> = 5 \ times 5 = 25>.
Метод 2 з 2:
Перемноження квадратних коренів з множниками Правити
Перемножте множники. Тут множник - це число, яке знаходиться перед знаком кореня. На цьому етапі не звертайте уваги на подкоренное числа - просто перемножте множники. Результат запишіть перед першим знаком кореня.
- При перемножуванні множників не забудьте про їх знаки. Пам'ятайте, що при множенні негативного числа на позитивне вийде негативне число, а при множенні негативного числа на негативне вийде позитивне число.
- Наприклад, 3 2 × 2 6> Параметри \ times 2 >>. Спочатку перемножте множники: 3 × 2 = 6. Таким чином, завдання набуде вигляду: 6 2 × 6> \ times >>.
Перемножте подкоренное числа. Перемножте подкоренное числа як цілі числа. Результат множення запишіть під одним знаком кореня.
- У нашому прикладі 6 2 × 6> \ times >> перемножте подкоренное числа: 2 × 6 = 12. Таким чином, 2 × 6 = 12> \ times> = >>. Завдання набуде вигляду 6 12 >>.
Винесіть множник з-під кореня. Для цього з'ясуйте, чи можна розкласти підкореневе число на два множники, один з яких є повним квадратом. [6] Якщо повного квадрата немає, результат спростити не можна; в цьому випадку запишіть його у відповіді.
- Повний квадрат - це число, яке є квадратом (твором самого на себе) цілого числа. [7] Наприклад, 4 - це повний квадрат, тому що 2 × 2 = 4.
- Наприклад, 12 >> можна розкласти на два множники, один з яких (4) є повним квадратом:
12 >>
= 4 × 3 >>
Вийміть квадратний корінь з повного квадрата, а результат помножте на множник, що стоїть перед знаком кореня. Інший множник залиште під знаком кореня. Так ви спростите подкоренное вираз.
- У нашому прикладі 6 12 >> підкореневе число розкладається на два множники 6 4 × 3 >>. Таким чином, з числа 4 можна витягти корінь, а результат потрібно помножити на 6:
6 12 >>
= 6 4 × 3 >>
= 6 × 2 3 >>
= 12 3 >>
Схожі статті