Як розрахувати послідовність Фібоначчі

Послідовність Фібоначчі - це ряд чисел, в якому кожне наступне число дорівнює сумі двох попередніх чисел. Числові послідовності часто зустрічаються в природі і мистецтві в вигляді спіралей і «золотого перетину». Найпростіший спосіб обчислити послідовність Фібоначчі - це створити таблицю, але такий метод не застосуємо до великих послідовностей. Наприклад, якщо потрібно визначити 100-й член послідовності, краще скористатися формулою Біне.

кроки Правити

Метод 1 з 2:
Таблиця Правити

Намалюйте таблицю з двома стовпцями. Кількість рядків таблиці залежить від кількості чисел послідовності Фібоначчі, які потрібно знайти.

• Наприклад, якщо потрібно знайти п'яте число послідовності, намалюйте таблицю з п'ятьма рядками.
• Використовуючи таблицю, можна знайти якийсь випадковий число без обчислення всіх попередніх чисел. Наприклад, якщо потрібно знайти 100-е число послідовності, потрібно обчислити всі числа: від першого до 99-ого. Тому таблиця може бути застосована тільки для знаходження перших чисел послідовності.

У лівому стовпчику напишіть порядкові номери членів послідовності. Тобто напишіть цифри по порядку, починаючи з одиниці.

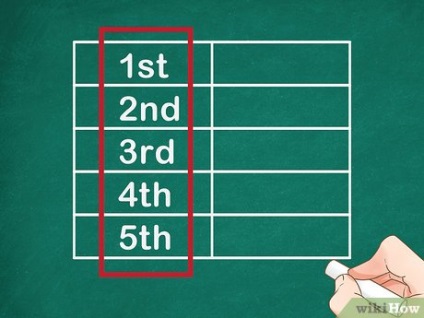
• Такі цифри визначають порядкові номери членів (чисел) послідовності Фібоначчі.
• Наприклад, якщо потрібно знайти п'яте число послідовності, в лівій колонці напишіть наступні цифри: 1, 2, 3, 4, 5. Тобто потрібно знайти з першого по п'яте число послідовності.

У першому рядку правою колонки напишіть 1. Це перше число (член) послідовності Фібоначчі.

• Майте на увазі, що послідовність Фібоначчі завжди починається з 1. Якщо послідовність починається з іншого числа, ви неправильно вирахували все числа аж до першого.

До першого члену (1) додайте 0. Вийде друге число послідовності.

• Запам'ятайте: щоб знайти будь-яке число послідовності Фібоначчі, просто складіть два попередніх числа.
• Щоб створити послідовність, не забудьте про 0, який стоїть перед 1 (першим членом), тому 1 + 0 = 1.

Складіть перший (1) і другий (1) члени. Вийде третє число послідовності.

• 1 + 1 = 2. Третій член дорівнює 2.

Складіть другий (1) і третій (2) члени, щоб отримати четверте число послідовності.

• 1 + 2 = 3. Четвертий член дорівнює 3.

Складіть третій (2) і четвертий (3) члени. Вийде п'яте число послідовності.

• 2 + 3 = 5. П'ятий член дорівнює 5.

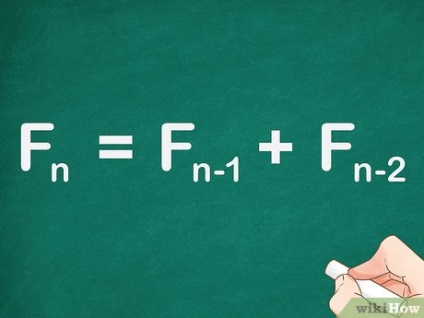
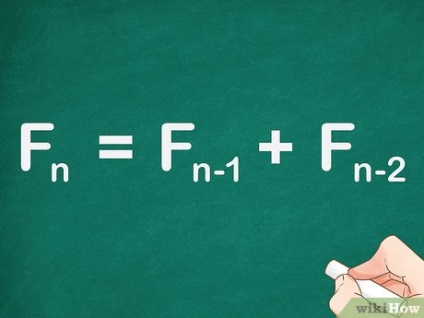
Складіть два попередніх числа, щоб знайти будь-яке число послідовності Фібоначчі. Цей метод заснований на формулі: F n = F n - 1 + F n - 2 = F_ + F_>. [1] Ця формула не є замкнутим, тому за допомогою цієї формули можна знайти будь-який член послідовності без обчислення всіх попередніх чисел.

Метод 2 з 2:
Формула Біне і золотий перетин Правити

Запишіть формулу: x n> = φ n - (1 - φ) n 5 - (1 \ phi) ^ >>>>. У цій формулі x n> - шуканий член послідовності, n - порядковий номер члена, φ - золотий перетин. [2]

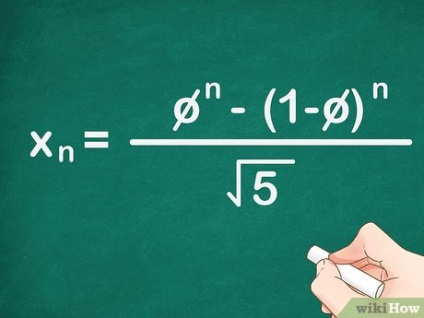
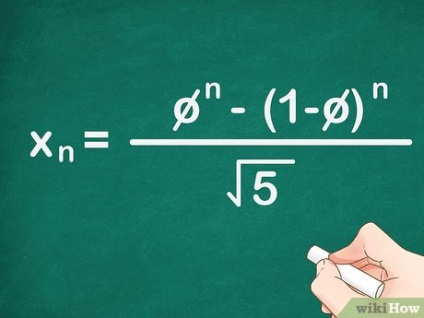
• Це замкнута формула, тому по ній можна знайти будь-який член послідовності без обчислення всіх попередніх чисел.
• Це спрощена формула, отримана з формули Біне для чисел Фібоначчі. [3]
• У формулі присутній золотий перетин (φ), тому що ставлення будь-яких двох послідовних чисел послідовності Фібоначчі дуже схоже на золоте відношення. [4]

У формулу підставте порядковий номер числа (замість n). n - це порядковий номер будь-якого шуканого члена послідовності.

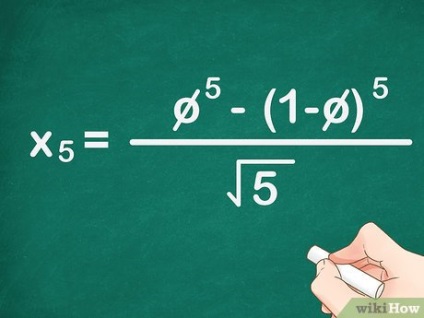
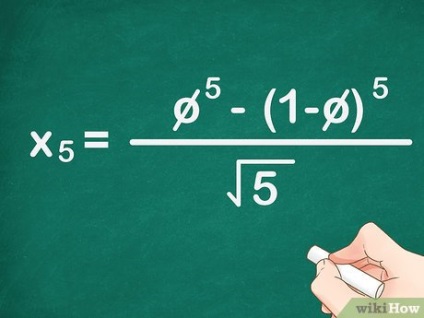
• Наприклад, якщо потрібно знайти п'яте число послідовності, в формулу підставте 5. Формула запишеться так: x 5> = φ 5 - (1 - φ) 5 5 - (1 \ phi) ^ >>>>.

У формулу підставте золотий перетин. Золотий перетин приблизно дорівнює 1,618034; підставте в формулу це число. [5]

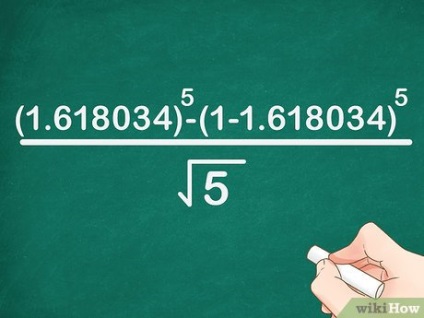
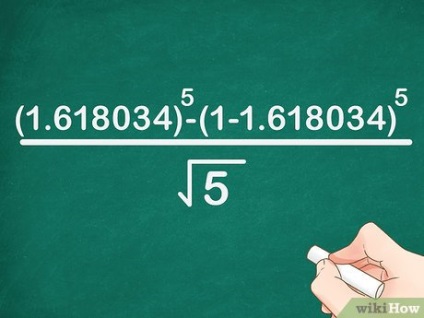
• Наприклад, якщо потрібно знайти п'яте число послідовності, формула запишеться так: x 5> = (1. 618034) 5 - (1 - 1. 618034) 5 5 - (1-1,618034) ^ >>>>.

Обчисліть вираз в дужках. Не забувайте про правильний порядок виконання математичних операцій, в якому вираз в дужках обчислюється в першу чергу: 1 - 1. 618034 = - 0. 618034.

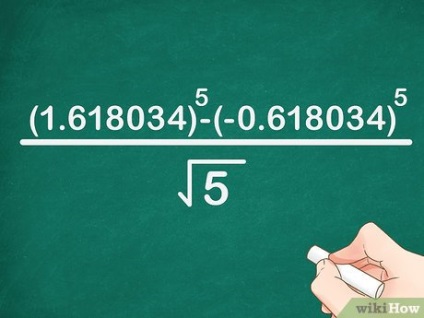
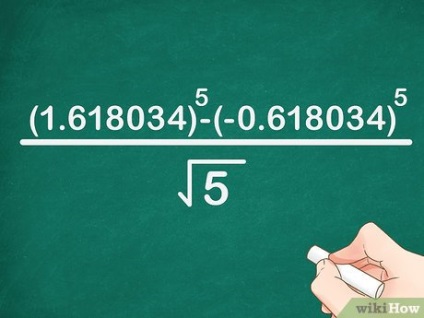
• У нашому прикладі формула запишеться так: x 5> = (1. 618034) 5 - (- 0. 618034) 5 5 - (- 0,618034) ^ >>>>.

Зведіть числа в ступені. Зведіть до відповідних ступеня два числа, які знаходяться в чисельнику.

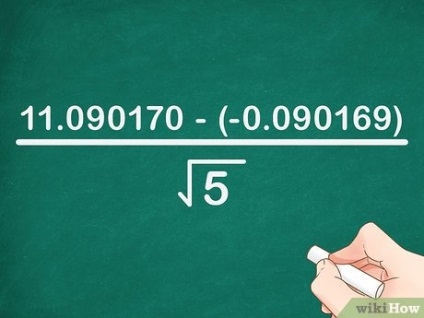
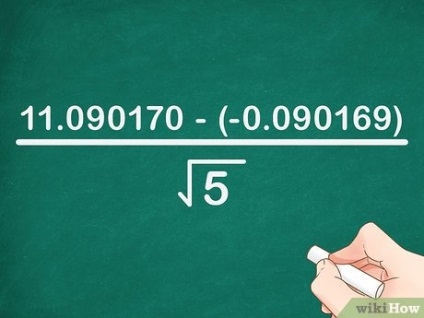
• У нашому прикладі: 1. 618034 5 = 11. 090170 = 11,090170>; - 0. 618034 5 = - 0. 090169 = -0,090169>. Формула запишеться так: x 5 = 11. 090170 - (- 0. 090169) 5 = >>>.

Відніміть два числа. Перед тим як приступити до поділу, відніміть числа, які знаходяться в чисельнику.

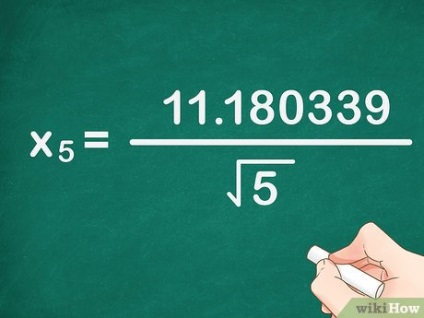
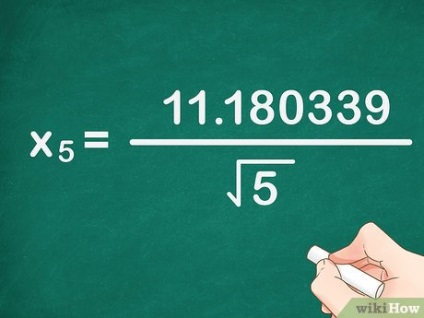
• У нашому прикладі: 11. 090170 - (- 0. 090169) = 11. 180339. Формула запишеться так: x 5> = 11. 180339 5 >>>.

Отриманий результат розділіть на квадратний корінь з 5. Квадратний корінь з 5 приблизно дорівнює 2,236067.

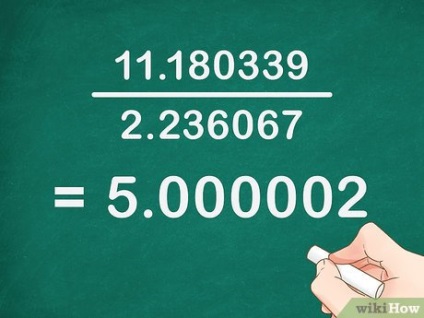
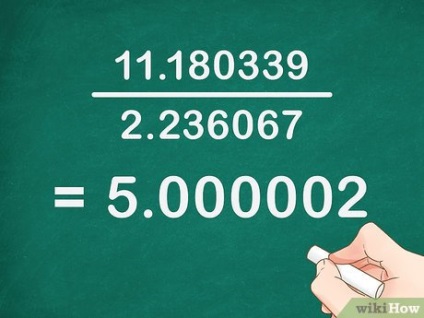
• У нашому прикладі: 11. 180339 2. 236067 = 5. 000002> = 5,000002>.

Отриманий результат округлите до найближчого цілого числа. Останній результат буде десятковим дробом, яка близька до цілого числа. Таке ціле число являє собою число послідовності Фібоначчі.

• Якщо в обчисленнях використовувати неокругленние числа, ви отримаєте ціле число. Працювати з округленими числами набагато легше, але в цьому випадку ви отримаєте десяткову дріб. [6]
• У нашому прикладі ви отримали десяткову дріб 5,000002. Округлите її до найближчого цілого числа і отримаєте п'яте число послідовності Фібоначчі, що дорівнює 5.

Схожі статті

• C ряд чисел Фібоначчі такі різні рішення

• Установка лазерної трубки послідовність операцій

• Терміни і послідовність прорізування зубів у дітей зі схемою і таблицею