Дробу і їх скорочення - ще одна тема, яка починається в 5 класі. Тут формується база цієї дії, а потім ці вміння тягнуться ниточкою в вищу математику. Якщо учень не засвоїв, як скорочувати дроби, то у нього можуть виникнути проблеми в алгебрі. Тому краще усвідомити кілька правил раз і назавжди. А ще запам'ятати один заборона і ніколи його не порушувати.
Дріб і її скорочення
Що це таке, знає кожен учень. Будь-які дві цифри розташовані між горизонтальною лінією відразу сприймаються, як дріб. Однак не всі розуміють, що нею може стати будь-яке число. Якщо воно ціле, то його завжди можна розділити на одиницю, тоді вийде неправильна дріб. Але про це пізніше.
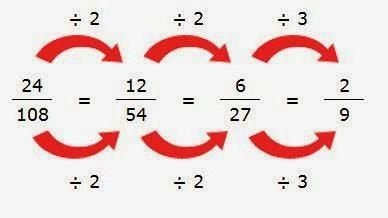
Початок завжди просте. Спочатку потрібно з'ясувати, як скоротити правильну дріб. Тобто таку, у якій чисельник менше, ніж знаменник. Для цього буде потрібно згадати основну властивість дробу. Воно стверджує, що при множенні (так само, як і розподілі) одночасно її чисельника і знаменника на однакове число виходить, рівноцінна вихідної дріб.
Дії ділення, які виконуються в цій властивості і призводять до скорочення. Тобто максимальному її спрощення. Дріб можна скорочувати до тих пір, поки над рисою і під нею є загальні множники. Коли їх вже не буде, то скорочення неможливо. І кажуть, що ця дріб нескоротний.
два способи
1. Покрокове скорочення. У ньому використовується метод прикидки, коли обидва числа діляться на мінімальний загальний множник, який зауважив учень. Якщо після першого скорочення видно, що це не кінець, то розподіл триває. Поки дріб не стане нескоротного.
2. Знаходження найбільшого загального дільника у чисельника і знаменника. Це найраціональніший спосіб того, як скорочувати дроби. Він має на увазі розкладання чисельника і знаменника на прості множники. Серед них потім потрібно вибрати всі однакові. Їх твір дасть найбільший спільний множник, на який скорочується дріб.

Обидва ці способу рівноцінні. Учневі пропонується освоїти їх і користуватися тим, який більше сподобався.
Що робити, якщо є букви і дії додавання і віднімання?
З першою частиною питання все більш-менш зрозуміло. Букви можна скорочувати так само як і числа. Головне, щоб вони виступали в ролі множників. А ось з другої у багатьох виникають проблеми.
Важливо запам'ятати! Скорочувати можна тільки числа, які є множниками. Якщо вони складові - не можна.
Для того щоб зрозуміти, як скорочувати дроби, що мають вид алгебраїчного виразу, потрібно засвоїти правило. Спочатку уявити чисельник і знаменник у вигляді твору. Потім можна скорочувати, якщо з'явилися загальні множники. Для подання у вигляді множників знадобляться такі прийоми:
- угруповання;
- винесення за дужки;
- застосування тотожностей скороченого множення.
Причому останній спосіб дає можливість відразу отримати складові у вигляді множників. Тому його необхідно використовувати завжди, якщо видно відома закономірність.
Але це ще не страшно, потім з'являються завдання зі ступенями і корінням. Ось тоді потрібно набратися сміливості і засвоїти пару нових правил.
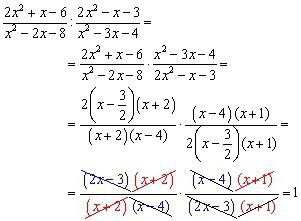
Вираз зі ступенем
Дріб. У чисельнику і знаменнику твір. Є букви і числа. А вони ще й зведені в ступінь, яка теж складається з доданків або множників. Є чого злякатися.
Для того щоб розібратися в тому, як скорочувати дроби зі ступенями, потрібно вивчити два моменти:
- якщо в показнику ступеня стоїть сума, то її можна розкласти на множники, ступенями яких будуть вихідні складові;
- якщо різниця, то на ділене і дільник, у першого в мірою зменшуване, у другого - від'ємник.
Після виконання цих дій стають видні загальні множники. У таких прикладах немає необхідності обчислювати все ступеня. Досить просто скоротити ступеня з однаковими показниками і підставами.
Для того щоб остаточно засвоїти те, як скорочувати дроби зі ступенями, потрібно багато практикуватися. Після декількох однотипних прикладів дії будуть виконуватися вже автоматично.
А якщо у виразі варто корінь?
Його теж можна скоротити. Тільки знову ж, дотримуючись правил. Причому вірні всі ті, які були описані вище. Загалом, якщо стоїть питання про те, як скоротити дріб з корінням, то потрібно ділити.
На ірраціональні вирази теж можна розділити. Тобто якщо в чисельнику і знаменнику стоять однакові множники, укладені під знак кореня, то їх можна сміливо скорочувати. Це призведе до спрощення виразу і виконання завдання.
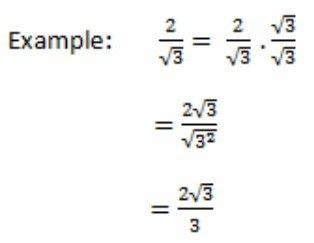
Якщо після скорочення під рискою дробу залишилася ірраціональність, то від неї потрібно позбутися. Іншими словами, помножити на неї чисельник і знаменник. Якщо після цієї операції з'явилися загальні множники, то їх знову потрібно буде скоротити.
Ось, мабуть, і все про те, як скорочувати дроби. Правил небагато, а заборона один. Ніколи не скорочувати складові!