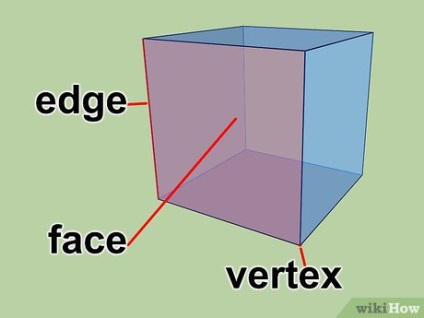
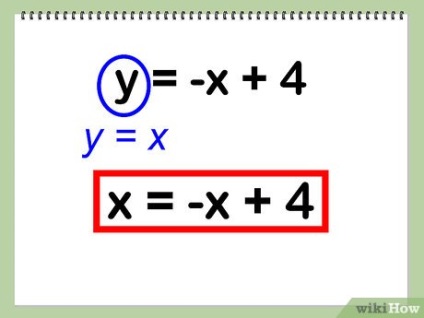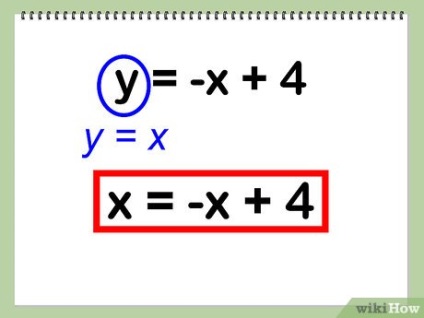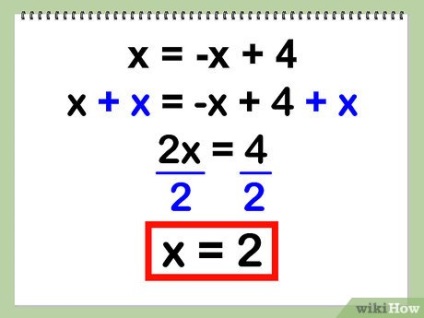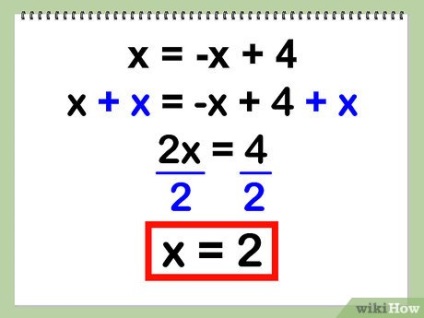Теорема Ейлера. Теорема стверджує, що в будь-якому многограннике число його вершин плюс число його граней мінус число його ребер завжди дорівнює двом. [1]
- Формула, що описує теорему Ейлера: F + V - E = 2
- F - число граней.
- V - число вершин.
- E - число ребер.
Перепишіть формулу, щоб знайти число вершин. Якщо вам дано число граней і число ребер багатогранника, ви можете швидко знайти число його вершин за допомогою формули Ейлера.
Підставте дані вам значення в цю формулу. В результаті ви отримаєте число вершин багатогранника.
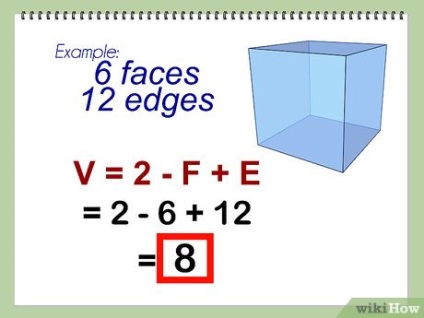
- Приклад: знайдіть число вершин багатогранника, у якого 6 граней і 12 ребер.
- V = 2 - F + E
- V = 2 - 6 + 12
- V = -4 + 12
- V = 8
Метод 2 з 5:
Пошук вершини області системи лінійних нерівностей [2] Правити
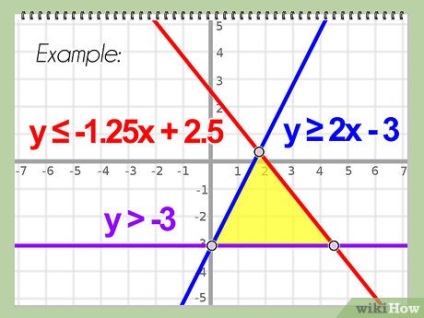
Побудуйте графік вирішення (області) системи лінійних нерівностей. У певних випадках на графіку можна побачити деякі або всі вершини області системи лінійних нерівностей. В іншому випадку вам доведеться знайти вершину алгебраїчно.
- При використанні графічного калькулятора ви можете подивитися весь графік і знайти координати вершин.
Перетворіть нерівності в рівняння. Для того, щоб вирішити систему нерівностей (тобто знайти «х» і «у»), вам необхідно замість знаків нерівності поставити знак «дорівнює».
- Приклад: дана система нерівностей:
- Перетворіть нерівності в рівняння:
Тепер висловіть будь-яку змінну в одному рівнянні і підставте її в інше рівняння. У нашому прикладі підставте значення «у» з першого рівняння в друге рівняння.
- приклад:
- Підставляємо у = х в у = - х + 4:
Знайдіть одну із змінних. Зараз у вас є рівняння тільки з однією змінною «х», яку легко знайти.
- Приклад: х = - х + 4
- х + х = 4
- 2x = 4
- 2x / 2 = 4/2
- х = 2
Знайдіть іншу змінну. Підставте знайдене значення «х» в будь-який з рівнянь і знайдіть значення «у».
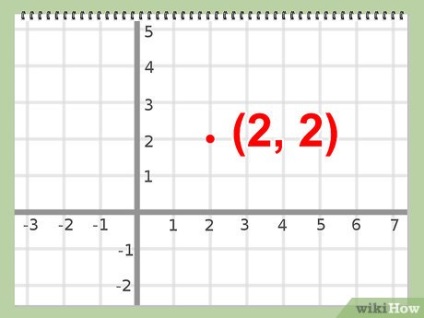
Знайдіть вершину. Вершина має координати, рівні знайденим значенням «х» і «у».
- Приклад: вершина області даної системи нерівностей є точка О (2,2).
Метод 3 з 5:
Пошук вершини параболи через вісь симетрії Правити
Розкладіть рівняння на множники. Є кілька способів розкладання квадратного рівняння на множники. В результаті розкладання ви отримуєте два двочлена, які при перемножуванні приведуть до вихідного рівняння.
- Приклад: дано квадратне рівняння
- 3x2 - 6x - 45
- Спочатку винесіть за дужки загальний множник: 3 (x2 - 2x - 15)
- Перемножте коефіцієнти «а» і «с»: 1 * (-15) = -15.
- Знайдіть два числа, результат множення яких дорівнює -15, а їх сума дорівнює коефіцієнту «b» (b = -2): 3 * (-5) = -15; 3 - 5 = -2.
- Підставте знайдені значення в рівняння ax2 + kx + hx + c: 3 (x2 + 3x - 5x - 15).
- Розкладіть вихідне рівняння: f (x) = 3 * (x + 3) * (x - 5)
Знайдіть точку (точки), в якій графік функції (в даному випадку парабола) перетинає вісь абсцис. [3] Графік перетинає вісь Х при f (x) = 0.
- Приклад: 3 * (x + 3) * (x - 5) = 0
- х +3 = 0
- х - 5 = 0
- х = -3; х = 5
- Таким чином, коріння рівняння (або точки перетину з віссю Х): А (-3, 0) і В (5, 0)
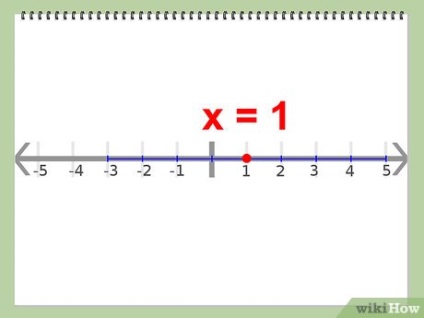
Знайдіть вісь симетрії. Вісь симетрії функції проходить через точку, що лежить посередині між двома країнами. При цьому вершина лежить на осі симетрії.
- Приклад: х = 1; це значення лежить посередині між -3 і +5.
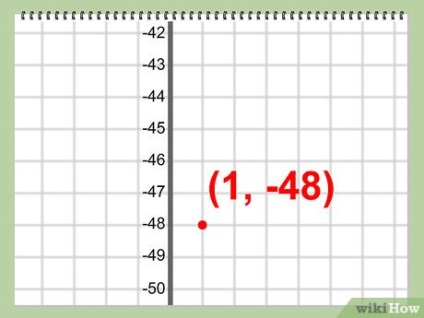
Підставте значення «х» в вихідне рівняння і знайдіть значення «у». Ці значення «х» і «у» - координати вершини параболи.
- Приклад: у = 3x2 - 6x - 45 = 3 (1) 2 - 6 (1) - 45 = -48
Запишіть відповідь.
- Приклад: вершина даного квадратного рівняння є точка О (1, -48)
Схожі статті