1.Поняття комплексного числа.
Вираз виду z = x + iy називається комплексним числом.
Число х називається дійсною частиною комплексного числа z і позначається Re (z), число y - уявною частиною комплексного числа z і позначається Im (z). Числа z = x + iy і z1 = x - iy називаються сполученими. Якщо рівні дійсні та уявні частини комплексного числа, то вони називаються рівними тобто z1 = z2 або x1 + iy1 = x2 + iy2.
Операції над комплексними числами.
1. Сума (різниця) комплексних чисел.
z 1 + z 2 = x 1 + x 2 + i (y 1 + y 2).
2. Твір комплексних чисел.
z 1 z 2 = (x 1 x 2 - y 1 y 2) + i (x 1 y 2 + x 2 y 1).
i² = (0 + i1) (0 + i1) = (0 -1) + i (0 + 0) = -1.
3. Розподіл двох комплексних чисел.

Розглянемо на площині декартову прямокутну систему координат Oxy.
Кожному комплексному числу Z = x + iy ставиться у відповідність єдина точка площини z (xy). Площина Oxy, де кожна точка ототожнена з комплексним числом, називається комплексною.
Координатні осі Ox і Oy, на яких розташовані дійсні та уявні числа, називаються дійсної та уявної осями.
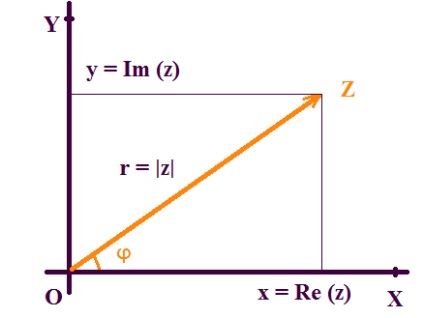
2.Трігонометріческая форма комплексного числа.
До будь-якої точки комплексної площини з початку координат можна провести вектор певної довжини r. Число r називається модулем комплексного числа z і позначається | z |.