Завантажити замітку в форматі Word. приклади в форматі Excel [1]
Коротенько. Контрольна карта використовується для графічного відображення інформації про досліджуваному параметрі процесу. На контрольній карті наносять експериментально виміряні значення, а також лінію середнього, верхню і нижню межі (середнє ± 3 сигми). Якщо процес статистично керований, тобто відхилення точок від середнього пов'язано лише з природною варіабельністю властивою процесу, то всі точки лежать між кордонами. В цьому випадку для зменшення варіабельності (ширини коридору між кордонами) та / або середнього значення необхідні зусилля, спрямовані на вдосконалення процесу. Якщо процес характеризується відсутністю керованості, тобто деякі точки виходять за контрольні кордону, зусилля повинні бути спрямовані на виявлення особливих причин варіабельності і їх усунення. Приклади особливих причин варіабельності: погано навчені виконавці, бракована партія комплектуючих, знос обробного верстата, поломка автомобіля і ін. Ще раз підкреслю, контрольна карта показує, якого роду рішення повинен прийняти менеджер: удосконалювати процес або знайти і виключити особливі причини.
Таким чином, одне із завдань контрольної карти Шухарта - виявлення ситуацій, які свідчать про відсутність статистичної керованості процесом.
І ось недавно мене осінило! Так адже всі ці критерії, схоже, відповідають одній і тій же ймовірності зазначених подій! Давайте перевіримо.
Критерій 1. Вихід однієї точки за 3-сігмовие межі вказує на відсутність керованості
Про що йде мова? На рис. 1 зображено 100 значень випадково величини, одна з яких вийшло за межі 3-сігмовой кордону. На малюнок також нанесені лінія середнього та 3-сігмовие кордону.
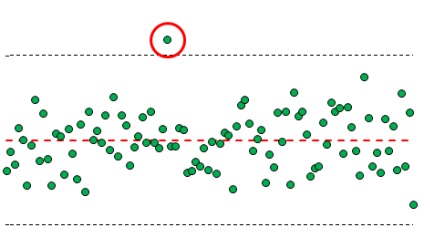
Мал. 1. Приклад виходу точки за 3-сігмовие кордону
За допомогою функції = НОРМСТРАСП (див. Також однойменний лист Excel-файлу) побудуємо табличку залежності ймовірності виходу випадкової величини за n -сігмовую округу від середнього (рис. 2) і представимо інтегральну ймовірність розподілу випадкової величини графічно (рис. 3).
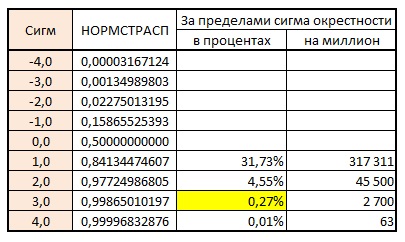
Мал. 2. Ймовірність виходу за 3-сігмовую околиця
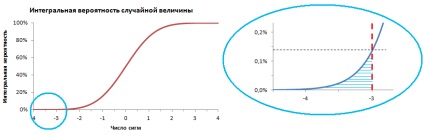
Мал. 3. Інтегральна ймовірність розподілу випадкової величини
Релевантність першого критерію становить 99,73%. Тобто тільки з ймовірністю 0,27% вихід за межі 3-сігмовой кордони не буде пов'язаний зі спеціальними причинами, а буде обумовлений «викидом» випадкової (статистично керованої) величини - помилкова тривога.
Для моделювання поведінки випадкової нормально розподіленої величини скористаємося функцією Excel = НОРМСТОБР (СЛЧИС ()) (див. Лист «Вихідний). Контрольна карта процесу моделювання зображена на рис. 4.
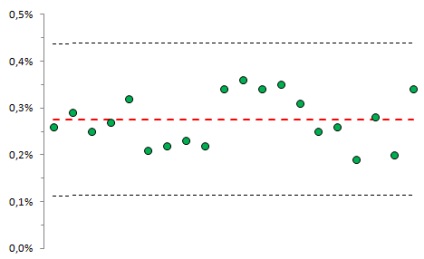
Мал. 4. Ймовірність виходу за 3-сігмовие кордону
На рис. 4 по осі абсцис - номер серії (кожна з 10 000 значень); по осі ординат - ймовірність виходу значення за межі 3 сигм. Для даної контрольної карти середнє = 0,28%, що цілком відповідає теоретичним 0,27%. Якщо в Excel-файлі натискати F9, то карта на очах будемо трохи змінюватися.
Критерій 2. Вихід хоча б двох з трьох послідовних точок, що лежать по одну сторону від центральної лінії, за 2-сігмовие межі вказує на відсутність керованості
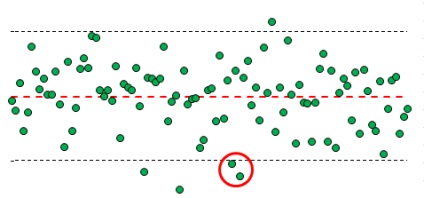
Мал. 5. Приклад виходу хоча б двох з трьох послідовних точок, що лежать по одну сторону від центральної лінії, за 2-сігмовие межі
Звернемося ще раз до таблиці на рис. 2. Ймовірність виходу випадкової величини за межі 2-сігмовой околиці становить 4,55%. Ймовірність виходу тільки по одну зі сторін від середнього (вище або нижче) становить 4,55 / 2 = 2,275%. Ймовірність виходу за межі 2-сігмовой околиці по одну сторону від середнього двох точок поспіль [2] = (4,55 * 2,275%) = 0,104%. Якщо взяти будь-які три точки, то за межі 2-сігмовой околиці можуть вийти, або дві точки поспіль, або дві точки через одну. Таким чином, ймовірність того, що хоча б дві з трьох послідовних точок, що лежать по одну сторону від центральної лінії, вийдуть за 2-сігмовие межі, складає = 0,104 * 2 = 0,207%.
Результати моделювання наведені на рис. 6.
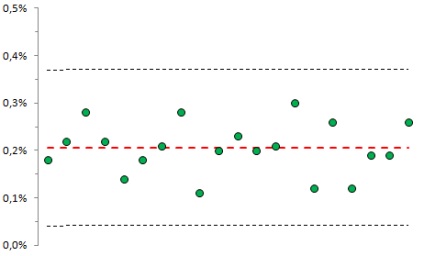
Мал. 6. Імовірність серії з двох точок з трьох послідовних за межами 2-сігмових кордонів
На рис. 6 по осі абсцис - 20 серій (кожна з 10 000 значень); по осі ординат - ймовірність виходу хоча б двох з трьох послідовних точок, що лежать по одну сторону від центральної лінії, за 2-сігмовие межі. Для даної контрольної карти середнє = 0,205%, що цілком відповідає теоретичним 0,207%.
Релевантність другого критерію, що вказує на відсутність керованості, трохи вище, ніж для першого критерію, і становить 99,79%. Тобто, з ймовірністю 0,207% вихід за межі 2-сігмовой кордону хоча б двох з трьох послідовних точок не буде пов'язаний зі спеціальними причинами, а буде обумовлений «викидом» випадкової (статистично керованої) величини.
Критерій 3. Вихід, щонайменше, 4 з 5 послідовних точок, що лежать по одну сторону від центральної лінії, за 1-сігмовие межі вказує на відсутність керованості
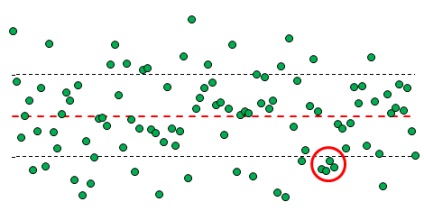
Мал. 7. Серія чотирьох точок з п'яти послідовних за межами 1-сігмовой кордону
Спроба розрахувати теоретичну ймовірність такого події на основі таблиці (рис. 2) мені не вдалася. L Легко побачити, що ймовірність виходу випадкової величини за межі 1-сігмовой кордону = 31,731%. Ймовірність виходу за межі 1-сігмовой околиці по одну сторону від середнього чотирьох точок поспіль = 31,731 * (15,866%) 3 = 0,127%. А ось як розрахувати вихід, по крайней мере. чотирьох з п'яти послідовних точок за межі 1-сігмовой околиці, мені не зрозуміло ... Особливо з огляду на, що треба взяти до уваги і більш складні випадки, коли серія може включати п'ять, шість і більше точок ...
Тому залишилося звернутися до моделювання (рис. 8).
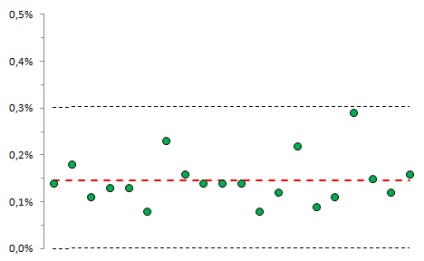
Мал. 8. Імовірність появи серії, в якій, по крайней мере, чотири точки з п'яти послідовних, виходять за межі 1-сігмових кордонів
Імовірність таких серій на рівні 0,15%.
Критерій 4. Розташування, щонайменше, 8 послідовних точок по одну сторону від центральної лінії вказує на відсутність керованості

Мал. 9. Серія з восьми послідовних точок по одну сторону від центральної лінії
Імовірність того, що випадкова величина вісім разів поспіль прийме значення по одну сторону від середнього, становить (1/2) 8 = 0,391%. Моделювання непогано це підтверджує (рис. 10)
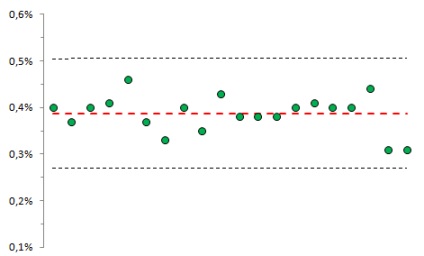
Мал. 10. Імовірність появи серії з восьми послідовних точок по одну сторону від центральної лінії
На рис. 10 по осі абсцис - 20 серій (кожна з 10 000 значень); по осі ординат - ймовірність появи, щонайменше, восьми послідовних точок по одну сторону від центральної лінії. Для даної контрольної карти середнє = 0,387%.
Зведемо отримані дані в єдину таблицю