Мал. 2. Умовна ентропія
3. Спільна ентропія - середня кількість інформації на пару пе-Реда і прийнятих символів (рис. 3).
H (X, Y) = H (Y, X) = H (X) + H (Y / X) = H (Y) + H (X / Y) = H (X) + H (Y) -H ( X × Y).
4. Взаємна ентропія - ентропія спільного появи статистично-залежних повідомлень (рис. 4).
Мал. 3 Спільна ентропія
Мал. 4. Взаємна ентропія
На практиці найчастіше зустрічаються взаємозалежні символи і повідомлення. Наприклад, при передачі текстових повідомлень передаються не просто букви, а слова, що мають певні смислові значення. При цьому, кожна буква, і поєднання букв мають різні ймовірності появи в тексті. Умовна ентропія враховує взаємозв'язок подій через їх умовні ймовірності.
Розглянемо схему рис. 5:
Мал. 5. Передача повідомлень
Джерело повідомлень X - виробляє повідомлення, елементами якого є символи алфавіту джерела. ймовірності появи на виході яких дорівнюють p (x1), p (x2). p (xm), при цьому:
Ентропія джерела являє собою невизначеність появи на виході джерела повідомлень символу первинного алфавіту і визначається співвідношенням:
()
Приймач повідомлень Y - приймає повідомлення, елементами якого є символи алфавіту приймача. ймовірності появи на вході яких дорівнюють p (y1), p (y2). p (ym), при цьому:
Ентропія приймача являє собою невизначеність появи на вході приймача повідомлень символу після його появи на виході джерела і визначається співвідношенням:
Якщо в каналі зв'язку відсутні втрати інформації (немає перешкод, ис-каженій і т. Д.), То символу xi відповідає символ yi. В іншому випадку xi може бути прийнятий як будь-який з можливих y1, y2. ym. з відповідними можливостями.
При відсутності втрат: H (X) = H (Y). При наявності перешкод вони знищити-жают частина інформації. При цьому втрати інформації можна визначити через приватні і загальну умовну ентропію.
Обчислення загальної умовної ентропії зручно проводити за допомогою канальних матриць (матрицею перехідних станів).
Втрати інформації в каналі можна оцінювати з боку джерела або приймача повідомлень.
Розглянемо порядок визначення втрат з боку джерела (відомий передається сигнал). При цьому, умовна ймовірність p (yj / xi) означає ймовірність того, що при передачі повідомлення xi отримано повідомлення yj. Канальна матриця має вигляд, наведений в табл. 1.
Ймовірності розташування на діагоналі характеризує ймовірність правильної передачі, інші - помилковою. Для рівноймовірно сигналів на вході приймача загальна умовна ентропія обчислюється за формулою:
Для НЕ рівноймовірно сигналів на вході приймача загальна умовна ентропія обчислюється за формулою:
Приватна умовна ентропія, що визначає втрати, що припадають на частку сигналу y1. дорівнює:
Приклад 1. Обчислити ентропію джерела повідомлень, видає два символи 0 і 1 з ймовірностями p (0) = 3/4, p () = 1/4 і умовними ймовірностями: p (0/0) = 2/3, p (/ 0) = 1/3, p (0/1) = 1, p (/ 1) = 0. т. е. після 1 завжди йде 0.
Рішення: Для випадку взаємозалежних, що не рівно можливих елементів ентропія дорівнює:

Приклад 2. Визначити ентропію джерела повідомлень, якщо імовірність-ності появ символів на вході приймача, рівні: P (b1) = 0,1; P (b2) = 0,3; P (b3) = 0,4, P (b4) = 0,2 а канальна матриця має вигляд:
Сума ймовірності при однойменних умовах дорівнює
Рішення: Визначимо ентропію джерела
.
= 0,1 × 0,01 + 0,3 × 0,98 + 0,4 × 0,01 + 0, × 2 × 0,01 = 0,301;
0,1 × 0 + 0,3 × 0 + 0,4 × 0,98 + 0,2 × 0,02 = 0,396;
0,1 × 0 + 0,3 × 0 + 0,4 × 0,01 + 0,2 × 0,97 = 0,198;
При цьому ентропія джерела дорівнює:
Приклад 3. Визначити ентропію джерела і умовну ентропію повідомлень, переданих по каналу зв'язку, і складаються з рівноймовірно символів, якщо вплив перешкод в каналі описується матрицею:
.
Рішення: Для рівноймовірно символів в повідомленні ентропія джерела повідомлень дорівнює:
Повна умовна ентропія дорівнює:
=
Приклад 4. Визначити ентропію приймача повідомлень, якщо ймовірності появи символів a1, a2 і a3 на вході джерела повідомлень рівні P (a1) = 0,5; P (a2) = 0,3 і P (a3) = 0,2, а канальна матриця має вигляд:
,
Рішення: Ентропія приймача дорівнює:
.
Ймовірності появи символів на вході приймача
;
;
.
.
2. ЕНТРОПІЯ ДЖЕРЕЛА БЕЗПЕРЕРВНИХ ПОВІДОМЛЕНЬ
Для опису інформаційних властивостей безперервного джерела (сигналу) використовується поняття диференціальної ентропії. Для її отримання скористаємося формулою для ентропії дискретних повідомлень. Відповідно до графіка функції щільності ймовірності (рис. 6.) можна записати p (xi) = ?. Де p (xi) - імовірність того, що x лежить в межах i -го кроку квантування.
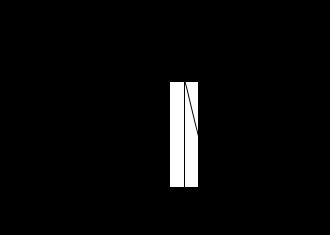
Мал. 6. Графік функції щільності ймовірності
При цьому, вираз для ентропії можна представити у вигляді
Переходимо до межі:
.
Повна ентропія джерела безперервних повідомлень складається з двох доданків, одне з яких визначається законом розподілу, а друге є постійною величиною, що визначає крок квантування, який впливає на точність вимірювань. Цей член виразу визначає постійну складову і виключається з розгляду.
Значення першого доданка визначається законом розподілу і характеризує диференціальну ентропію безперервного джерела (т. К. F (x) - щільність ймовірності або диференційний закон розподілу)
Диференціальна ентропія - частина ентропії джерела безперервних повідомлень, яка залежить від щільності ймовірності сигналу x (t). що видається джерелом.
Різні класи фізичних явищ і процесів підпорядковуються різним законам розподілу. Безперервні сигнали повністю характеризуються законами розподілу (інтегральним або диференціальним). На будь-які реальні сигнали накладаються певні обмеження, наприклад: по середньої потужності (нагрів апаратури); по миттєвої або пікової потужності (перевантаження).
Так як диференціальна ентропія залежить від щільності ймовірності, визначимо, для якого закону вона максимальна. Т. е. При якому розподілі ймовірності, сигнал заданої потужності має максимальну ентропію. Для знаходження максимального значення ентропії необхідно скористатися варіаційної теоремою з використанням невизначених множників Лагранжа за умов нормування і незмінності середнього квадрата:
; .
Вирішивши рівняння, отримаємо симетричний нормальний закон розподілу
Якщо середню потужність не обмежувати
то отримаємо рівномірний закон розподілу.
Визначимо диференціальну ентропію для нормального розподілу, т. Е. Сигналу з обмеженою середньою потужністю. Отримане в результаті рішення варіаційної задачі нормальний розподіл є симетричним. Якщо в інтегралі для диференціальної ентропії зробити заміну x = y-mx. то інтеграл не зміниться, а значить, ентропія не залежить від математичного очікування і дорівнює ентропії центрованої випадкової величини.
Визначимо максимальне значення для ентропії:
Диференціальна ентропія для нормального розподілу дорівнює:
Повна ентропія для нормального розподілу дорівнює:
Якщо врахувати що h (x) - це математичне сподівання функції [-log2 f (x)] від випадкової величини x з щільністю f (x), то можна записати.

Відповідно до центральною граничною теоремою нормальним законам розподілу підкоряються широкий клас, так званих гауссових випадкових процесів або реальних сигналів.
Білий шум - перешкода з найбільш '' шкідливими "властивостями. Т. Е. Передає максимальну кількість шкодять відомостей при заданій середньої потужності і дозволяє спростити розрахунки для найгіршого випадку.
Для того щоб сигнал з обмеженою пікової потужністю мав максимальну інформативність необхідно, щоб він мав рівномірний розподіл (рис. 9). Визначимо диференціальну ентропію для рівномірного розподілу, т. Е. Сигналу з обмеженою пікової потужністю. Якщо P-пікова потужність, то - максимальна амплітуда. Рівняння для диференціальної ентропії з урахуванням обмежень має вигляд:
Диференціальна ентропія для рівномірного розподілу дорівнює:
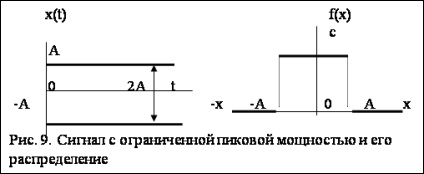
Повна ентропія сигналу з рівномірним розподілом дорівнює:
де m-число рівнів квантування.
Визначимо диференціальну ентропію для експоненціального розподілу. Цей розподіл широко використовується для визначення інтенсивності відмов в радіоелектронній апаратурі
Повна ентропія для експоненціального розподілу дорівнює:
2. Яглом А. М. Яглом І. М. Імовірність і інформація. М. 1957.
3. Шеннон К. Роботи по теорії інформації і кібернетики. - М. Изд. іноз. лит. 1963. - 830 с.
4. Волькенштейн М. В. Ентропія та інформація. - М. Наука, 1986. - 192 с.
5. Цимбал В. П. Теорія інформації та кодування. - М. Вища Школа, 1977. - 288 с.
6. Імовірнісні методи в обчислювальній техніці. / Под ред. А.Н. Лебедєва, Е.А.Чернявского. -М. Вища. шк. 1986.
7. Сєдов Е.А. Взаємозв'язок інформації, енергії і фізичної ентропії в процесах управління та самоорганізації. Інформація та управ-ня. М. Наука, 1986.