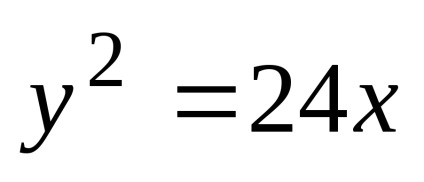Криві другого порядку

Еліпсом називається геометричне місце точок площини, для кожної з яких сума відстаней до двох даних точок цієї площини, які називаються фокусами, є величина постійна і велика, ніж відстань між фокусами.

позначимо

і- фокуси еліпса. нехай- довільна точка еліпса. відрізкиіназиваються фокальними радіусами точки.

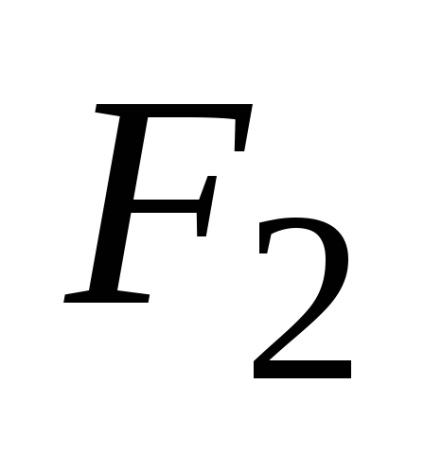
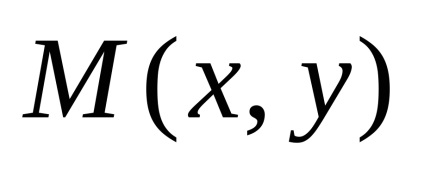
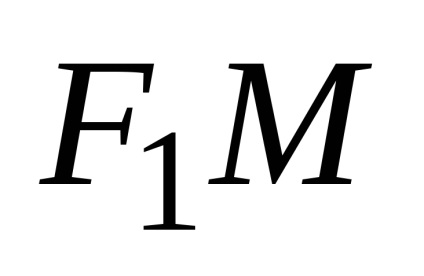
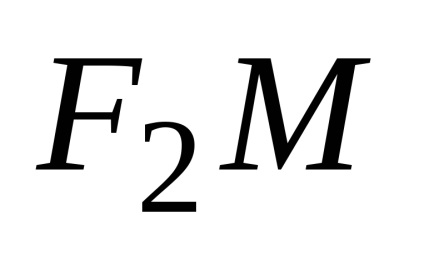
позначимо,

. З визначення еліпса випливає, що, тобто. Так як, то. Отже, знайдемо довжини фокальних радіусові. тоді

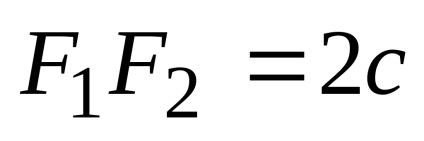
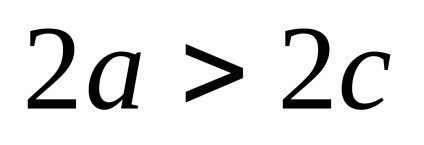
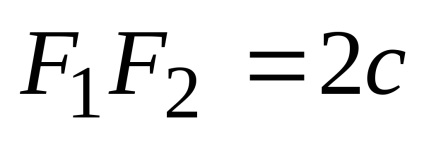
Це рівняння є рівнянням еліпса. Після його перетворень можна отримати більш просте рівняння

,

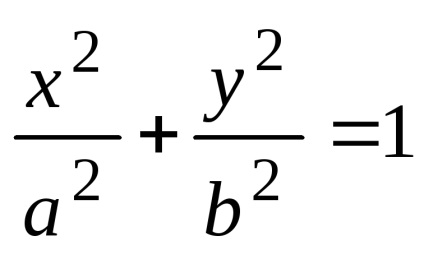
яке називається канонічним рівнянням еліпса. У цьому рівнянні

.

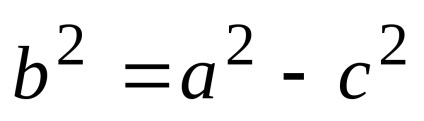
Якщо фокуси еліпса знаходяться на осі Ох. то a> b. В цьому випадку а називається велика піввісь еліпса, а b - малої полуосью. ставлення

називаетсяексцентрісітетомелліпса і характеризує його форму.

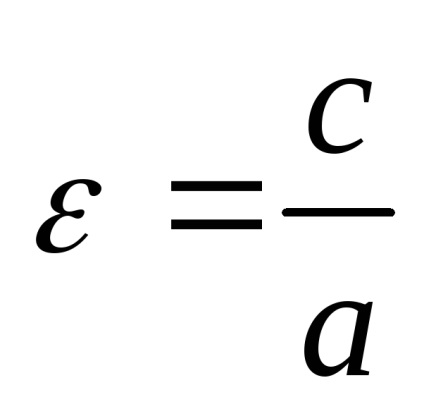
Якщо в рівнянні еліпса b ​​= a. то воно перетворюється в рівняння

, яке є рівнянням кола радіусаа з центром на початку координат.

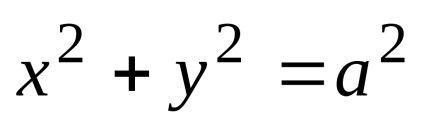
Приклад 1. Скласти рівняння еліпса, велика вісь якого збігається з віссю Ох і дорівнює 10, а відстань між фокусами дорівнює 8.

Рішення . За умовою

. Тоді. Канонічне рівняння еліпса має вигляд.

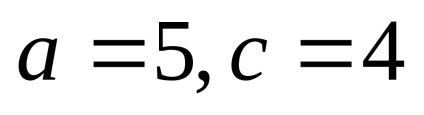
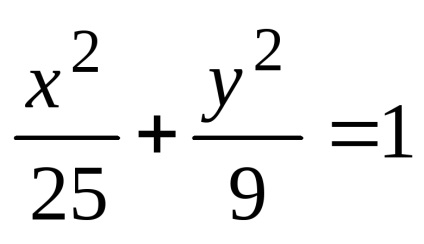
Гіперболою називається геометричне місце точок площини, для кожної з яких абсолютне значення різниці відстаней до двох даних точок цієї площини, які називаються фокусами, є величина постійна і менша, ніж відстань між фокусами.

позначимо

і- фокуси гіперболи. нехай- довільна точка гіперболи.

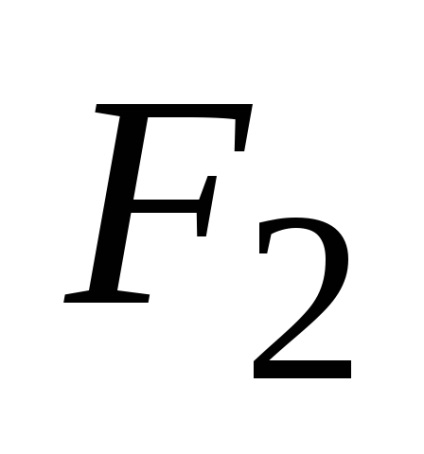
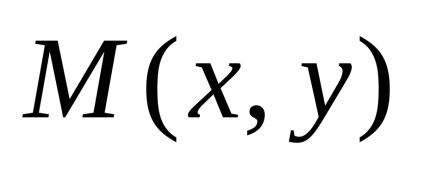
Відстань між фокусами позначимо

, а абсолютне значення різниці відстаней від точки гіперболи до фокусів. Остання рівність можна записати. З визначення гіперболи слід, що, тобто. Так як, то. Отже, можна знайти довжини відстаней від точкидо фокусіві: І. тоді

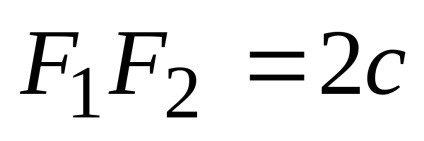
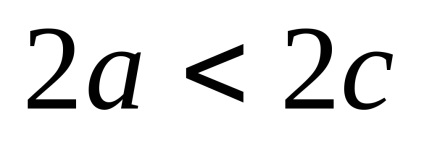
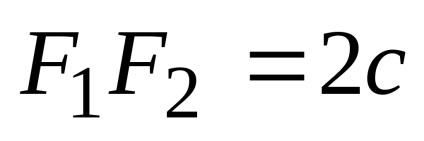
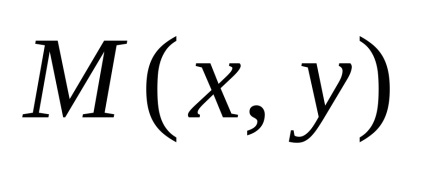
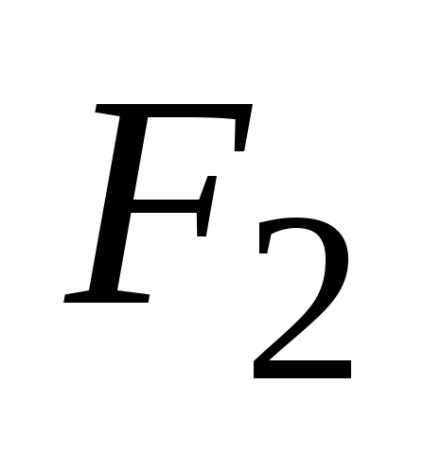
Отримане рівняння є рівнянням гіперболи. Після його перетворень можна отримати більш просте рівняння

,

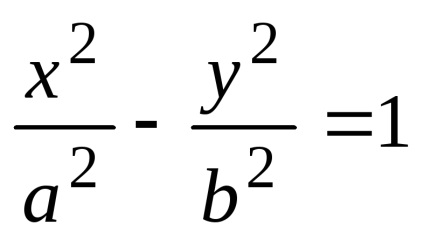
яке називається канонічним рівнянням гіперболи. У цьому рівнянні

.

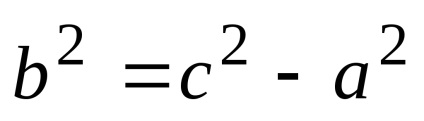
Число а називається дійсною полуосью гіперболи, а число b - мнимої полуосью. рівняння

є уравненіяміасімптот гіперболи. ставлення називаетсяексцентрісітетом гіперболи і характеризує її форму.

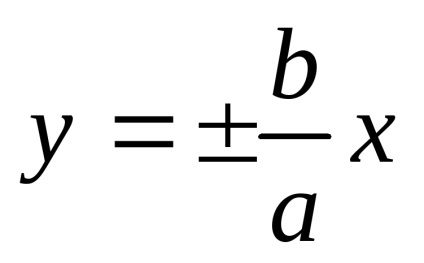
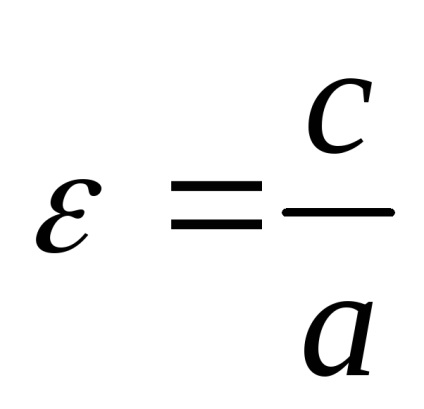
Приклад 2. Дійсна піввісь гіперболи

, ексцентриситет. Скласти канонічне рівняння гіперболи.

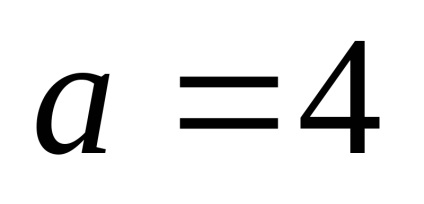
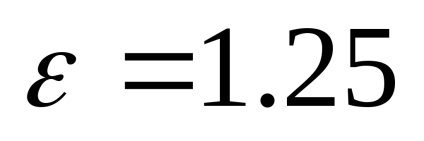
Рішення . Так як ексцентриситет гіперболи

, то ,. Канонічне рівняння гіперболи має вигляд.

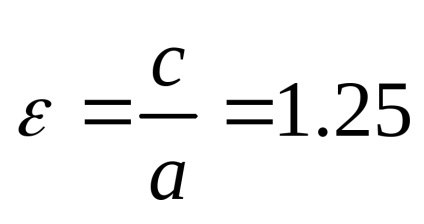
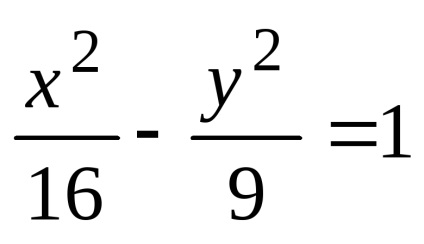
Параболою називається геометричне місце точок площини, для кожної з яких відстань до деякої фіксованої точки площини, яку називають фокусом, дорівнює відстані до деякої фіксованої прямої, званої директоркою.

Позначимо F - фокус, p - відстань від фокуса до директриси. Величина p називається параметром параболи. На параболі візьмемо довільну точку

.

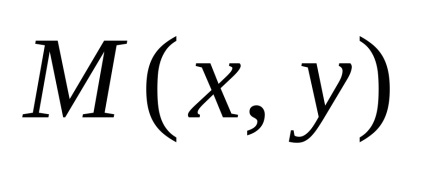
З урахуванням прийнятих позначень можна записати

. Тоді відстань від точкидо фокусуодно, а відстань від точкидо директриси одно. З визначення параболи отримаємо=. Це і є рівняння параболи. Після перетворень можна отримати більш просте рівняння

,

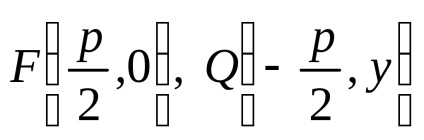
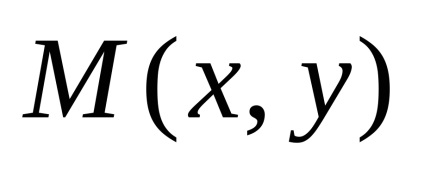
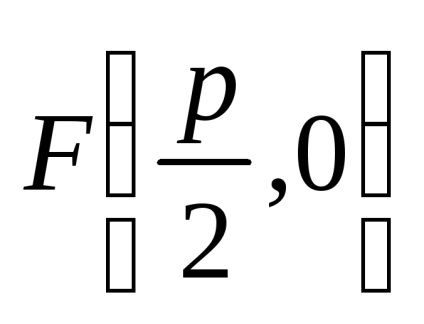
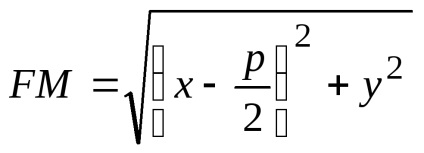
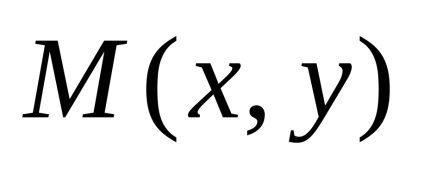
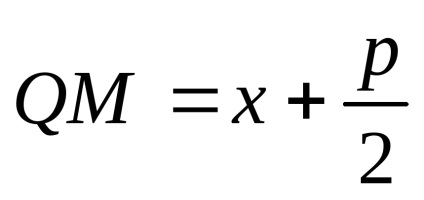
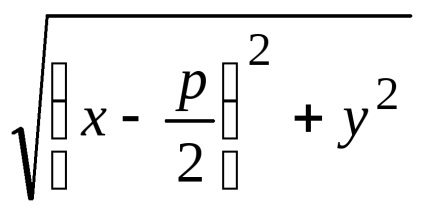
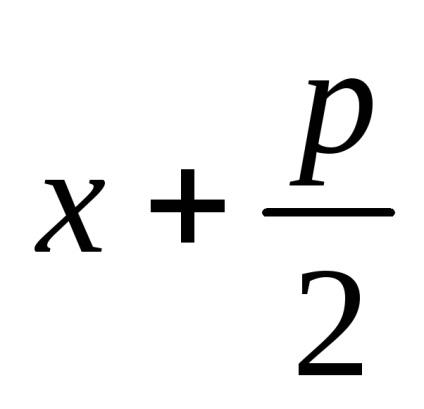
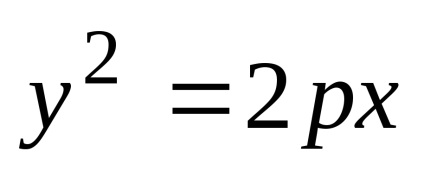
яке називається канонічним рівнянням параболи.

Питання для самоконтролю знань

Що називається еліпсом і як записується його канонічне рівняння?

Що називається ексцентриситетом еліпса і що він характеризує?

Що називається гіперболою і як записується її канонічне рівняння?

Що таке асимптоти гіперболи?

Що називається параболою і як записується її канонічне рівняння?

Завдання для самостійної роботи

Визначити півосі і координати фокусів еліпса

.

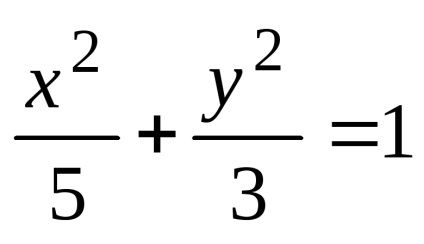
Скласти канонічне рівняння еліпса, у якого велика піввісь дорівнює 5, а ексцентриситет дорівнює 0.6.

Скласти канонічне рівняння гіперболи, якщо її фокуси лежать на осі

і відстань між ними дорівнює 20, а дійсна вісь гіперболи дорівнює 16.

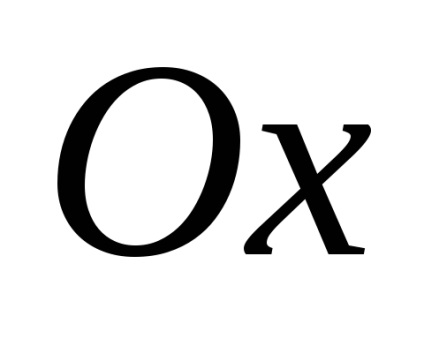
Знайти довжини осей, координати фокусів, ексцентриситет і рівняння асимптот гіперболи.

Знайти рівняння директриси і фокус параболи

.

Схожі статті

• криві лінії

• Криві лінії - студопедія