У творі Квадратура параболи Архімед довів, що площа сегмента параболи, відсікається від неї прямий, складає від площі вписаного в цей сегмент трикутника (див. Малюнок).
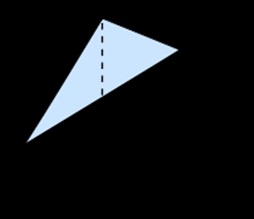
Для доказу Архімед підрахував суму нескінченного ряду:
Кожне складова ряду - це загальна площа трикутників, вписаних в неохоплену попередніми членами ряду частина сегмента параболи.
Крім перерахованого, Архімед обчислив площу поверхні для сегмента кулі і витка відкритої їм «спіралі Архімеда», визначив обсяги сегментів кулі, еліпсоїда, параболоїда і двуполостного гіперболоїда обертання.
Наступне завдання відноситься до геометрії кривих.
Нехай дана деяка крива лінія. Як визначити дотичну в будь-який її точці? Або, якщо перекласти цю проблему на мову фізики, нехай нам відомий шлях деякого тіла в кожен момент часу. Як визначити швидкість його в будь-якій точці?
У школі вчать, як проводити дотичну до кола. Стародавні греки вміли, крім того, знаходити дотичні до еліпса, гіперболи і параболи. Перший загальний метод рішення і цього завдання був знайдений Архімедом. Цей метод згодом ліг в основу диференціального обчислення.
Схема архимедова методу обчислення числа π:
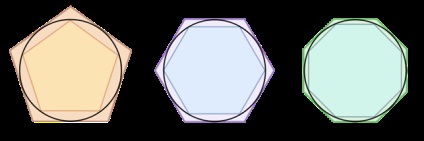
Величезне значення для розвитку математики мало обчислене Архімедом відношення довжини кола до діаметру. У роботі «Про вимір кола» Архімед дав своє знамените наближення для числа π: «архимедова число» 3. Більш того, він зумів оцінити точність цього наближення: 3 <π <3 . Для доказательства он построил для круга вписанный и описанный 96-угольники и вычислил длины их сторон.
В математиці, фізиці і астрономії дуже важливо вміти знаходити найбільші і найменші значення змінних величин - їх екстремуми. Наприклад, як серед циліндрів, вписаних в кулю, знайти циліндр, що має найбільший обсяг? Всі такі завдання в даний час можуть бути вирішені за допомогою диференціального обчислення. Архімед першим побачив зв'язок цих завдань з проблемами визначення дотичних і показав, як вирішувати завдання на екстремуми.
Ідеї Архімеда майже на два тисячоліття випередили свій час. Тільки в XVII столітті вчені змогли продовжити і розвинути праці великого грецького математика.