1.нормальное напруги при розтягуванні і стисненні
2. Визначення поздовжньої і поперечної деформації. закон Гука
3. Статично невизначені завдання
4. Температурні напруги
5. Монтажні напруги
1. Нормальні напруження при розтягуванні і стисненні
Якщо на поверхню призматичного стержня нанести сітку ліній, паралельних і перпендикулярних осі стрижня, і прикласти до нього розтягувальну силу, то можна переконатися в тому, що лінії сітки і після деформації залишаться взаємно перпендикулярними (див. Рис. 1).
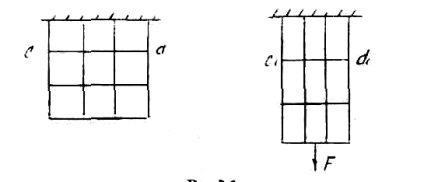
Всі горизонтальні лінії, наприклад, cd перемістяться вниз, залишаючись горизонтальними і прямими. Можна припустити також, що і всередині стрижня буде така ж картина, тобто "Поперечним перерізом стрижня, плоскі і нормальні до його осі до деформації, залишаться плоскими і нормальними до осі і після деформації". Ця важлива гіпотеза носить назву гіпотези плоских перетинів або гіпотези Бернуллі. Формули, отримані на основі цієї гіпотези, підтверджуються результатами дослідів.
Така картина деформацій дає підставу вважати, що в поперечних перетинах діють тільки нормальні напруги, однакові у всіх точках перетину, а дотичні напруження дорівнюють нулю. Якби виникали дотичні напруження, то спостерігалася б кутова деформація, і кути між поздовжніми і поперечними лініями перестали б бути прямими. Якби нормальні напруги різнилися у всіх точках перетину, го там, де напруги вище, була б і більше деформація, а отже, поперечні перерізи не були б плоскими і паралельними. Прийнявши гіпотезу плоских перетинів ми встановлюємо, що.
Оскільки поздовжня сила є рівнодіюча внутрішніх сил
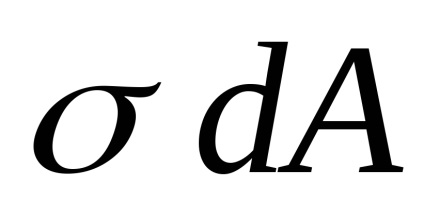
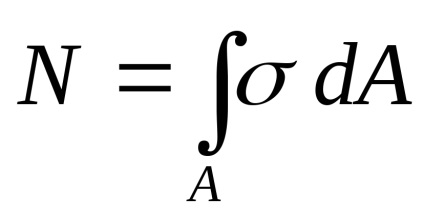
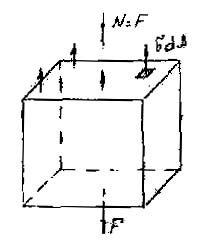
Постійні величини можна виносити за знак інтеграла:
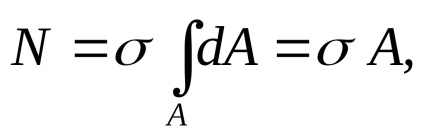
де А площа поперечного перерізу.
Отримуємо формулу для знаходження нормальних напруженішим при розтягуванні або стисненні:
Це одна з найважливіших формул в опорі матеріалів тому її виділимо в рамочки і також будемо поступати надалі.
при розтягуванні

Якщо на брус діє тільки одна зовнішня сила F. то
і напруги можна визначати за формулою:
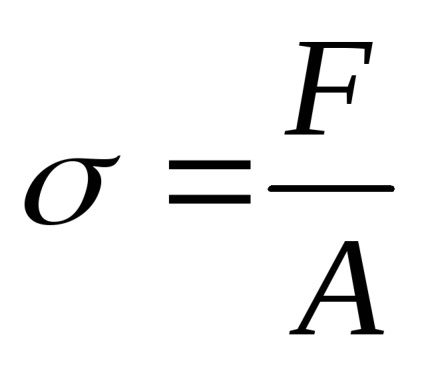
2. Визначення поздовжньої і поперечної деформації
У пружною стадії роботи більшості конструкційних матеріалів напруги і деформації пов'язані прямою залежністю, званої законом Гука:
де Е модуль поздовжньої пружності або модуль Юнга, вимірюється в МПа, характеризує жорсткість матеріалу, тобто здатність чинити опір деформацій, його значення наведені в табліцax довідника;


l первісна довжина, м.
Чим вище значення модуля поздовжньої пружності Е, тим менше деформація. Наприклад, для стали Е = 2,110 5 МПа, а для чавуну Е = (0,75 ... 1,6) 10 5 МПа, тому елемент конструкції з чавуну при однакових інших умовах отримає більшу деформацію, ніж зі сталі. Тут не треба плутати з тим, що доведений до розриву стрижень зі сталі буде мати значно більшу деформацію, ніж чавунний. Мова йде не про граничної деформації, а про деформації в пружною стадії, тобто без виникнення пластичних деформацій, і при однаковому навантаженні.
Перетворимо закон Гука, замінивши з рівняння (3.3):
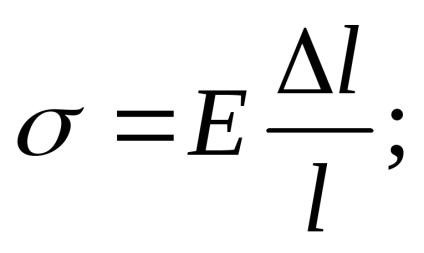
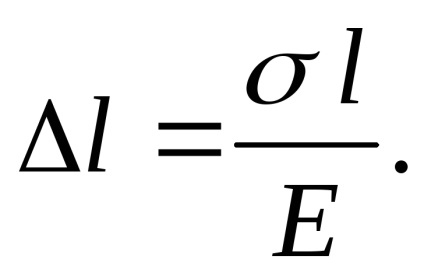
підставами значення

Ми отримали формулу для абсолютного подовження (укорочення) стрижня. при розтягуванні

При розтягуванні стрижень стає тоншою, при стисненні товщі. Зміна розмірів поперечного перерізу називається поперечної деформацією. Наприклад, у прямокутного перетину до навантаження були ширина b і висота перерізу h. а після навантаження b1 і h1. Відносна поперечна деформація для ширини перерізу:
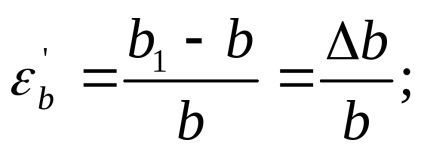
для висоти перерізу:
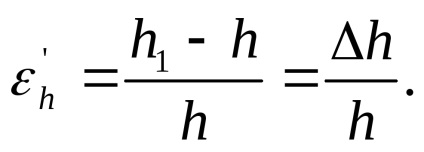
У ізотропних матеріалів властивості однакові в усіх напрямках. Тому:
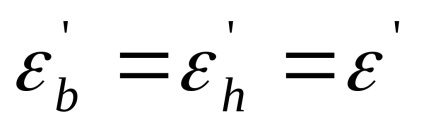
При розтягуванні поперечна деформація негативна, при стисненні позитивна.
Ставлення поперечної деформації до поздовжньої називається коефіцієнтом поперечної деформації або коефіцієнтом Пуассона:
Експериментально встановлено, що в пружною стадії роботи будь-якого матеріалу значення
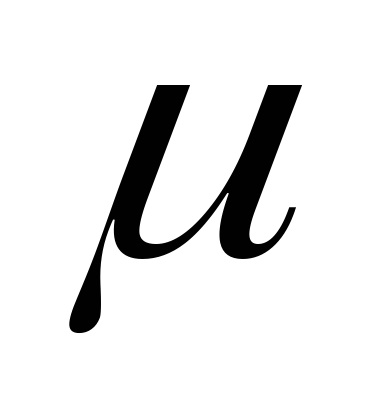
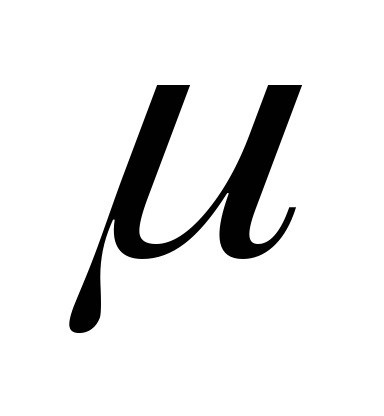
Із залежності (5) можна отримати наступну формулу:
При розтягуванні (стисканні) поперечним перерізом бруса переміщуються в поздовжньому напрямку. Переміщення є наслідком деформації, але ці два поняття потрібно чітко розмежовувати. Для стрижня (див. Рис. 3) визначимо величину деформації і побудуємо епюру переміщень.
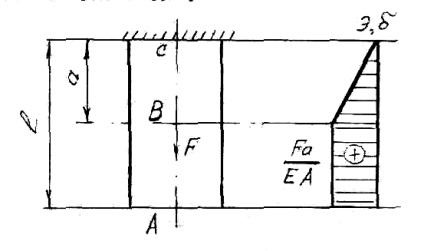
Як видно з малюнка відрізок стрижня АВ не розтягується, але переміщення отримає, так як подовжиться відрізок СВ. Його подовження одно:
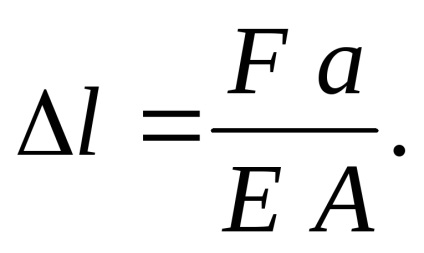
Переміщення поперечних перерізів позначимо через



3. Статично невизначені завдання
Статично визначити неможливо прийнято вважати системи, зусилля в яких не можна визначити за допомогою тільки рівнянь статики. Всі статично невизначені системи мають "зайві" зв'язку у вигляді додаткових кріплень, стрижнів і інших елементів. "Зайвими" такі зв'язки називають тому, що вони не є необхідними з точки зору забезпечення рівноваги системи або її геометричної незмінюваності, і їх пристрій переслідує конструктивні або експлуатаційні мети.
Різниця між кількістю невідомих і кількістю незалежних рівнянь рівноваги, які можна скласти для даної системи, характеризує число зайвих невідомих або ступінь статичної невизначеності.
Статично невизначені системи вирішують шляхом складання рівнянь переміщення певних точок, кількість яких має дорівнювати ступеня невизначеності системи.
Нехай на стрижень, жорстко закріплений обома кінцями, діє сила F (див. Рис. 4). Визначимо реакції опор.
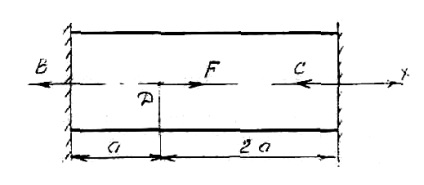
Реакції опор направимо вліво, так як сила F діє вправо. Оскільки вага сили діють по одній лінії можна скласти лише одне рівняння статичної рівноваги:
Отже, дві невідомі реакції опор В і С і одне рівняння статичної рівноваги. Система один раз статично невизначена. Отже, для її вирішення потрібно скласти одне додаткове рівняння, засноване на переміщеннях точки С. Подумки відкинемо праву опору. Від сили F ліва частина стрижня ВД буде розтягуватися і перетин С зміститься вправо на величину цієї деформації:
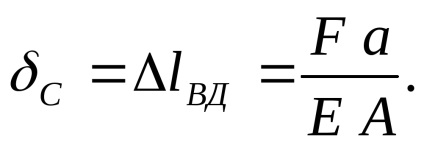
Від реакції опори С стрижень буде стискатися і перетин переміститься вліво на величину деформації всього стержня:
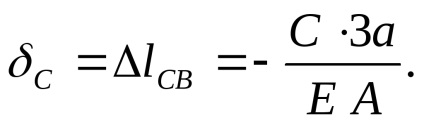
Опора не дозволяє перетину З переміщатися ні вліво, ні вправо, тому сума переміщень від сил F і С повинна дорівнювати нулю:
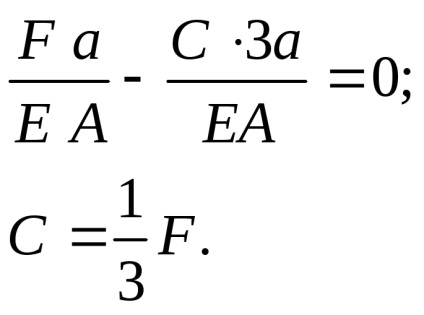
Підставивши значення С в рівняння статичної рівноваги, визначимо другу реакцію опори:
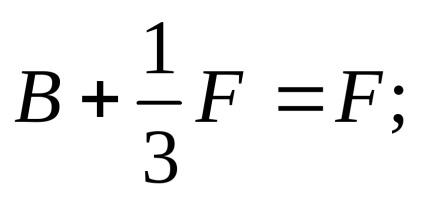
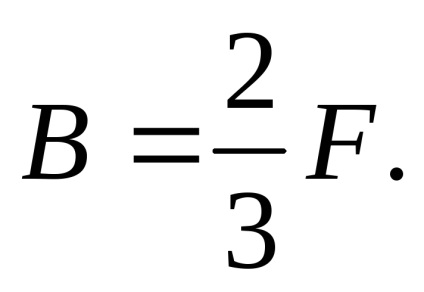
4. Температурні напруги
У статично невизначених системах при зміні температури можуть виникати напруги. Нехай стрижень, жорстко закріплений з двох кінців нагрівається на температуру

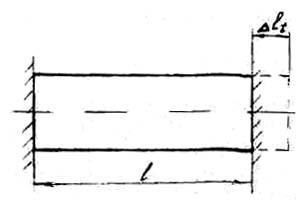
При нагріванні тіла розширюються, і стрижень буде прагнути подовжиться на величину:
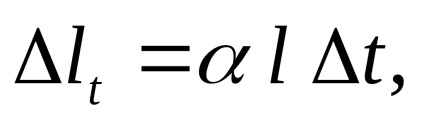
де

l первісна довжина.
Опори не дають можливості стрижня подовжиться, тому стрижень стискається на величину:
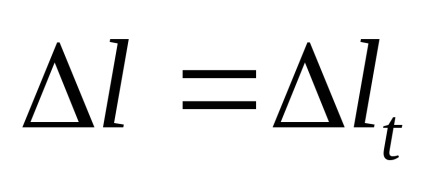
Відповідно до формули (4):
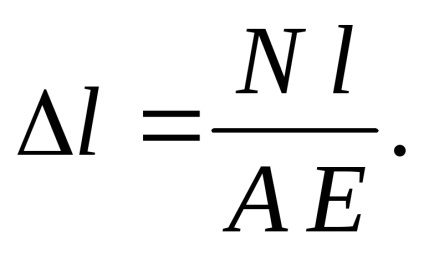
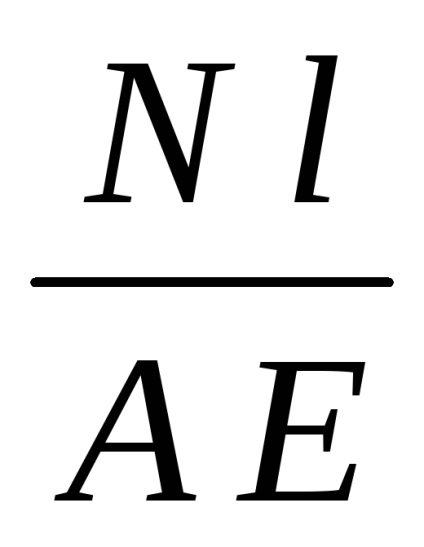
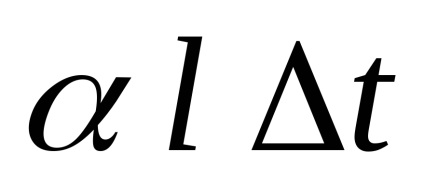
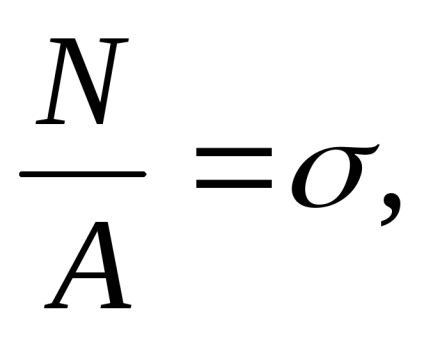
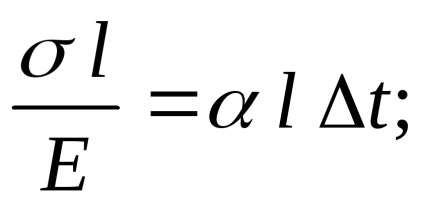
Як видно з формули (7) температурні напруга не залежать від довжини стержня, а залежать лише від коефіцієнта лінійного розширення, модуля поздовжньої пружності і зміни температури.
Температурні напруги можуть досягати великих значень. Для їх зменшення в конструкціях передбачаються спеціальні температурні зазори (наприклад, зазори в стиках рейок) або компенсаційні пристрої (наприклад, коліна в трубопроводах).
5. Монтажні напруги
Елементи конструкції можуть мати відхилення в розмірах при виготовленні (наприклад, через зварювання). При складанні розміри не співпадають (наприклад, отвори під болти), і прикладаються зусилля, щоб зібрати вузли. В результаті в елементах конструкції виникають внутрішні зусилля без додатка зовнішнього навантаження.
Нехай між двох жорстких заделок вставлений стрижень, довжина якого на величину а більше відстані між опорами (див. Рис. 6). Стрижень буде відчувати стиснення. Визначимо напруги, використовуючи формулу (4):
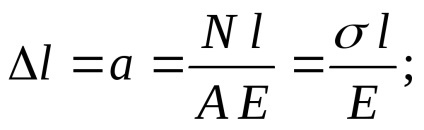

Як видно з формули (8) монтажні напруги прямо пропорційні похибки в розмірах а. Тому бажано мати а = 0. особливо для стрижнів невеликої довжини, так як

Однак в статично невизначених системах до монтажних напруженням спеціально вдаються, щоб підвищити несучу здатність конструкції.