Сортування - один з найбільш складних і важливих для вивчення алгоритмів.
По-перше, сортування - це спільне завдання багатьох комп'ютерних програм. Практично будь-який список цінніше, коли він впорядкований по якогось певного принципу.
По-друге, багато алгоритми сортування є цікавими прикладами програмування, що демонструють важливі методи: приватна упорядкування, рекурсія, об'єднання списків, збереження двійкових дерев в масивах.
У кожного алгоритму сортування є свої переваги і недоліки. Продуктивність різних алгоритмів залежить від типу даних, початкового розташування, розміру і значень. Важливо вибрати той алгоритм, який найкраще підходить для вирішення конкретного завдання.
Сортування - одна з небагатьох завдань з точними теоретичними межами продуктивності. Будь алгоритм сортування, який використовує порівняння, займає по крайней мере, O (N * logN) часу.
Сортування вибором
Сортування вибором - це простий алгоритм O (N 2). Його завдання - шукати найменший елемент, який потім міняється місцями з елементом з початку списку. Потім знаходиться з решти елементів і міняється місцями з другим елементом. Процес триває до тих пір, поки всі елементи не займуть своє кінцеве становище.
Визначається найменший елемент a7 = 1
Міняється місцями з першим 1 4 5 3 10 8 2
В останньому знову шукається мінімальний і змінюється з другим 1 2 5 3 10 8 4
1 2 3 5 10 8 4 1 2 3 4 10 8 5 1 2 3 4 5 8 10 1 2 3 4 5 8 10
Для реалізації цього алгоритму необхідні вкладені цикли For. Зовнішній цикл (поI) призначений для послідовного фіксування елементів масиву, внутрішній (поJ) - здійснює пошук мінімуму (максимуму) і його позиції. Після виходу з внутрішнього циклу слід перестановка елементів. Останній елемент у зовнішньому циклі не розглядається: він сам стане на своє місце.
При пошуку i-го найменшого елемента алгоритм повинен перевірити кожен ізN-Iоставшіхся. Час виконання алгоритму равноN + (N-1) + (N-2) + ... + 1 іліO (N 2).
Сортування вибором працює досить добре зі списками, де елементи розташовані випадково або в прямому порядку, але для назад відсортованих списків продуктивність цього алгоритму трохи гірше. Для пошуку мінімального елемента списку сортування вибором виконує наступну послідовність операторів:
If a (j) Якщо список впорядкований в зворотному порядку, умова a (j) Це не найшвидший алгоритм, але він дуже простий, а також швидко сортує невеликі списки. Сортування вставкою - ще один алгоритм складності O (N 2). Заснований на впровадженні в відсортовану частину масиву елемента, наступного за цією частиною, якщо він задовольняє умові сортування. Алгоритм переглядає вихідний список в порядку зростання і шукає місце, де необхідно вставити новий елемент. Потім він поміщає новий елемент в знайдену позицію. На першому проході другий елемент порівнюється з першим, на другому - третій елемент порівнюється з першим і другим і т.д. Якщо перевіряється i + 1-ий елемент задовольняє умові сортування средіiелементов, то він вставляється наj-е місце без порушення порядку, тобто елементи з індексами> = jі <=i-1 увеличивают свой индекс на 1. For i = 2 To n 'порівняння завжди починається b = a (i): j = 1' з першого Do While b> a (j) 'визначається номер j = j + 1' для вставки Loop For k = i To j + 1 Step -1 'звільняється a (k) = a (k - 1)' місце для вставки Next ka (j) = b 'здійснюється вставка For l = 1 To n Picture2.Print a (l); ""; Next Picture2.Print Next I End Sub Всього проходів n-1. Подібний алгоритм багато часу витрачає на пошук правильної позиції для нового елемента. Працює повільніше, ніж сортування вибором. Бульбашкова сортування - це алгоритм, призначений для сортування списків, які вже знаходяться в майже упорядкованому стані. Якщо ця умова виконана, то алгоритм виконується дуже швидко, за час порядку O (N). Якщо елементи спочатку розташовані в довільному порядку, алгоритм виконується заO (N 2) кроків. При бульбашкового сортування список проглядається до тих пір, поки не знайдуться два суміжних елемента, які слідують не по порядку. Вони міняються місцями, і список продовжує досліджуватися далі. Після першого проходу на першому місці (за зростанням) виявиться найменший елемент. Наступний прохід буде здійснюватися до цього елемента, тобто сортується решта масиву. Алгоритм повторює цей процес, поки не впорядкує всі елементи.Сортування вставкою
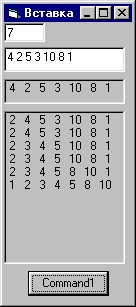
бульбашкова сортування
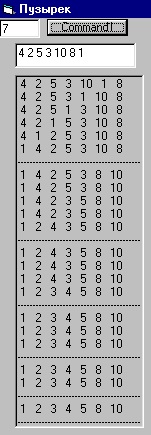

Пірамідальна сортування (бінарні дерева)
Піраміда - повне бінарне дерево, в якому кожен вузол більше, ніж його два дочірніх. Обидва дочірніх вузла, повинні бути менше, ніж батьківський, але будь-який з них може бути більше іншого. Кореневої вузол завжди найбільший в піраміді.
Будь-масив можна представити у вигляді піраміди, помістивши перший елемент масиву в корінь піраміди.
Наприклад, 2 4 5 3 10 8 1
Піддерево, що починається в будь-якому вузлі піраміди, теж є пірамідою.
Використовуючи цей факт, можна побудувати піраміду від низу до верху. З кожного з піддерев з трьома вузлами потрібно сформувати піраміду. Для цього потрібно порівняти верхній вузол з двома його дочірніми. Якщо будь-який з дочірніх вузлів більше, потрібно поміняти його з верхнім вузлом. Якщо обидва дочірніх вузла більше, потрібно поміняти з батьківський з великим з дочірніх. Цей крок повторюється до тих пір, поки всі піддерева не стануть пірамідами:
Потім, створюються більш великі піраміди: маленькі піраміди з вершинами 10 і 8 об'єднуються з елементом 2.
У підсумку на самій вершині піраміди виявляється максимальний елемент послідовності. Викидаємо його з піраміди, а на його місце ставимо крайній праворуч елемент на нижньому рівні. І знову будуємо піраміду. На вершині отримуємо наступний найбільший елемент і т. Д.