Привіт, дорогі студенти вузу аргемони! Рада бачити вас на черговий лекції магії функцій і інтегралів.
Сьогодні у нас на порядку денному - вивчення, перш за все, магії параболи. Ось з неї і почнемо.
Загальний вигляд параболи (квадратична функція)
Коефіцієнти b і c можуть дорівнювати нулю (одночасно чи ні), а ось коефіцієнт "a" нулю бути рівним не може, інакше це вже буде не квадратична функція.
Найпростіша функція параболи має вигляд
Бачимо, що особливостей ця функція не має. Значить, областю визначення є вся числова пряма (-∞; + ∞), а безліччю значень - тільки неотрицательная частина прямої [0; + ∞).
А зараз ми, користуючись знаннями отриманими на попередніх уроках, спробуємо за допомогою магії коефіцієнтів міняти магію функції.
Додавання коефіцієнта "а", відмінного від 1, призводить до зміни розмаху гілок параболи. Якщо | a |> 1, то парабола стає вже, а якщо | a |<1, то ветви расходятся в стороны и парабола становится шире.
Розглянемо тепер ось таку функцію
Додавання константи "з" в якості доданка до вираження з квадратом призводить до переміщення параболи вгору або вниз на "з" позицій. Відповідно, змінюється безліч значень функції.
Ну, а тепер можна здогадатися, що додавання доданка bx, очевидно, призведе до переміщення параболи по горизонталі.
Розберемо цей момент більш докладно. Спробуємо виділити в вираженні (1) повний квадрат. Насправді, коли в рівнянні присутні числові коефіцієнти, все набагато зрозуміліше, тому давайте перейдемо від буквених коефіцієнтів до числовим:
a = 2; b = 4; c = 5
y = 2x 2 + 4x + 5 = 2 (x + 1) 2 +3
І ось тепер акуратно почнемо розбирати магію цієї квадратичної функції. Почнемо зсередини.
Бачимо, що в квадраті НЕ х, а (х + 1). З попередніх уроків ми пам'ятаємо, що коефіцієнт-доданок поруч з х викликає магію переміщення функції по горизонталі вправо або вліво. У нашому випадку на 1 одиницю вліво.
Далі звертаємо увагу на коефіцієнт 2 близько квадрата. Він викличе магію стиснення параболи. Вона стане вже. Якби цей коефіцієнт був ще й негативним, то парабола б повернулася на 180 градусів, і гілки б стали б дивитися вниз.
Далі в дію вступає коефіцієнт 3 і застосовує свою магію, викликаючи пересування параболи на 3 одиниці вгору.
Завдання 1. Кожен бере свою параболу (1).
Коефіцієнти визначаються наступним чином:
а = першого числа в номері вашого ЛД
b = другого числа в номері вашого ЛД
c = третього числа в номері вашого ЛД або a-b, якщо номер вашого ЛД двозначний.
Треба досліджувати цю параболу так само, як робили ми на уроці, зазначивши і проміжки спадання і зростання.
Урок ще не закінчений. Підемо далі. Положення параболи в координатних осях залежить від коефіцієнтів a, b, c.
Від знака коефіцієнта а залежить, як спрямовані гілки параболи:
якщо а> 0, то гілки параболи спрямовані вгору;
якщо а<0, то ветви параболы направлены вниз.
Думаю, ви пам'ятаєте, як шукаються корені квадратного рівняння, відповідного квадратичної функції,
Так-так, через обчислення дискримінанту. Корній може бути 2, може бути один (насправді коренів 2, але вони однакові), або не бути коренів. Але немає дійсних коренів, а ось уявні корені є, але про такі корінні ми говорити поки не будемо, хоча вони відкривають ще більш цікаву магію, але про неї пізніше. набагато пізніше. Якщо вас зацікавить це, то ми потім повернемося до уявних коренів і магії функції комплексної змінної. А її магія ще більш дивна, і вона може творити такі дива, які багатьом і не снилися. Але поки будемо говорити тільки про дійсних коренях квадратного рівняння.
Отже, якщо коріння 2, то це означає, що парабола перетинає вісь ОХ в двох точках.
Якщо корінь один (вірніше, два однакових), то це означає, що парабола стосується осі ОХ в одній точці.
Якщо ж дискримінант квадратного рівняння, відповідного квадратичної функції, негативний, то вся парабола знаходиться або вище осі ОХ, або нижче неї.
Ще раз зверну вашу увагу на те, що областю визначення параболи є вся числова вісь, а ось безліч значень залежить від положення параболи.
Завдання 2. У наведених мною вище графіках, вважаючи масштаб 1: 1, вкажіть безліч значень всіх функцій 1-6.
І тепер швиденько познайомимося з загальним видом статечної функції
y = x n. n-натуральне число (4)
Ясно, що коли n-парне число, то вид функції схожий на (1).
Якщо n-непарне число, то графік функції перестає бути парним, він стає непарних і виконується умова f (-x) = - f (x). Такий вид функції ще називається кубічної параболою.
Завдання 3. Знайдіть область визначення і множину значень для функції (4) для різних n (парних і непарних).
І, нарешті, останнє. Розглянемо функцію, зворотну функції (4). Яка операція зворотна зведенню в ступінь? Звичайно ж, добування кореня.
Тут теж необхідно розглянути два випадки.
1. n-парне. Область визначення - невід'ємна піввісь [0; + ∞), тому що з негативного числа можна витягти корінь парного степеня.
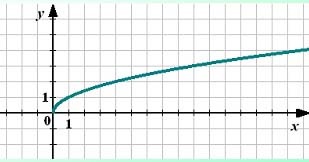
2. n - непарне число. Графік має такий вигляд
Завдання 4. Вкажіть для функції (5) області визначення і множина значень. Порівняйте графіки функцій (4) і (5).
І в кінці покажу вам, як будуються графіки обернених функцій. Графіки зворотних функцій симетричні відносно бісектриси 1 і 3 координатних кутів. Тому досить провести цю лінію і відобразити симетрично відносно неї графік статечної функції.
На малюнку я зобразила обидва випадки статечних функцій і зворотних до неї. Як ми бачимо, у випадку з n-непарним все нормально: обидві гілки відбилися симетрично бісектриси, і вийшла функція. А ось у випадку з n-парним одна з гілочок намальована пунктиром, бо вона не входить в графік функції, тому що вийшла симетричним відображенням крива функцією не буде.
Завдання 5. Покажіть, що якщо включити і пунктирну гілку в графік, то це вже буде графік не функції.
Надсилайте роботи через ОСОБИСТИЙ КАБІНЕТ
Свої запитання сміливо можете передати з Персефоной
Краща пропозиція в салоні jaguar xj від офіційного дилера.