
Головна | Про нас | Зворотній зв'язок
Як вказувалося в попередньому розділі, для розрахунку часу поширенням странения світлових імпульсів в дисперсійному середовищі використовується груповий показник заломлення Nгр. і групове час поширення tгр яке для дисперсійного середовища довжиною L визначається так:
Джерело світла, як правило, випромінює світло не на одній довжині хвилі # 955 ;, а з спектральної шириною # 8710; # 955 ;, тому окремі порції світла в межах Nгр. поширюються з різними швидкостями і мають різні затримки ча-мени.
Якщо середовище поширення дисперсійна і ширина спектра джерела випромінювання становить # 8710; # 955 ;, то в процесі поширення світловий імпульс розширюється і надходить на вихід середовища протягом часу
Вираз називається питомою матеріальної дисперсією, пс / км # 8729; нм.
Вираз для розрахунку питомої матеріальної дисперсії можна напів-чить з (2.28):
На рис. 2.14 показана залежність питомої матеріальної дисперсії. Для чистого кварцу на довжині хвилі # 955; = 0,85 мкм величина М (# 955;) - 85 пс / км # 8729; нм, при цьому з ростом довжини хвилі її значення зменшується і проходить через нуль при # 955; = 1,276 мкм.
Таким чином, після проходження світловим імпульсом відстані L в дисперсійному середовищі він розширюється, причому його тривалість т на рівні половинної потужності визначається виразом
Як видно, розширення імпульсів залежить від довжини середовища і ширини спік-тра джерела випромінювання. І так як ширина спектра випромінювання у світлодіодів значно більше, ніж у лазерів, то і розширення імпульсів буде значно більше.
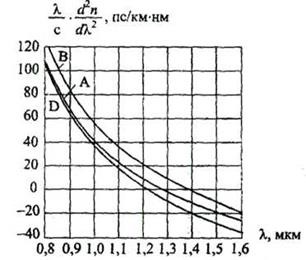
Мал. 2.14. Залежність питомої матеріальної дисперсії від довжини хвилі: А - чистий кварц;
Зазвичай ширину спектра # 8710; # 955; джерела випромінювання визначають як діапа-зон довжин хвиль, в межах якого випромінюється їм потужність перевищує 50% максимального значення.
Однак досить часто використовується поняття відносної ширини у спектру випромінювання джерела
тоді після проходження світловим імпульсом відстані L в дисперсійному середовищі його тривалість на рівні половинної потужності
- є коефіцієнт дисперсії матеріалу.
На рис. 2.15 представлені залежності коефіцієнта дисперсії мате-ріалу Yм від довжини хвилі для чистого і легованого кварцу.
Як видно, крива Yм (# 955;) так само як і М (# 955;) змінює знак на довжині хвилі # 955; = # 955; 0 = 1,276 мкм. Це значення відповідає точці перегину кривої п (# 955;) (рис. 2.10). У літературі часто це значення довжини хвилі визначають як «довжину хвилі нульової дисперсії матеріалу». З практичної точки зору та-де визначення вводить в оману, так як реальний світловий імпульс з-тримає в собі спектр довжин хвиль, які поширюються з груповими ско-зростання, що лежать в деякому інтервалі, навіть якщо найкоротша і найдовша хвилі поширюються з однаковими швидкостями.
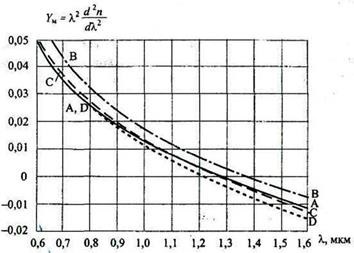
Мал. 2.15. Залежно дисперсійного параметра Yм від довжини хвилі: А - чистий кварц; В - 13,5% GeO2, 86,5% SiO2; С - 9,1% Р2 О5, 90,9% SiO2; D - 13,3,% В2 О3, 86,7% SiO2
Для кварцу на довжині хвилі # 955; = # 955; 0 = 1,276 мкм, Yм = 0, тому
Для чистого кварцу на довжині хвилі # 955; = # 955; 0 = 1,276 мкм значення = -0,048, отже, (2.38) набирає вигляду, нс / км:
Для світлодіодів значення # 947; = 0,04, тому дисперсія # 964; / L = 32 пс / км.
При використанні лазерних джерел випромінювання значення дисперсії буде на 2 порядки менше.
Дисперсія матеріалу залежить від його складу. Так, за допомогою легірова-ня чистого кварцу можна змінити її значення в певних межах і тим самим вплинути на становище «нульової точки». величину # 955; 0 можна змінити, вводячи різні добавки в кварцове скло. Як видно з рис. 2.15, введення бору може зробити її менш 1,22 мкм, а легування германієм по-зволяет підняти її до 1,37 мкм.
Розширення імпульсу на довжині хвилі # 955; 0 у випадку з джерелом з Гаусса-вим спектром визначається співвідношенням
де значення визначає нахил кривої питомої дисперсії матеріалу,
Значення коефіцієнтів Аi і bi для стекол різних складів приведені в табл. 2.2. для
На закінчення слід зазначити, що довжина хвилі нульової дисперсії # 955; 0 = 1,276 мкм відповідає об'ємної середовищі. Для оптичного волокна ця довжина хвилі зсувається до значення близько 1,312 мкм, чим і пояснюється ис-користування джерел випромінювання 1,310 мкм для одномодового волокна.
З точки зору геометричної оптики світловий імпульс являє собою сукупність великої кількості променів світла, що поширюються в серд-цевіне ОВ, а з точки зору хвильової теорії # 9472; сукупність безлічі на-правляться мод (типів хвиль).
Різниця шляхів поширення направляються мод на фіксованій частоті (довжині хвилі) випромінювання оптичного джерела призводить до того, що час проходження цих мод по ОВ-різному. В результаті утворюється ними імпульс на виході ОВ уширяется. Величина розширення імпульсу дорівнює різниці часу поширення найповільнішої і найшвидшою мод. Вказано-ве явище носить назву межмодовой дисперсії.
Формулу розрахунку межмодовой дисперсії можна отримати, розглядаючи геометричну модель поширення направляються мод в ОВ. Будь-яка на-правляться мода в ступінчастому ОВ може бути представлена світловим променем, який при русі вздовж волокна багаторазово відчуває повне внутрішнє віддзеркалення від поверхні розділу «серцевина-оболонка». Исключени третьому є основна мода НЕ11, яка описується світловим променем, рухаємося-щимся без відображення уздовж осі волокна.
При довжині ОВ (рис 2.16), яка дорівнює L, довжина зиґзаґоподібного шляху, прой-денного променем світла, що поширюється під кутом # 952; z до осі волокна, склад-ляет L / cos # 952; z.
Мал. 2.16. Шляхи поширення світлових променів в двошаровому ОВ
Швидкість поширення електромагнітних хвиль з довжиною хвилі # 955; оди-наково в розглянутому волокні і дорівнює U1 = с / n1, де с - швидкість світла, км / с. Отже, час поширення світлового променя в серцевині ОВ
Як видно (2.41), час поширення променя змінюється обернено про-порційно cos # 952; z. Значить, мінімальний час поширення tmin відпо-ствует # 952; z = 0, т. Е. Променів, що поширюється паралельно осі, а максималь-ное час поширення tmax відповідає # 952; z = # 952; кр. де # 952; кр - критичний кут падіння світлового променя на межу розділу серцевина-оболонка.
Таким чином, час поширення по найдовшому і Сама короткому шляху згідно (2.41):
Нехай на вхід ОВ подається дуже короткий імпульс. Початок вихідного імпульсу збігається з часом приходу променя, що пройшов найкоротший шлях, а кінець - з часом приходу променя, що пройшов найдовший шлях.
Отже, розширення імпульсу складе
Зазвичай в ОВ n1 ≈ n2. тому (2.43) набирає вигляду
де - відносне значення показників заломлення серцевина-оболонка.
З формули (2.44) видно, що розширення імпульсів, обумовлене межмодовой дисперсією, тим менше, чим менше різниця показників Ломлячи-ня серцевини і оболонки. Це одна з причин, чому в реальних ступенча-тих ОВ цю різницю прагнуть зробити якомога менше.
З (2.44) випливає й інший висновок: розширення імпульсів пропорційно протяжності ОВ. Однак це справедливо лише для ідеального ОВ, в кото-ром відсутня взаємодія між спрямованими модами. На практиці ж через наявність неоднорідностей (головним чином, микроизгибов) окремих-ні моди при проходженні по ОВ впливають один на одного і обмінюються енергією.
Моди нижчого порядку з малим кутом по відношенню до осі ОВ за рахунок обміну енергією перетворюються в моди вищого порядку з більш крутим кутом по відношенню до осі ОВ і навпаки. Внаслідок цього відмінність швидкостей мод вирівнюється. У геометричній трактуванні це означає, що через неоднорідний-ностей одні і ті ж промені змінюють кути, під якими вони поширюються по серцевині ОВ. При цьому зміна кутів і затримки компонент сигналу носять випадковий характер, а розкид часу поширення мод стає
Важливо відзначити, що дане явище проявляється, починаючи з визначений-ної довжини ОВ, яка носить назву «довжини усталеною зв'язку між модами» - Ly, і залежить від багатьох випадкових факторів, але точно розрахована бути не може. За даними вимірів для східчастих ОВ Ly = 5 # 9472; 7 км.
Таким чином, межмодовая дисперсія в ОВ із ступінчастим профілем показника заломлення
Межмодовую дисперсію в східчастих ОВ можна повністю виключним видом-чить, якщо відповідним чином підібрати структурні параметри ОВ. Так, якщо зробити розміри серцевини і # 8710; настільки малими, то по волокну буде поширюватися на несучої довжині хвилі тільки одна мода, т. е. модів дисперсія буде відсутній. Такі волокна називаються одномодовими. Вони мають найбільшу пропускну здатність. З їх допомогою можуть бути організовані великі пучки каналів на магістралях зв'язку.
Дисперсія імпульсів може бути також істотно зменшена за рахунок відповідного вибору профілю заломлення по перетину серцевини ОВ. Так, дисперсія зменшується при переході до градієнтним ОВ. Межмодовая дисперсія градієнтних ОВ, як правило, нижче на порядок і більш ніж у сту-пенчатих волокон.
У таких градієнтних ОВ на противагу ОВ із ступінчастим про-Філем поширення, промені світла поширюються вже не зигзагоподібно, а по хвиле- або гвинтоподібним спіральних траєкторіях (рис 2.17).
Мал. 2.17. Шляхи поширення світлових променів в ОВ з параболічної залежністю показника заломлення
Промені, що поширюються навколо осі ОВ, проходять довший шлях, ніж промінь світла вздовж осі ОВ. Однак завдяки меншій показником заломлення на віддалі від осі ОВ, ці промені поширюються в середовищі з меншим п відповідно швидше, а промені, що поширюються уздовж осі, проходять менший геометричний шлях, але поширюються в середовищі з біль-шим п, т. Е. З меншою швидкістю. В результаті час поширення променів вирівнюється, і збільшення тривалості імпульсу стає менше.
В градієнтних багатомодових волокнах час поширення оптич-ських променів визначається законом зміни показника заломлення.
Так, межмодовая дисперсія в градієнтних ОВ з параболічним профі-лем показника заломлення qопm = 2, який широко використовується па практи-ке, розраховується за формулою
При оптимальному профілі показника заломлення qопm ≈ 2 (1 - # 916;) дисперсія імпульсів мінімальна:
За даними вимірів значення для градієнтного ОB Ly = 10-15 км.
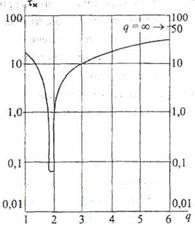
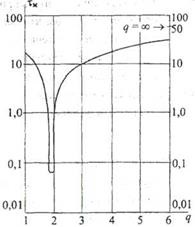
межмодовая дисперсія # 964; мм в гра-діентних ОВ залежить від ступеня q, по-цьому для мінімізації дисперсії НЕ-обходимо ретельно підбирати зна-ня q (рис. 2.18).
Зміна профілю, прибл-лишнього до параболічного, суще-ного зменшує межмодовую дис-персію в такому градиентном ОВ. Од-нако виготовити оптимальний параболічний профіль показника заломлення складно Поряд з відхиленням значення q від необхідного можлива поява осьового провалу показника заломлення, пульсацій і інших позову-жений профілю, які на порядок і більше збільшують межмодовую дисперсію. Типова величина розширення імпульсів в отриманих ОВ з опти-ною параболічних профілем становить 0,2-4,0 НЕ / км.
Рис 2.18. залежність # 964; м від q
для градієнтних ОВ