1) Дія перша. Винесення мінуса з матриці (внесення мінуса в матрицю).
Винесемо мінус за межі матриці, змінивши у КОЖНОГО елемента матриці знак:
Внесемо мінус в матрицю, змінивши у КОЖНОГО елемента матриці знак.
2) Дія друга. Множення матриці на число.
Єдине, що бажано зробити в цьому прикладі - це внести мінус в матрицю: А ось якби ВСІ елементи матриці ділилися на 7 без залишку. то тоді можна (і потрібно!) було б поділити.
3) Дія третя. Транспонування матриці.
Потім переписуємо другий рядок у другій стовпець:
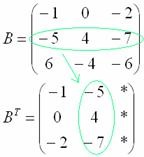
4) Дія четверта. Сума (різниця) матриць.
НЕ ВСЕ МАТРИЦІ можна складати. Для виконання додавання (віднімання) матриць, необхідно, щоб вони були однаковими за розміром.
Дія п'ята. множення матриць
Щоб матрицю можна було помножити на матрицю потрібно, щоб число стовпців матриці дорівнювало числу рядків матриці.
- спробуйте відразу вловити закономірність.
Помножити матрицю на матрицю
Зверніть увагу, що ! Це майже завжди так!
Таким чином, при множенні переставляти матриці можна!
Визначники, властивості, алгебраїчні доповнення, обчислення
Позначення. Якщо дана матриця. то її визначник позначають. Також дуже часто визначник позначають латинською літерою або грецької.
Отже, визначник «три на три» зводиться до вирішення трьох маленьких визначників, або як їх ще називають, мінор. Термін рекомендую запам'ятати, тим більше, він запам'ятовується: мінор - маленький.
Коль скоро обраний спосіб розкладання визначника по першому рядку. очевидно, що все обертається навколо неї:
1) З матриці знаків виписуємо відповідний знак:
2) Потім записуємо сам елемент:
3) подумки викреслюємо рядок і стовпець, в якому стоїть перший елемент:
Чотири числа і утворюють визначник «два на два», який називаетсяМІНОРОМ даного елемента (одиниці).
Переходимо до другого елементу рядка.
4) З матриці знаків виписуємо відповідний знак:
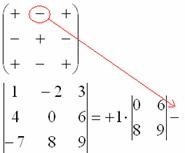
5) Потім записуємо другий елемент:
6) подумки викреслюємо рядок і стовпець, в якому стоїть другий елемент:
Чотири числа записуємо в маленький визначник.
Ну і третій елемент першого рядка. Ніякої оригінальності:
7) З матриці знаків виписуємо відповідний знак:
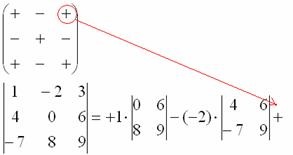
8) Записуємо третій елемент:
9) подумки викреслюємо рядок і стовпець, в якому стоїть третій елемент:
1. Визначник вигідніше розкривати по ТОЙ рядку (стовпцю), де:
З чого випливає важливий факт: рядки і стовпці визначника рівноправні.
2. Якщо два рядки (або два стовпці) визначника поміняти місцями,
то визначник змінить знак
Тобто, будь-яка парна перестановка рядків (стовпців) тягне зміна знака визначника на протилежний.
3. З рядка (стовпчика) визначника можна винести загальний множник
Справедливо і зворотне правило - множник можна не тільки винести, але і внести. причому, в БУДЬ-ЯКУ рядок або в будь-стовпець визначника.
4. Якщо два рядки (стовпці) визначника пропорційні
(Як окремий випадок - однакові), то даний визначник дорівнює нулю
Визначник з нульовою рядком (стовпчиком) дорівнює нулю
Які властивості визначників корисно знати?
1) Величина визначника не змінюється при транспонировании. Властивість запам'ятовуємо.
2) Будь-яка парна перестановка рядків (стовпців) змінює знак визначника на протилежний. Властивість теж запам'ятовуємо і намагаємося не використовувати, щоб уникнути плутанини.
3) З рядка (стовпчика) визначника можна винести множник (і внести його назад). Використовуємо там, де це вигідно.
Якщо рядки (стовпці) визначника пропорційні, то він дорівнює нулю. Визначник з нульовою рядком (стовпчиком) дорівнює нулю.
Система лінійних рівнянь теорема Крамера
Запис систем лінійних рівнянь в матричній формі