Лабораторна робота N 2.
ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ МАЯНІКА Обербека
Мета роботи: Визначити момент інерції маятника Обербека, використовуючи закон збереження і перетворення енергії, і вивчити залежність моменту інерції від розташування мас на хрестовинах.
Прилади та приладдя
ПІДГОТОВКА ДО РОБОТИ
За лекцій і списку літератури вивчити наступні теоретичні питання:
ТЕОРІЯ МЕТОДУ ИЗМЕРЕНИЙ І ОПИС УСТАНОВКИ
Маятник Обербека (рис. 1) складається з чотирьох стрижнів і двох шківів різного радіусу, укріплених на одній горизонтальній осі обертання. За стержнів можуть переміщатися і закріплюватися в потрібному положенні чотири (по одному на кожному стрижні) вантажу однаковою маси m 0.
На один з шківів радіуса r 1 або R 2 намотується нитка, до кінця якої кріпиться платформа з вантажем. Нехай m 1 - маса платформи, а m 2 - маса вантажу, тобто загальна маса: m = m 1 + m 2.
Якщо вантаж m підняти на деяку висоту h 1 і відпустити, то вантаж прийде в рух, а сила натягу Тн розмотуваної зі шківа нитки створить обертовий момент М. При симетричному розташуванні вантажів на хрестовині це буде єдиний діючий на систему обертається момент.
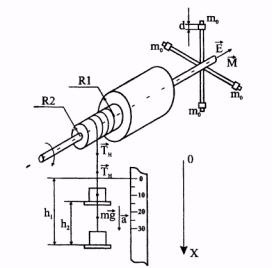
Нехай в початковий момент часу (t = 0) нерухома платформа з вантажем знаходиться на висоті h 1. Повна механічна енергія вантажу визначатиметься потенційною енергією:
При русі вантажу потенційна енергія переходить в кінетичну енергію платформи з вантажем і кінетичну енергію обертання маятника У момент часу t 1. коли платформа з вантажем підходить до нижнього положення, повна енергія системи «маятник Обербека і платформа з вантажем» дорівнює:
де - кінетична енергія поступального руху платформи з вантажем;
- кінетична енергія обертового маятника;
I - момент інерції маятника щодо осі обертання.
Слід зауважити, що в крайньому положенні (коли нитка повністю розмоталася) вантаж з платформою продовжує рухатися вниз, викликаючи деформацію пружною нитки. В цьому випадку кінетична енергія вантажу переходить в потенційну енергію деформації нитки. При русі вантажу вгору потенційна енергія знову переходить в кінетичну енергію вантажу.
При обертанні маятника і русі вантажу діє сила опору повітря, а в підшипниках на вісь обертання діє сила тертя. Нехай всі ці сили викликають загальний момент сили тертя МТР. Наявність сили тертя порушує закон збереження механічної енергії, так як частина її переходить у внутрішню енергію
Робота сили тертя при обертанні маятника:
де - кут повороту махового колеса при переміщенні платформи з вантажем на відстань h 1.
де R - радіус шківа
Згідно із законом збереження загальної енергії:
де - зміна повної енергії при переході платформи з верхньої точка в нижню:
Маятник продовжує обертатися в ту ж сторону і піднімає платформу з вантажем на висоту h 2. причому h 2 Спад повної енергії дорівнює роботі сил тертя при обертанні на всьому шляху руху вниз і вгору: Або, з урахуванням (5) і (1). вираз (6) запишемо: Так як рух маятника з вантажем равноускоренное з початковою швидкістю, що дорівнює нулю, то в нижчій точці швидкість вантажу: де а - прискорення платформи з вантажем, t 1 - час опускання вантажу. З рівнянь (9) і (10) можна виразити: Підставивши значення лінійної швидкості (11) в (12), отримаємо. Підставивши в рівняння (4) значення Мтр (8), v (11), (13), після перетворень отримаємо розрахункову формулу для обчислення моменту інерції маятника Обербека Результати вимірювань і обчислень занести в табл 1
де - кут повороту маятника при русі вантажу вниз на відстань h 1 і вгору - на h 2.
Оскільки нитка при русі вантажу змотується зі шківа без ковзання, лінійна швидкість точок, що лежать по поверхні шківа, дорівнює швидкості руху вантажу. Відомо, що кутова швидкість обертання пов'язана з лінійною швидкістю руху точки по колу рівністю:
ПОРЯДОК ВИКОНАННЯ РОБОТИ
Схожі статті