де xi -i -е реальне значення змінної вi -й момент часу, аx'i -i -е прогнозоване значення змінної вi -й момент часу, N - кількість прогнозів.
Згідно з результатами, отриманими на аркуші «Просте ск. середнє »робочої книги« ЛР6.Прімер 1.Станкі.xls »(див. Малюнок 56), ковзне середнє за три місяці має значення САО рівне 12,67 (осередок D16), тоді як для змінного середнього за 4 місяці значення САО дорівнює 15 , 59 (осередок F16). Тоді можна висунути гіпотезу, що використання більшої кількості статистичних даних швидше погіршує, ніж покращує точність прогнозу методом змінного середнього.
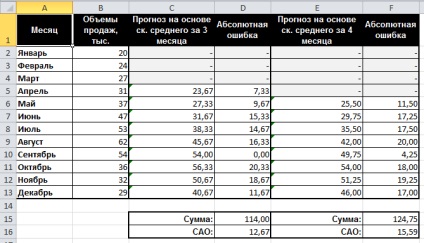
Малюнок 56. Приклад 1 - результати прогнозування методом простого ковзного середнього
На графіку (див. Малюнок 57), побудованому за результатами спостережень і прогнозів з інтервалом 3 місяці, можна помітити ряд особливостей, загальних для всіх застосувань методу змінного середнього.
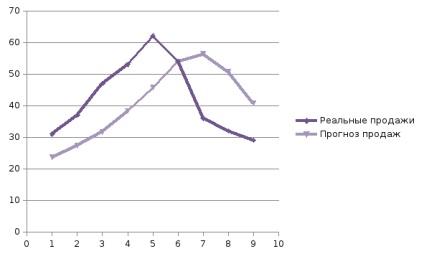
Малюнок 57. Приклад 1 - графік кривої прогнозу методом простого ковзного середнього і графік реального обсягу продажів
Значення прогнозу, отримане методом простого ковзного середнього, завжди менше фактичного значення, якщо вихідні дані монотонно зростають, і більше фактичного значення, якщо вихідні дані монотонно зменшуються. Тому, якщо дані монотонно зростають або зменшуються, то за допомогою простого змінного середнього можна отримати точних прогнозів. Цей метод найкраще підходить для даних з невеликими випадковими відхиленнями від деякого постійного або повільно мінливого значення.
Основний недолік методу простого змінного середнього виникає в результаті того, що при обчисленні прогнозованого значення найостанніше спостереження має таку ж вагу (т. Е. Значимість), як і попередні. Це відбувається тому, що вага всіх N останніх спостережень, що беруть участь в обчисленні змінного середнього, дорівнює 1 / N. Присвоєння рівного ваги суперечить інтуїтивному уявленню про те, що в багатьох випадках останні дані можуть більше сказати про те, що станеться в найближчому майбутньому, ніж попередні.
Виважена ковзне середнє. Внесок різних моментів часу можна врахувати, вводячи вага для кожного значення показника в ковзному інтервалі. В результаті виходить метод зваженого ковзного середнього, який математично можна записати так:
де - вага, з яким використовується показательпрі розрахунку.
Вага - це завжди позитивне число. У разі, коли всі ваги однакові, вироджується метод простого змінного середнього.
Тепер маркетолог може використовувати метод зваженого ковзного середнього за 3 місяці. Але перш потрібно зрозуміти, як вибрати ваги. Використовуючи засіб Пошук рішення, можна визначити оптимальну вагу вузлів. Щоб визначити вагу вузлів за допомогою засобу Пошук рішення, при якому значення середнього абсолютних відхилень було б мінімально, виконайте наступні дії:
Виберіть команду Сервіс -> Пошук рішення.
У діалоговому вікні Пошуку рішення встановіть осередок G16 цільової (див. Лист «Ваги»), мінімізуючи її.
Змінюваними осередками вкажіть діапазон В1: В3.
Встановіть обмеження В4 = 1,0; В1: ВЗ ≥ 0; В1: В3 ≤ 1; B1 ≤ В2 і В2 ≤ В3.
Запустіть пошук рішення (результат відображає).
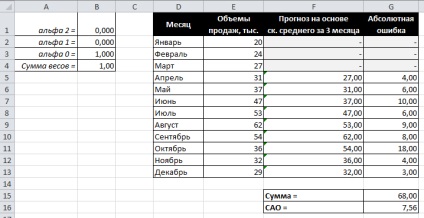
Малюнок 58. Приклад 1 - результат пошуку ваг значень показників при використанні методу зваженого ковзного середнього
Отримані результати показують, що оптимальний розподіл ваг таке, що вся вага зосереджений на самому останньому спостереженні, при цьому значення середнього абсолютних відхилень одно 7,56 (див. Також Малюнок 59). Цей результат підтверджує припущення про те, що більш пізні спостереження повинні мати більшу вагу.
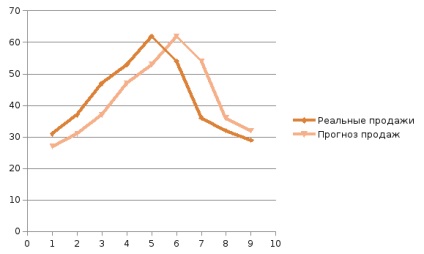
Малюнок 59. Приклад 1 - графік кривої прогнозу методом зваженого ковзного середнього і графік реального обсягу продажів