Число А називається границею функції y = f (х) при х, що прямує до нескінченності, якщо для будь-якого, навіть як завгодно малого позитивного числа e, знайдеться таке позитивне число S (залежне від e, тобто S = S (e) ), що для всіх х таких, що | х |> S, вірно нерівність: | f (x) - А | Відзначимо, що відмінність цього визначення від визначення меж послідовності полягає в тому, що для послідовності змінна n приймала тільки натуральні значення, а тут х приймає будь-які значення. Межа функції в нескінченності позначається або Сенс визначення полягає в тому, що для досить великих за модулем значеннях аргументу значення функції як завгодно мало відрізняються від числа А по абсолютній величині. Геометричний сенс визначення можна пояснити малюнком 2.3. Малюнок 2.3 - Геометричний сенс границі функції в нескінченності
f (x) ® А при x ® ¥.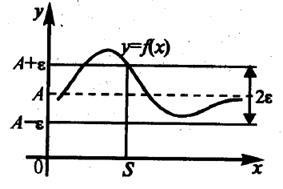
Отже, число А є межа функції у = f (x) при x ® ¥, якщо для будь-якого e> 0 знайдеться таке число S> 0, що для всіх х таких, що | х |> S, відповідні ординати графіка функції f ( x) будуть укладені в e-околиці точки А на осі ординат. При цьому відповідна частина графіка буде перебувати в смузі шириною 2 e.
Поняття границі функції в нескінченності можна сформулювати і при прагненні х до нескінченності певного знака. Відмінність полягатиме в тому, що аргумент функції необмежено зростає не по абсолютній величині, а x ® + ¥ (тоді у визначенні замість | х |> S буде стояти нерівність х> S) або x ® - ¥ (тоді у визначенні замість | х |> S буде стояти нерівність х <-S).
Межа функції в точці
Число А називається границею функції y = f (x) при х, що прямує до х0 (або вточке х0), якщо для будь-якого, навіть як завгодно малого позитивного числа e, знайдеться таке позитивне число d (залежне від e, тобто d = d (e)), що для всіх х ¹ х0 таких, що | х - х0 | Межа функції в точці х0 позначається або Сенс визначення полягає в тому, що для всіх значень аргументу, досить близьких до х0. значення функції як завгодно мало відрізняються від числа А по абсолютній величині. Геометричний сенс визначення можна пояснити малюнком 2.4.
f (x) ® А при x ® х0.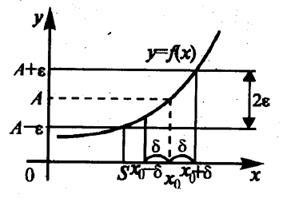
Малюнок 2.4 - Геометричний сенс границі функції в точці
Отже, число А є межа функції у = f (x) при x ® х0. якщо для будь-якого e> 0 знайдеться така d-околиця точки х0. що для всіх х ¹ х0 з цієї околиці відповідні ординати графіка функції f (х) будуть укладені в e-околиці точки А на осі ординат. При цьому відповідна частина графіка буде перебувати в смузі шириною 2 e.
Підкреслимо, що визначення меж не вимагає існування функції в самій точці х0. Розглядаючи межа, припускають, що х прагне до х0. але не досягає цього значення. Тому наявність або відсутність межі визначається поведінкою функції в околі точки х0. а не тим, визначена чи ні функція в самій цій точці.
Поняття границі функції в точці можна сформулювати і в сенсі одностороннього межі. Відмінність полягатиме в тому, що аргумент функції приймає лише значення x Якщо. то. і навпаки (тобто якщо в деякій точці функція має межі ліворуч і праворуч, і вони рівні, то двосторонній межа теж існує і дорівнює тому самому числу, і навпаки, - якщо існує двосторонній межа, то існують і односторонні, рівні йому ж ). Умова, що визначає поведінку аргументу, яке ми записували під позначенням межі, будемо називати базою межі і позначати В в запису.Схожі статті