Межі дрібно-раціональних функцій з квадратичними виразами

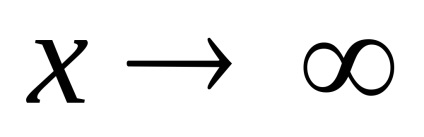
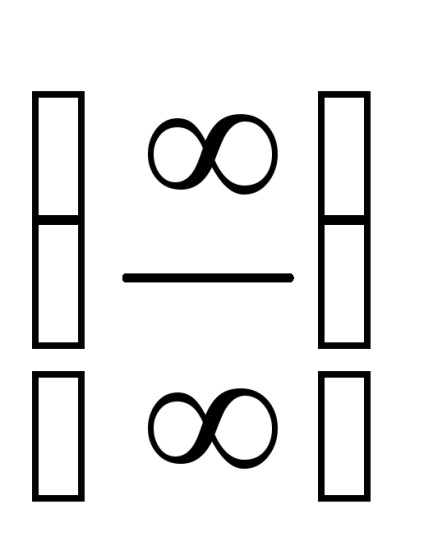
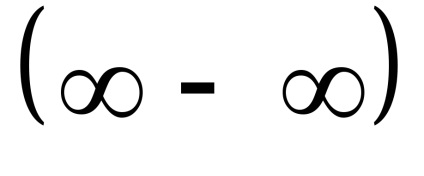
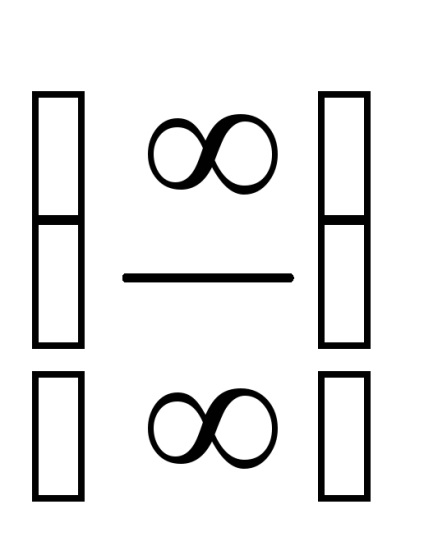
У разі невизначеності

слід розкласти квадратичне вираз на множники. Для цього можна

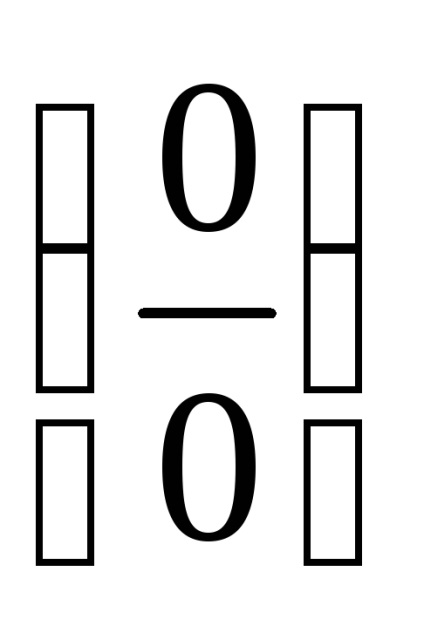
а) скористатися тотожністю, де

і- коріння рівняння, знайдені за формулою;

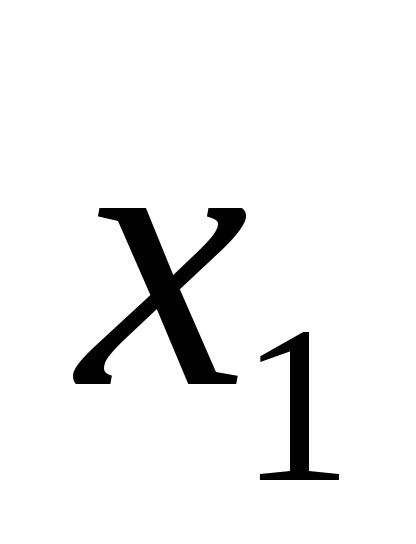
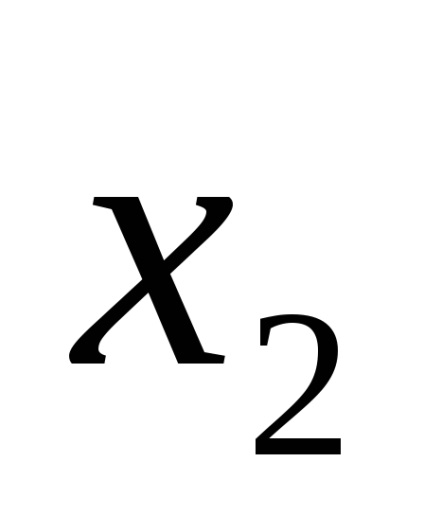
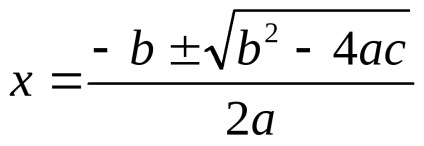
б) врахувати, що, коли, то

- один з коренів, і інший коріньможна знайти за теоремою Вієта, наприклад, з рівності, де;

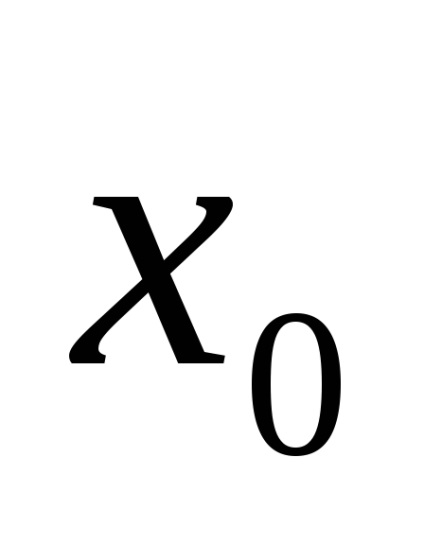
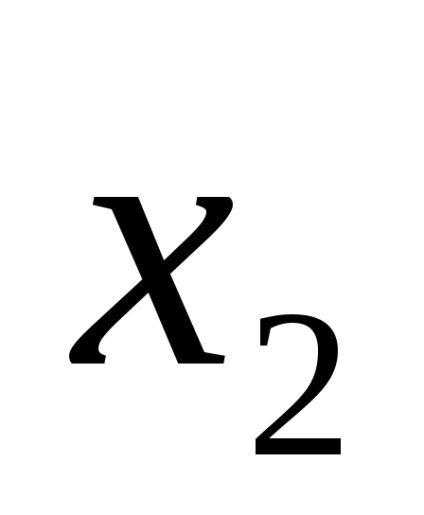
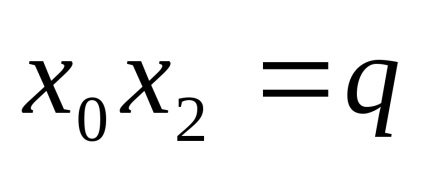
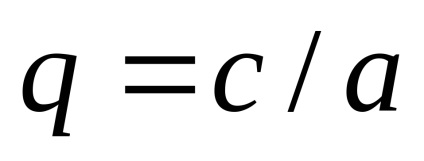
в) застосувати рівність, де

.

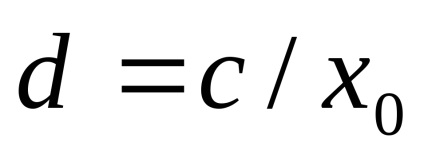
(Вирішили рівняння ії застосували 1-й спосіб).

.

У рівнянні вільний коефіцієнт -10 розділили на коефіцієнт, що стоїть перед

(Число 4). Результат розділили на відомий корінь 2. Отримали 2-й корінь.

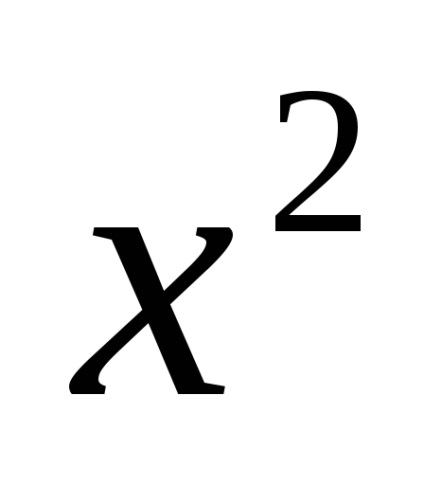
Потім в рівнянні знайшли 2-й корінь з умови

, де 2 - відомий корінь, а 6 - вільний коефіцієнт (Теорема Вієта).

.

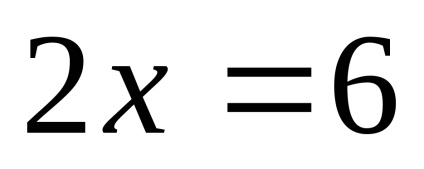
дужка

отримана як, а решта знайдені 3-м способом.

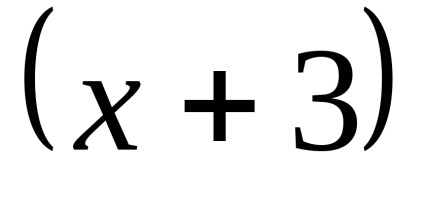
ПР6. Розкрийте невизначеність

, розклавши дріб на множники:

.

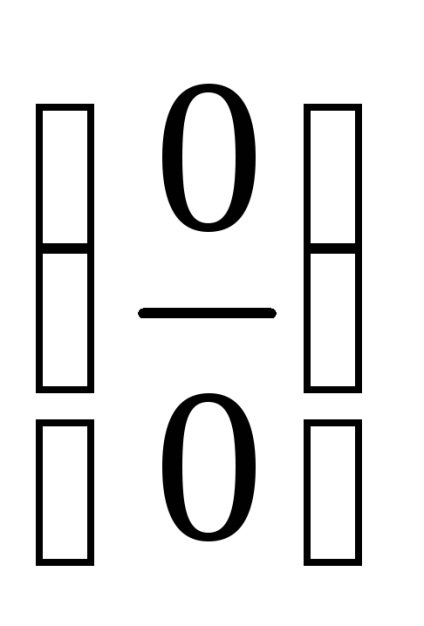
Межа дрібно-раціональної функції в нескінченності

Нехай дана функція

(Див. Стор. 16) і треба знайти. Виявляється, прився дріб поводиться так, як ставлення старших ступенів:

.

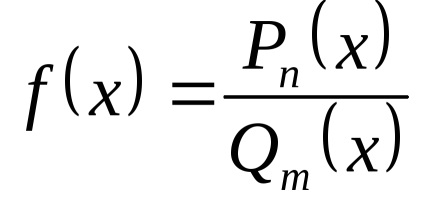
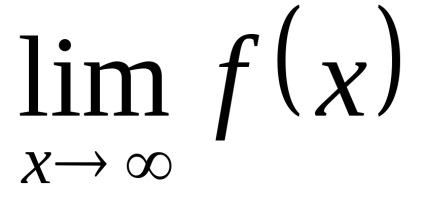
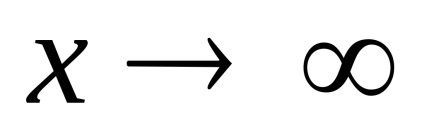
Тоді. позначимо

. Можливі 3 випадки:

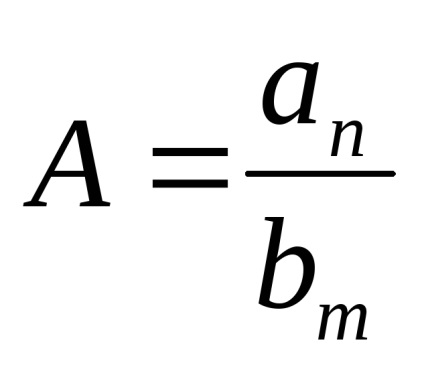
Таким чином, межа дорівнює

а) нескінченності, якщо ступінь чисельника більше, ніж ступінь знаменника;

б) 0 в протилежному випадку;

в) стосовно старших коефіцієнтів, якщо ступеня рівні.

ПР7. Знайдіть межі

ПР8. Знайдіть межі

Приклад 11. Залишивши в чисельнику і в знаменнику старші ступеня, знаходимо

Приклад 12. Залишивши старші ступеня, бачимо, що

Зверніть увагу, що знак нескінченності (якщо така виходить) у відповіді не вказується. Проте, якщо обидві старші ступеня - парні (або якщо обидві непарні), очевидно, їх ставлення завжди позитивно, що можна врахувати.

ПР9. Знайдіть межі функцій

в точках,,,,, а також при.

.

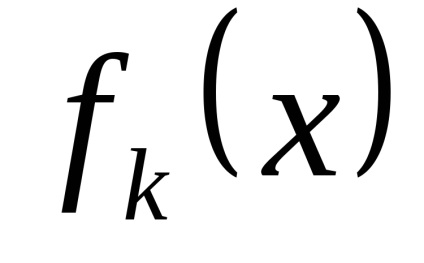
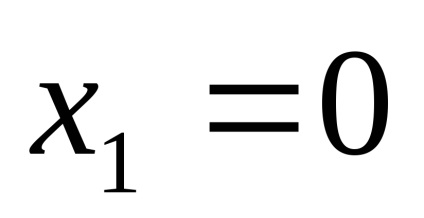
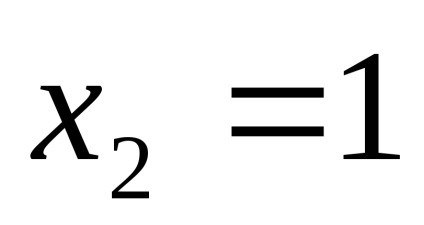
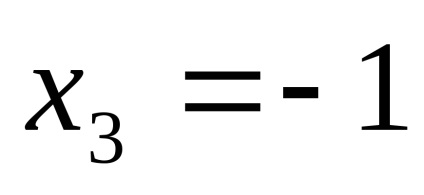
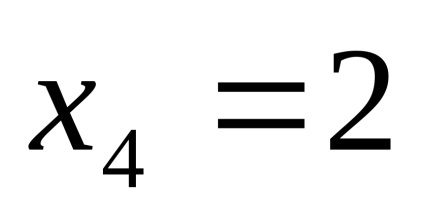
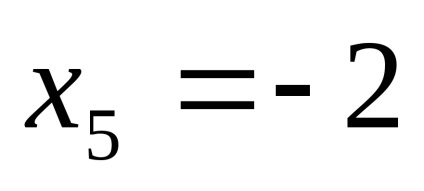
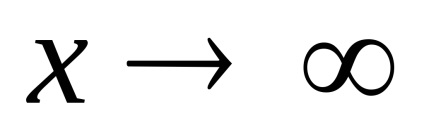
Межі ірраціональних функцій

Якщо функція містить корінь, підставляємо, як зазвичай, граничну точку. Складнощі пов'язані з невизначеністю

, коли доводиться множити чисельник і знаменник насопряжённое вираз.

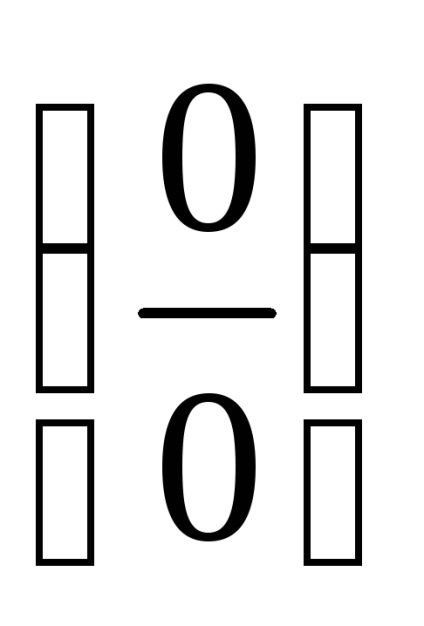
Вирази сопряжениотносітельно різниці квадратів. якщо їх твір перетворюється в різницю квадратів за формулою.

Приклади сполучених виразів

а)

пов'язане з, при цьому;

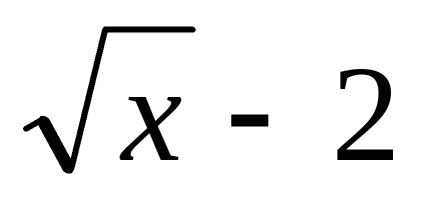
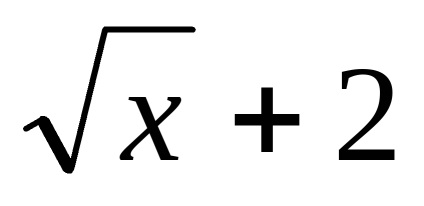
б)

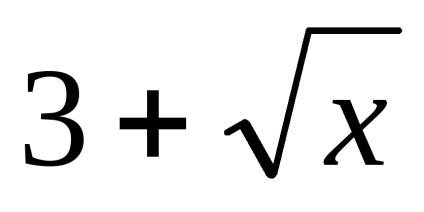
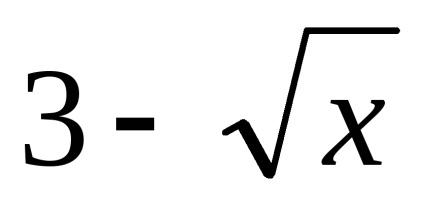
пов'язане з, і тоді;

в)

пов'язане з, оскільки

,

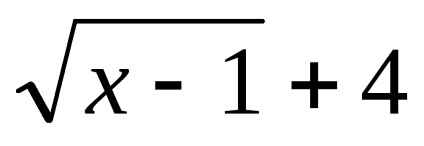
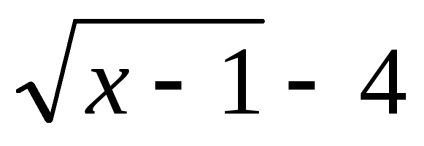
причому під коренем все залишається без змін;

.

ПР10. Знайдіть межі ірраціональних функцій простий підстановкою:

Приклад 13. Підставивши зазначені точки, знаходимо значення

ПР11. Розкрийте невизначеність

, помноживши чисельник і знаменник дробу на відповідне поєднане вираз і скоротивши однакові дужки:

.

.

.

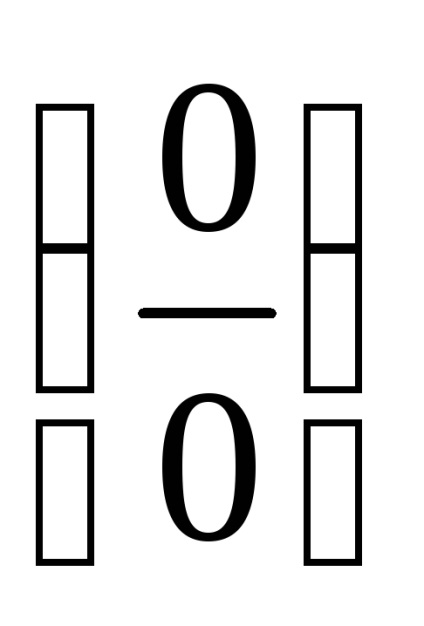
ПР12. Помножте чисельник і знаменник на вираз, поєднане до чисельника, а потім - на вираз, поєднане до знаменника. Скоротивши дужки, розкрийте невизначеність

:

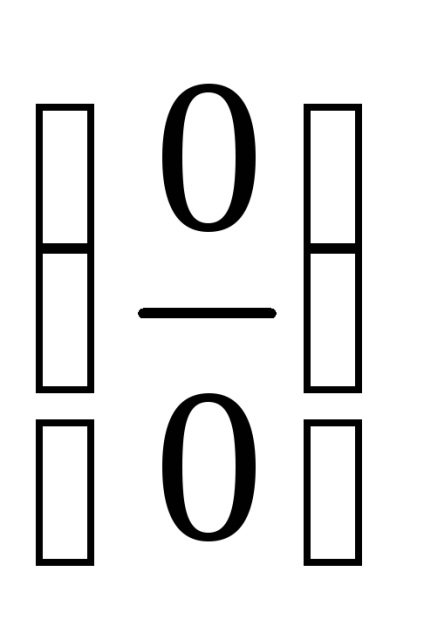
Приклад 17. Помножимо, щоб отримати різницю квадратів:

.

Приклад 18. Так само, як в прикладі 17,

.

Ірраціональні межі при

в разі невизначеностізнаходять подібно раціональним, за допомогою старших ступенів, а в разі невизначеностізводять її доза допомогою сполученого вираження.

Схожі статті

• Межа функції в нескінченності - студопедія

• Мінсільгоспу змінять назву і додадуть функцій, клуб експертів зернового ринку

• Як можна поліпшити дітородну функцію чоловіка, жіночий клуб