Для початку вам треба вміти складати СДНФ і СКНФ, тому що це, швидше за все, теж буде в контрольній. Що це таке можна прочитати і в матеріалах, і в інших доступних джерелах. Якщо коротко, то СКНФ - абсолютно кон'юнктивна нормальна форма, а СДНФ - абсолютно діз'юнктівная нормальна форма.
Абсолютно Кон'юнктивна НФ - кон'юнкція диз'юнкцій, причому в кожної диз'юнкції (в кожної дужки) присутні всі змінні, що входять в формулу, або їх заперечення, немає однакових диз'юнкцій, в кожній диз'юнкції немає однакових доданків:
Абсолютно диз'юнктивного НФ - диз'юнкція конь'юнкція. причому в кожної коньюнкции присутні всі змінні, що входять в формулу, або їх заперечення, немає однакових конь'юнкція, в кожній коньюнкции немає однакових доданків:
Тепер розглянемо приклад, в якому по таблиці істинності побудуємо СДНФ і СКНФ, а потім вже перейдемо до мінімізації.
Для прикладу візьмемо функцію з трьома змінними і вже розібрану на занятті.
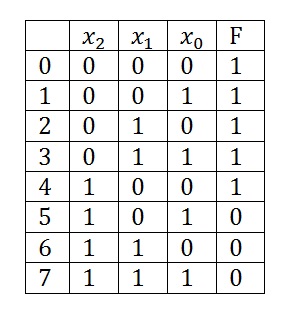
Розглянемо по пунктах, як скласти СДНФ:
1. Записуємо твір наборів змінних. якщо функція дорівнює 1 (F = 1);
2. Беремо змінну з запереченням, якщо її значення дорівнює 0
3. Між кожним твором набору змінних ставимо знак логічного додавання
Тепер складемо СДНФ для нашої таблиці істинності.
Розглянемо по пунктах, як скласти СКНФ:
1. Записуємо твір наборів змінних. якщо функція дорівнює 0 (F = 0);
2. Беремо змінну з запереченням, якщо її значення дорівнює 1;
3. Між кожним твором набору змінних ставимо знак логічного додавання
Складемо СКНФ для таблиці істинності.
Тепер перейдемо до мінімізації функцій.
Спочатку розглянемо спосіб, за допомогою якого ми буде спрощувати СДНФ і СКНФ. Почнемо з СДНФ:
Тепер шукаємо пари доданків, які відрізняються тільки однієї змінної, тобто в одному випадку вона з запереченням, в іншому - без. Виділяємо такі пари (тут такі пари будуть виділені однаковими квітами):
Але варто зауважити, що якщо розбити слоган на пари, то одне з слоган залишиться без пари. І тут ми звертаємося до аксіом алгебри логіки: Виходячи з цього, робимо наступні перетворення:
Тепер ділимо слоган на пари і виносимо за дужки однакові змінні, після чого вміст дужок скорочуються (як і чому це відбувається, ви повинні знати):
Тепер перейдемо до мінімізації СКНФ. Принцип такий же, як і з СДНФ:
Швидше за все контрольна у нас буде по СДНФ, але до СКНФ теж треба бути готовим. А тепер те, що точно буде в контрольній. Карти Карно - ще один спосіб мінімізації.
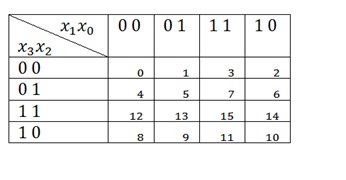
Працювати будемо вже з наявною у нас таблицею істинності. Для початку малюємо таку таблицю:
Окремо потрібно відзначити нумерацію в межах таблиці. Це вам варто запам'ятати.
Тепер заповнюємо таблицю. Відповідні клітини заповнюємо 1, якщо F = 1, і залишаємо порожніми або ставимо 0, якщо F = 0:
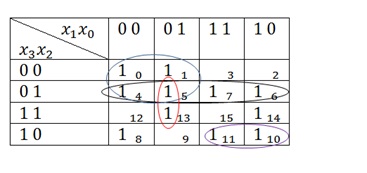
Тепер шукаємо групи сусідніх 1, які зациклюються. Сусідніми є 1, стоячи поруч один з одним по горизонталі і по вертикалі. Так само сусідніми є крайні 1, тобто 1 з клітки 0 являяется сусідній з 1 з клітки 2. Якщо важко зрозуміти, що значить «зациклюються», то можете запам'ятати, що групи одиниць можуть складатися з 2, 4, 8 і будь-якого іншого колличество одиниць рівному 2 певною мірою n. А зациклитися такі групи можуть тільки в квадраті або прямокутнику. Так само в різні групи, при необхідності, можуть потрапляти одні й ті ж 1. У кінці я розгляну її пару окремих випадків, а поки повернемося до прикладу. Отже, виділяємо групи:
Нехай група, виділена чорним, буде групою 1, а виділена червоним - групою 2. Дивимося в групах змінні, які залишаються незмінними. У групі 1 це x2, а в групі два - x1 і x0. Тепер дивимося, які значення у цих змінних: якщо 0, то беремо змінну з заперечення, якщо 1, то без. І у нас виходить наступне рівняння:
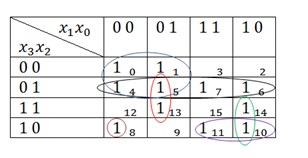
Тепер ще трохи про картах Карно. У нас в контрольних будуть функції з трьома і чотирма змінними, так що ось таблиця для чотирьох змінних, її потрібно обов'язково запам'ятати, особливо нумерацію.
А зараз на такій таблиці розглянемо ще два випадки, пов'язаних з групами з 1:
Тут майже все 1 віднесені до груп. Залишився тільки 1 з клітин 14 і 8. Спочатку подивимося на 1 в клітці 14. Вона сусідніх з 1 з клітин 6 і 10. Але, як ми уще знаємо, не можна робити групу з трьох 1. Отже, можна об'єднати ту 1 до групи з 1 або з клітки 6, або з клітки 10. і то, і то буде вірно. Але не можна об'єднувати 1 і з 1 з клітки 6, і з клітки 10. Тобто або так:
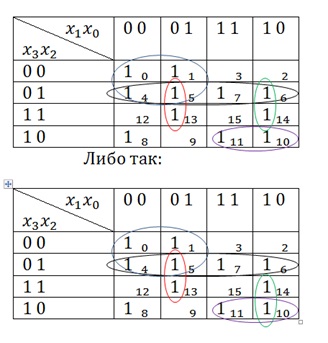
Залишилася 1 в клітці 8. Тут все просто. Якщо 1 ні з ким зациклити, то вона зациклюється сама на себе. Виглядати це буде так:
Ну, начебто, все. Будуть питання, звертайтесь. Успіхів всім на контрольній!